Правила дифференцирования (f(x)+g(x))΄ и (c f(x))΄ Решение задач 11 класс

«Правила дифференцирования (f(x)+g(x))΄ и (c f(x))΄»
Решение задач
11 класс

Цели урока
Ввести правила дифференцирования (f(x)+g(x))΄ и (c f(x))΄
Учиться применять новое знание при решении задач

Этапы урока
Проверочная работа
Изучение нового материала
Решение задач
Самостоятельная работа
Подведение итогов

Прототип задания B8 (№ 119976)

Прототип задания B8 (№ 123717)

Выведем формулу (f(x)+g(x))΄
f(x)
g(x)
g(x + h)
3 шаг.
Аналогично можно доказать, что производная суммы (разности) нескольких функций равна ……… (…………) производных этих функций.
g(x + h)
g’(x)
g’(x)
суммe разности

Правила дифференцирования:
=
=
I. Определение.
II. Формулы и правила.
Формулы (частные случаи):
Формулы (степенная функция):
Производная

Опорный конспект

Решить задачу
Найти скорость движения в момент времени t = 7, если S (t) = t² + t.

Решить задачу
Материальная точка движется
прямолинейно по закону ,
где — расстояние от точки отсчета в метрах, — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t=6 с.

Найти производную функции
a)
b)

Прототип задания B8 (№ 123717)

План решения
Найти зависимость скорости от времени (x‘(t))
Найти момент времени, в который скорость равна заданной величине (решить уравнение x’(t)=v)

Самостоятельная работа
1Вариант - задание B8 (№ 123717)
Материальная точка движется прямолинейно по закону
где — расстояние от точки отсчета в метрах, — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 1 м/с?
2 Вариант - задание B8 (№ 123719)
Материальная точка движется прямолинейно по закону
где — расстояние от точки отсчета в метрах, — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 93 м/с?

– п.к.
– п.к.
Ответ: 1 с
Ответ: 5 с

Домашнее задание
§ 46 (таблица)
№ 802, 803, 805, 810,818 (ч);
выполнить два известных задания В8 (новым способом).

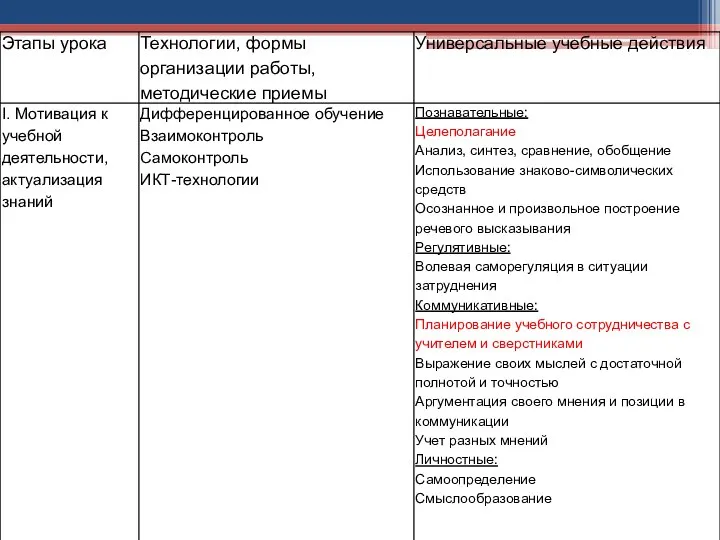
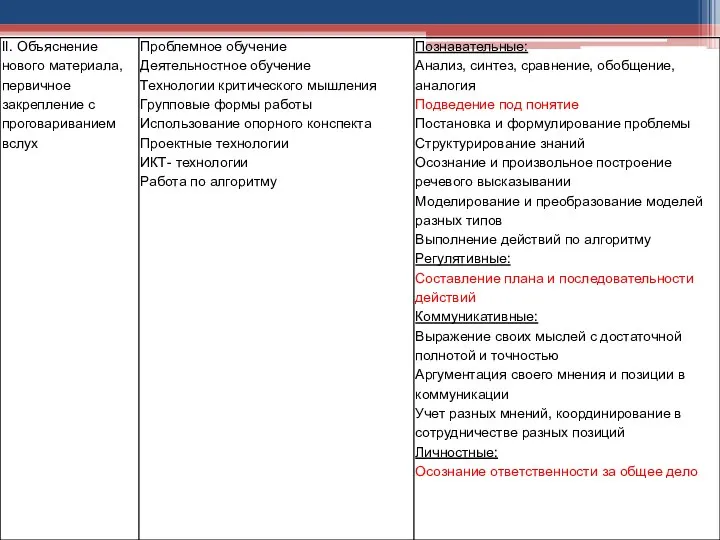
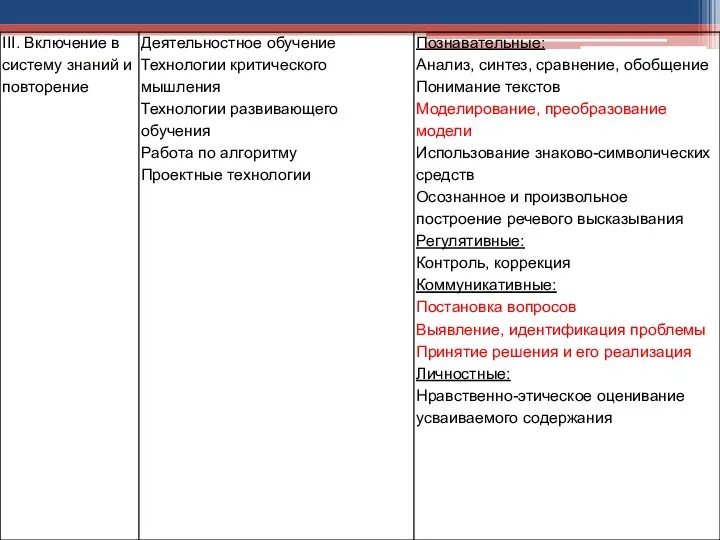
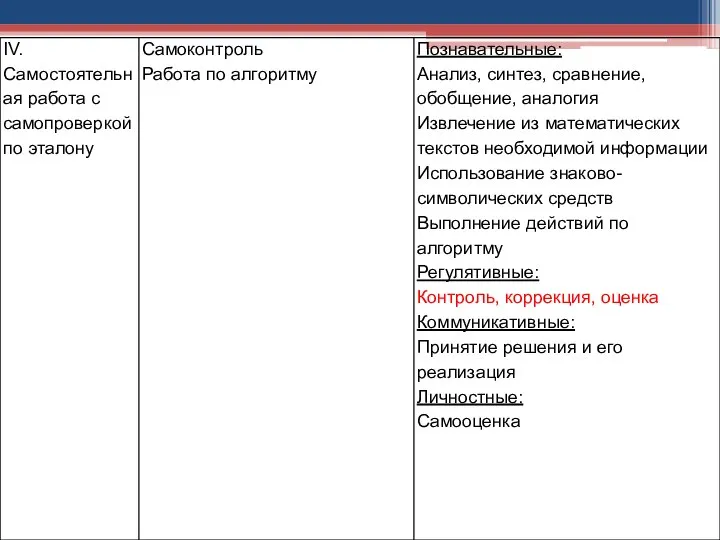
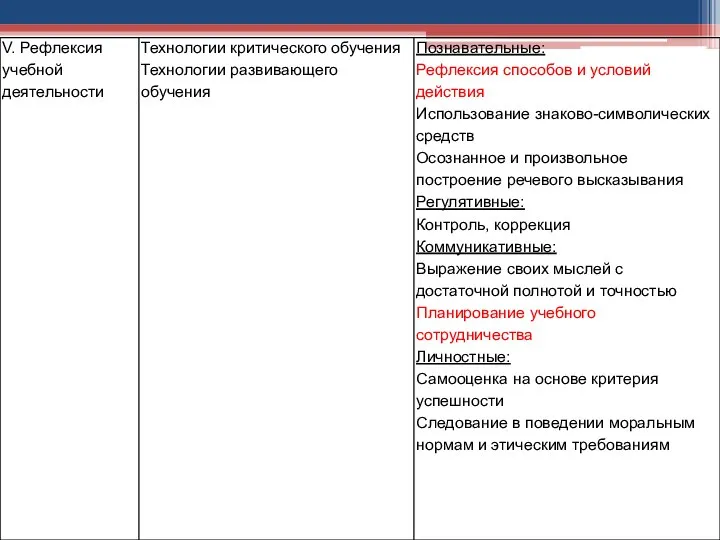
Используемые на уроке: технологии, формы организации работы, методические приемы, как средства формирования УУД