Правильные многогранники

Запишите тему, ознакомьтесь с презентацией и письменно ответьте на вопросы:
Правильный многогранник(понятие) без рисунка
Названия, с определениями, рисунки только к трем.
Как называются невыпуклые правильные многогранники?
Приведите 2-3 примера, правильных многогранников в природе.
Выполните тест(только ответы)

Правильным называется многогранник, у которого все грани являются правильными многоугольниками, и все многогранные углы при вершинах равны.
Приведён пример правильного многогранника (икосаэдр), его гранями являются правильные (равносторонние) треугольники.

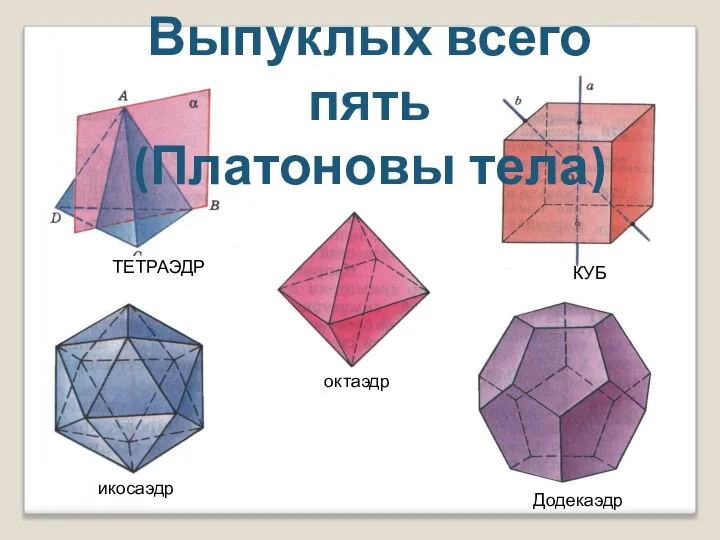
Выпуклых всего пять
(Платоновы тела)
ТЕТРАЭДР
КУБ
октаэдр
икосаэдр
Додекаэдр

Правильный многогранник, у которого грани правильные треугольники и в каждой вершине сходится по три ребра и по три грани. У тетраэдра: 4 грани, четыре вершины и 6 ребер.
Тетраэдр

Правильный многогранник, у которого грани- правильные треугольники и в каждой вершине сходится по четыре ребра и по четыре грани. У октаэдра: 8 граней, 6 вершин и 12 ребер
Октаэдр

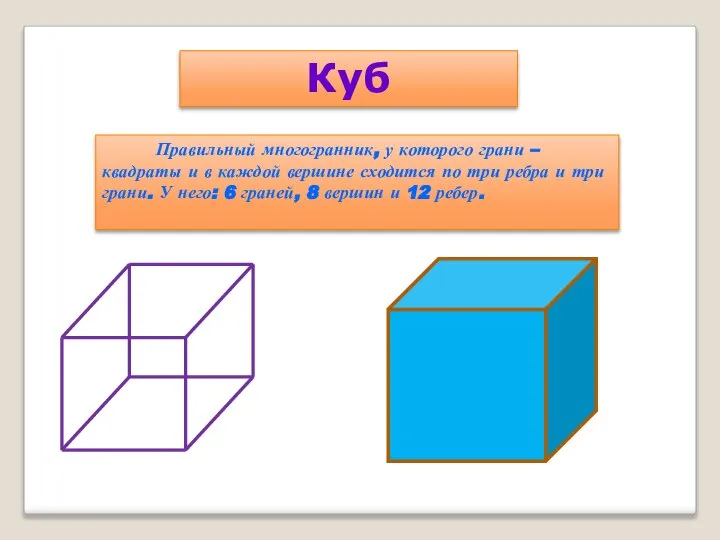
Правильный многогранник, у которого грани – квадраты и в каждой вершине сходится по три ребра и три грани. У него: 6 граней, 8 вершин и 12 ребер.
Куб

Додекаэдр
Правильный многогранник, у которого грани правильные пятиугольники и в каждой вершине сходится по три ребра и три грани. У додекаэдра:12 граней, 20 вершин и 30 ребер.

ИКОСАЭДР
Правильный многогранник, у которого грани правильные треугольники и в каждой вершине сходится по пять ребер и пять граней. У икосаэдра :20 граней, 12 вершин и 30 ребер.

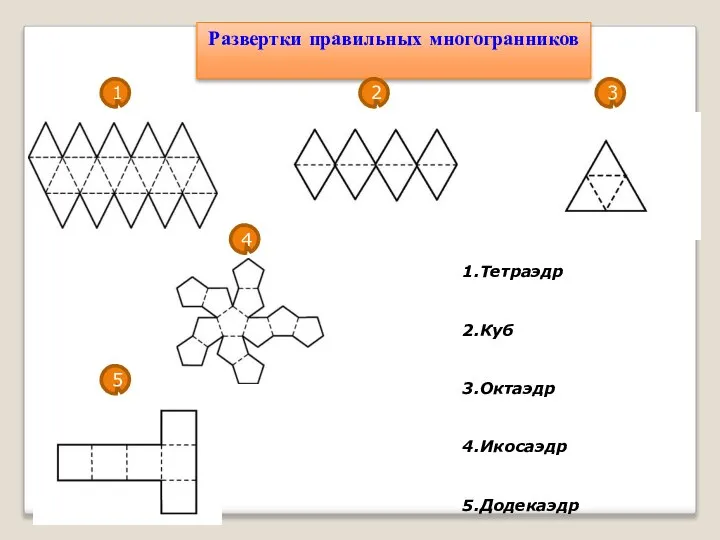
Развертки правильных многогранников
1.Тетраэдр
2.Куб
3.Октаэдр
4.Икосаэдр
5.Додекаэдр
1
2
3
4
5

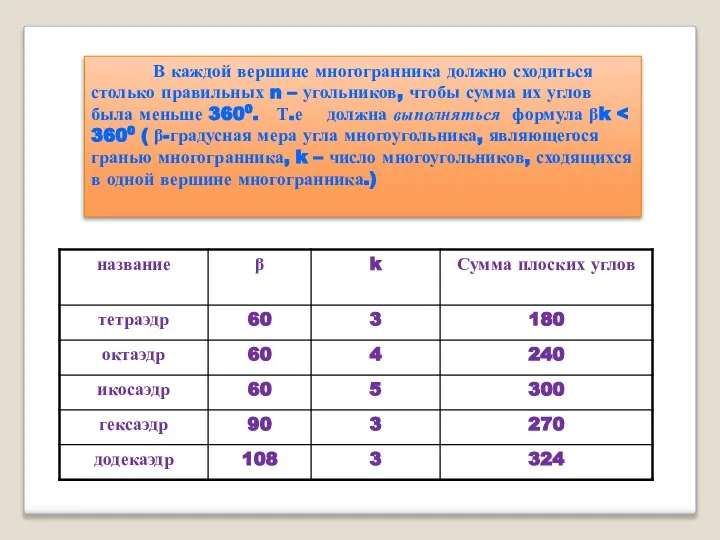
В каждой вершине многогранника должно сходиться столько правильных n – угольников, чтобы сумма их углов была меньше 3600. Т.е должна выполняться формула βk < 3600 ( β-градусная мера угла многоугольника, являющегося гранью многогранника, k – число многоугольников, сходящихся в одной вершине многогранника.)

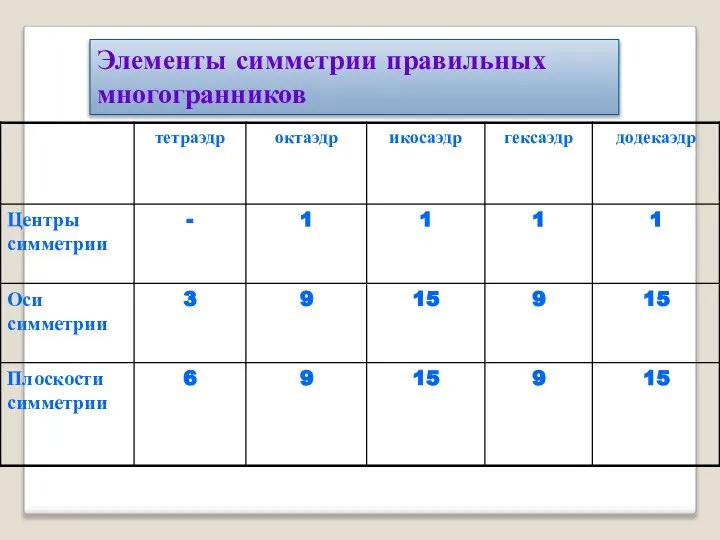
Элементы симметрии правильных многогранников

Все типы правильных многогранников были известны в Древней Греции – именно им посвящена завершающая, XIII книга «Начал» Евклида.
Немного истории

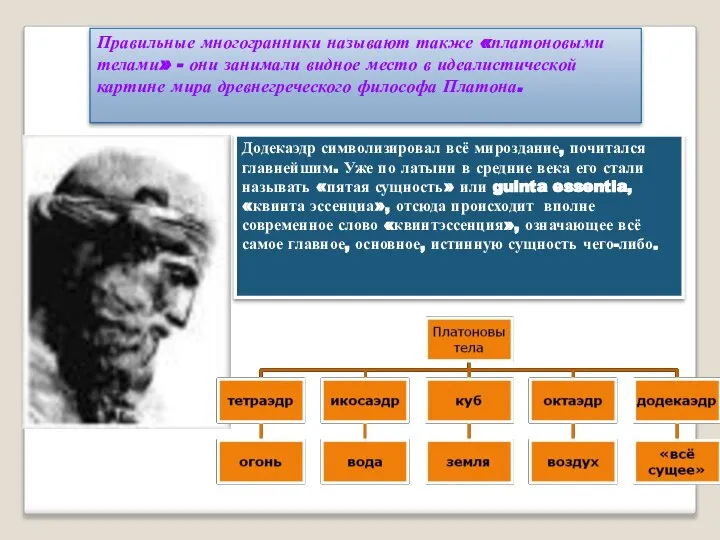
Правильные многогранники называют также «платоновыми телами» - они занимали видное место в идеалистической картине мира древнегреческого философа Платона.
Додекаэдр символизировал всё мироздание, почитался главнейшим. Уже по латыни в средние века его стали называть «пятая сущность» или guinta essentia, «квинта эссенциа», отсюда происходит вполне современное слово «квинтэссенция», означающее всё самое главное, основное, истинную сущность чего-либо.

За каждым, в древности, закрепили стихии(огонь, воздух, вода, земля, вселенная)

Звездчатые, не выпуклые, правильные многогранники:

.
Существует семейство тел, родственных платоновым - это полуправильные выпуклые многогранники, или Архимедовы тела. У них все многогранные углы равны, все грани - правильные многоугольники, но нескольких различных типов.

Некоторые из правильных и полуправильных тел встречаются в природе в виде кристаллов, другие — в виде вирусов, простейших микроорганизмов.
Кристаллы — тела, имеющие многогранную форму. Вот один из примеров таких тел: кристалл пирита (сернистый колчедан FeS) — природная модель додекаэдра. Пирит (от греч. “пир” — огонь) — сернистое железо или серный колчедан, наиболее распространенный минерал из группы сульфидов. Размеры кристаллов пирита часто достигают нескольких сантиметров и являются хорошим коллекционным материалом. От других подобных ему минералов отличается твердостью: царапает стекло.

Замечено, что наша матушка-Земля последовательно проходит эволюцию правильных объемных фигур. Существует много данных о сравнении структур и процессов Земли с вышеуказанными фигурами. Полагают, что четырем геологическим эрам Земли соответствуют четыре силовых каркаса правильных Платоновских тел: Протозою - тетраэдр (четыре плиты), Палеозою - гексаэдр (шесть плит) ,Мезозою - октаэдр (восемь плит) ,Кайнозою - додекаэдр (двенадцать плит).
Существует гипотеза, по которой ядро Земли имеет форму и свойства растущего кристалла, оказывающего воздействие на развитие всех природных процессов, идущих на планете. «Лучи» этого кристалла, а точнее его силовое поле, обусловливают икосаэдро-додекаэдрическую структуру Земли, проявляющуюся в том, что в земной коре как бы проступают проекции вписанных в земной шар правильных многогранников: икосаэдра и додекаэдра. 62 их вершины и середины ребер, называемые узлами, оказывается, обладают рядом специфичecких свойств, позволяющих объяснить многие непонятные явления.

Если нанести на глобус очаги наиболее крупных и примечательных культур и цивилизаций Древнего мира, можно заметить закономерность в их расположении относительно географических полюсов и экватора планеты. Многие залежи полезных ископаемых тянутся вдоль икосаэдрово-додекаэдровой сетки. Еще более удивительные вещи происходят в местах пересечения этих ребер: тут располагаются очаги древнейших культур и цивилизаций: Перу, Северная Монголия, Гаити, Обская культура и другие. В этих точках наблюдаются максимумы и минимумы атмосферного давления, гигантские завихрения Мирового океана, здесь шотландское озеро Лох-Несс, Бермудский треугольник. Дальнейшие исследования Земли, возможно, определят отношение к этой красивой научной гипотезе, в которой, как видно, правильные многогранники занимают важное место.

Додекаэдрическая структура, по мнению Д. Винтера (американского математика), присуща не только энергетическому каркасу Земли, но и строению живого вещества.
В процессе деления яйцеклетки сначала образуется тетраэдр из четырех клеток, затем октаэдр, куб и, наконец, додекаэдро-икосаэдрическая структура гаструлы. И наконец, самое, пожалуй, главное – структура ДНК генетического кода жизни – представляет собой четырехмерную развертку (по оси времени) вращающегося додекаэдра! Таким образом, оказывается, что вся Вселенная – от Метагалактики и до живой клетки – построена по одному принципу – бесконечно вписываемых друг в друга додекаэдра и икосаэдра, находящихся между собой в пропорции золотого сечения!

Впрочем, многогранники - отнюдь не только объект научных исследований. Их формы - завершенные и причудливые, широко используются в декоративном искусстве.

Ярчайшим примером художественного изображения многогранников в XX веке являются, конечно, графические фантазии Маурица Корнилиса Эшера (1898-1972), голландского художника, родившегося в Леувардене.
Мауриц Эшер в своих рисунках как бы открыл и интуитивно проиллюстрировал законы сочетания элементов симметрии, т.е. те законы, которые властвуют над кристаллами, определяя и их внешнюю форму, и их атомную структуру, и их физические свойства.
Математик, так же как и художник или поэт, создает узоры, и если
его узоры более устойчивы, то лишь потому, что они составлены из идей.

Тест
1. Многогранник, составленный из четырех правильных многоугольников:
А) Тетраэдр В) Куб С) Октаэдр D) Икосаэдр Е) Додекаэдр
2. Многогранник, составленный из пятиугольников:
А) Тетраэдр В) Куб С) Октаэдр D) Икосаэдр Е) Додекаэдр
3. Многогранник, составленный из восьми треугольников:
А) Тетраэдр В) Куб С) Октаэдр D) Икосаэдр Е) Додекаэдр

Тест (продолжение)
4. Многогранник, каждая вершина которого является вершиной пяти треугольников:
А) Тетраэдр В) Куб С) Октаэдр D) Икосаэдр Е) Додекаэдр
5. Многогранник, каждая вершина которого является вершиной трех квадратов:
А) Тетраэдр В) Куб С) Октаэдр D) Икосаэдр Е) Додекаэдр
6. Многогранник с восьмью гранями:
А) Тетраэдр В) Куб С) Октаэдр D) Икосаэдр Е) Додекаэдр
7. Многогранник, с четырьмя гранями:
А) Тетраэдр В) Куб С) Октаэдр D) Икосаэдр Е) Додекаэд