Слайд 2Правила построения сечений многогранников:
1) проводим прямые через точки, лежащие в одной плоскости;
2)

ищем прямые пересечения плоскости сечения с гранями многогранника, для этого
а) ищем точки пересечения прямой принадлежащей плоскости сечения с прямой, принадлежащей одной из граней (лежащие в одной плоскости);
б) параллельные грани плоскость сечения пересекает по параллельным прямым.
Слайд 3Примеры построения сечений:
Пример 1.
Рассмотрим прямоугольный параллелепипед ABCDA1B1C1D1. Построим сечение, проходящее через точки

M, N, L
Слайд 4Соединим точки M и L, лежащие в плоскости AA1D1D

Слайд 5Пересечем прямую ML
(принадлежащую сечению) с ребром A1D1, они лежат в одной

плоскости AA1D1D. Получим точку X1.
Слайд 6Точка X1 лежит на ребре A1D1, а значит и плоскости A1B1C1D1, соединим ее

сточкой N, лежащей в этой же плоскости.
X1 N пересекается с ребром A1B1 в точке К.
Слайд 7Соединим точки K и M, лежащие в одной плоскости AA1B1B

Слайд 8Найдем прямую пересечения плоскости сечения с плоскостью DD1C1C:
пересечем прямую ML (принадлежащую сечению)

с ребром DD1, они лежат в одной плоскости AA1D1D, получим точку X2
Слайд 9пересечем прямую KN (принадлежащую сечению) с ребром D1C1, они лежат в одной

плоскости A1B1C1D1, получим точку X3
Слайд 10Точки X2 и X3 лежат в плоскости DD1C1C. Проведем прямую X2 X3

, которая пересечет ребро C1C в точке T, а ребро DC в точке P. И соединим точки L и P, лежащие в плоскости ABCD
MKNTPL - искомое сечение
Слайд 11Пример 2
Рассмотрим ту же самую задачу на построение сечения, но воспользуемся свойством

параллельных плоскостей. Это облегчит нам построение сечения
Слайд 12Соединим точки M и L, лежащие в плоскости AA1D1D

Слайд 13Через точку N, проведем прямую NT параллельную прямой ML. Прямые NT и

ML лежат в параллельных плоскостях по свойству параллелепипеда
Слайд 14Пересечем прямую ML (принадлежащую сечению) с ребром A1D1, они лежат в одной

плоскости AA1D1D. Получим точку X1
Слайд 15Точка X1 лежит на ребре A1D1, а значит и плоскости A1B1C1D1, соединим

ее сточкой N, лежащей в этой же плоскости.
X1 N пересекается с ребром A1B1 в точке К
Слайд 16Соединим точки K и M, лежащие в одной плоскости AA1B1B

Слайд 17Проведем прямую TP через точку T, параллельно прямой KM ( они лежат

в параллельных плоскостях)
















 Ознакомление с задачей в 2 действия
Ознакомление с задачей в 2 действия Решение задач. Самостоятельная работа (ЕГЭ)
Решение задач. Самостоятельная работа (ЕГЭ) Аксиомы стереометрии. Взаимное расположение прямых и плоскостей в пространстве
Аксиомы стереометрии. Взаимное расположение прямых и плоскостей в пространстве Метод координат на плоскости
Метод координат на плоскости Иррациональные уравнения. Задания для устного счета
Иррациональные уравнения. Задания для устного счета Устные упражнения. Выразите в процентах
Устные упражнения. Выразите в процентах Стереометрия. Метод координат в задачах ЕГЭ
Стереометрия. Метод координат в задачах ЕГЭ Задание 19. Профиль (1)
Задание 19. Профиль (1) Переменные величины и их свойства
Переменные величины и их свойства Линейная алгебра. (Матрицы, определители)
Линейная алгебра. (Матрицы, определители) Презентация на тему Формулы сокращенного умножения. Представление выражения в виде многочлена
Презентация на тему Формулы сокращенного умножения. Представление выражения в виде многочлена  Динамическое программирование
Динамическое программирование Задачи на нахождение неизвестного
Задачи на нахождение неизвестного Решаем задачу
Решаем задачу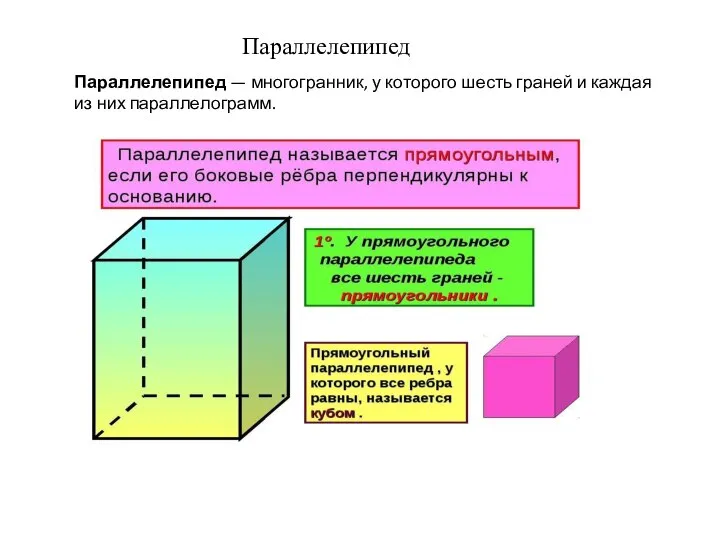 Параллелепипед
Параллелепипед Пирамида
Пирамида Решение задач с помощью систем уравнений (часть 2)
Решение задач с помощью систем уравнений (часть 2) Число и цифра 6. 1 класс
Число и цифра 6. 1 класс Задания 15 и 4
Задания 15 и 4 Прямой угол
Прямой угол Логарифмические уравнения и неравенства
Логарифмические уравнения и неравенства Функции, их свойства и графики
Функции, их свойства и графики Множественные связи. Порядковые и категоризованные переменные
Множественные связи. Порядковые и категоризованные переменные Уравнение сферы
Уравнение сферы Геометрический и физический смысл производной
Геометрический и физический смысл производной Площадь параллелограмма
Площадь параллелограмма Изображение фигур в пространстве
Изображение фигур в пространстве Решение тригонометрических уравнений и их систем
Решение тригонометрических уравнений и их систем