Предел функции. Раскрытие неопределенности

Свойства вычисления пределов
Если lim хn = b и lim уn = c , то
n→∞ n→∞
1)Предел суммы равен сумме пределов:
lim (хn+ уn) = lim хn + lim уn = b + c
n→∞ n→∞ n→∞
2)Предел произведения равен произведению пределов:
lim (хn· уn) = lim хn ∙ lim уn = b · c
n→∞ n→∞ n→∞
3)Предел частного равен частному пределов:
lim (хn : уn) = lim хn : lim уn = b : c
n→∞ n→∞ n→∞
4)Постоянный множитель можно вынести за знак предела:
lim (k · хn) = k · lim хn = k ∙ b
n→∞ n→∞

Правила вычисления пределов
1. Если старшая степень числителя и знаменателя совпадают, то предел такого вида всегда будет равен отношению коэффициентов при старших степенях переменной.

Правила вычисления пределов
2. Если степень знаменателя выше степени числителя, то предел такого вида равен нулю.

Правила вычисления пределов
3. Если же старшая степень числителя выше степени знаменателя, то, очевидно, все слагаемые знаменателя в пределе будут равны нулю, это означает, что предел не существует.

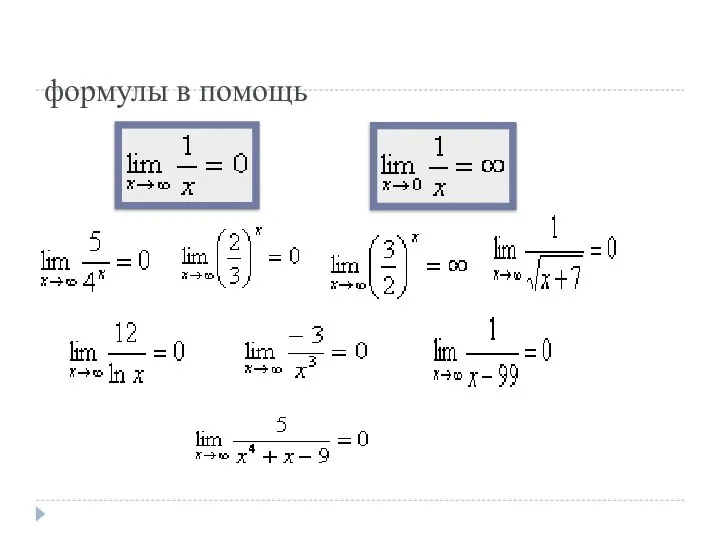
формулы в помощь

Методика вычисления пределов в точке

Раскрытие неопределенности вида 0/0
Вычислить предел
Сначала попробуем подставить -1 в дробь:
В данном случае получена так называемая неопределенность 0/0
Общее правило: если в числителе и знаменателе находятся многочлены, и имеется неопределенность вида 0/0, то для ее раскрытия нужно разложить числитель и знаменатель на множители.
Очевидно, что можно сократить на (х+1)
:
Теперь и подставляем -1 в выражение, которое осталось под знаком предела:

Пример 1. Вычислить

Пример 2. Вычислить