Содержание
- 2. Картина Рафаэля «Афинская школа». На ней изображены Пифагор, Евклид, Платон и другие основоположники геометрии, а вокруг
- 3. «Необученным геометрии вход воспрещён» Научная школа Платона (открыта в 387 г. до н.э.) – Академия –
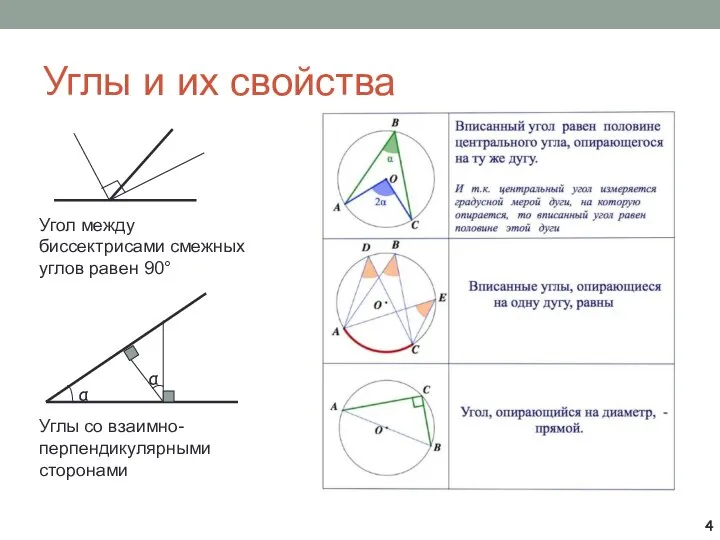
- 4. Углы и их свойства Угол между биссектрисами смежных углов равен 90° Углы со взаимно-перпендикулярными сторонами
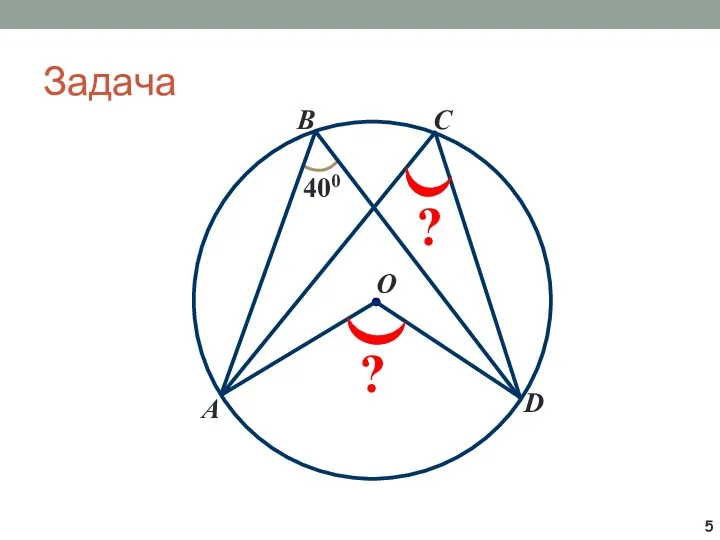
- 5. Задача
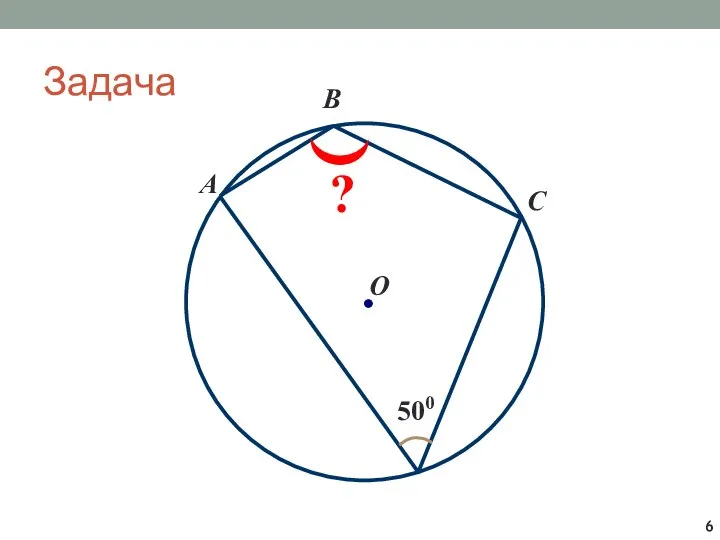
- 6. Задача
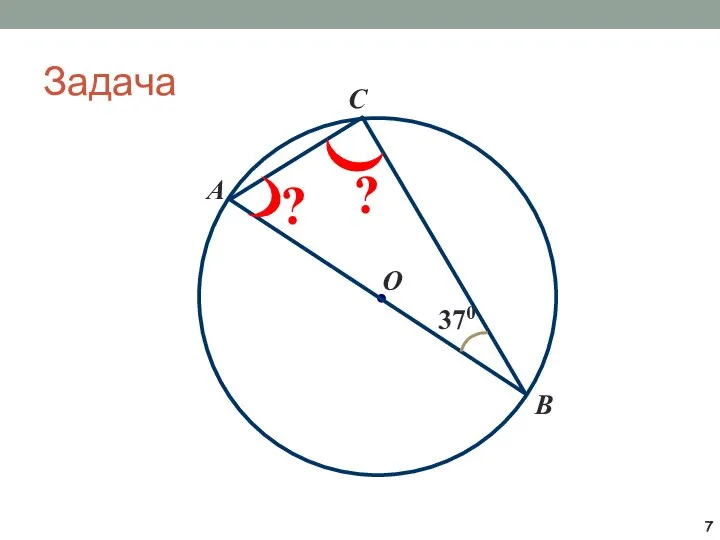
- 7. Задача
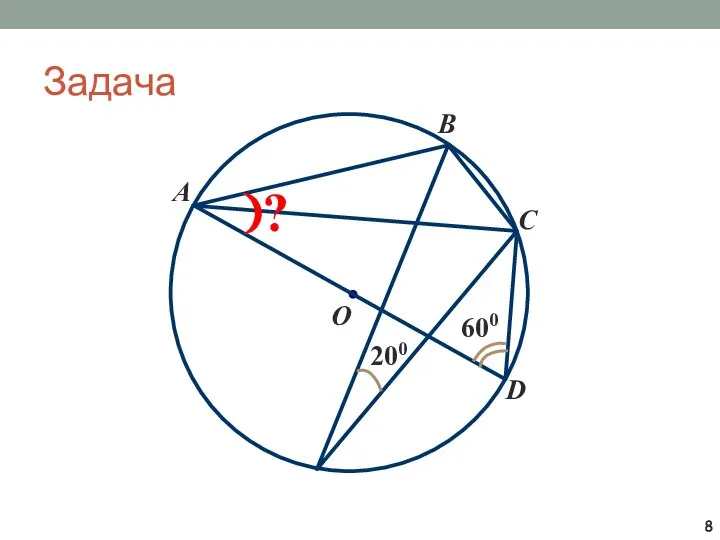
- 8. Задача
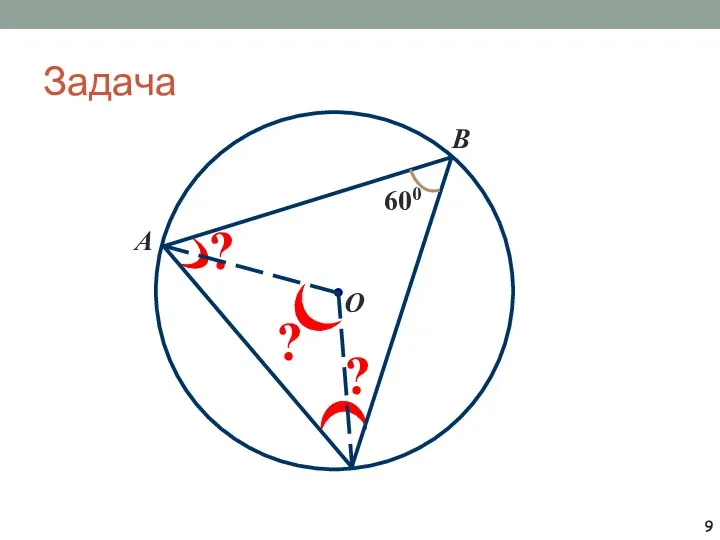
- 9. Задача
- 10. Параллельные прямые a||b, c - секущая соответственные углы (4 и 5; 6 и 7; 1 и
- 11. Треугольники Первый признак равенства треугольников Если две стороны и угол, заключенный между ними, одного треугольника соответственно
- 12. Треугольники Сумма углов треугольника равна 180° Неравенство треугольника: Центр вписанной окружности равноудалён от всех сторон и
- 13. Площадь треугольника ha
- 14. Подобие треугольников I признак подобия треугольников. Если два угла одного треугольника соответственно равны двум углам другого,
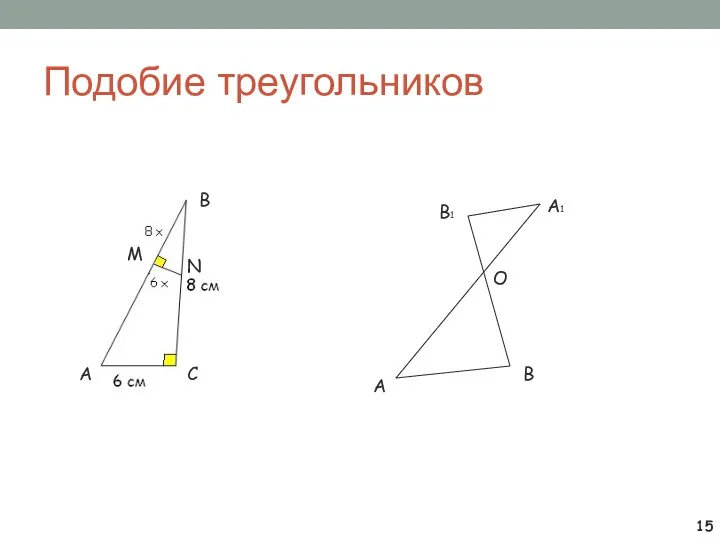
- 15. Подобие треугольников B A C M N A A1 B B1 O
- 16. Прямоугольный треугольник Против угла в 30° лежит катет, равный половине гипотенузы
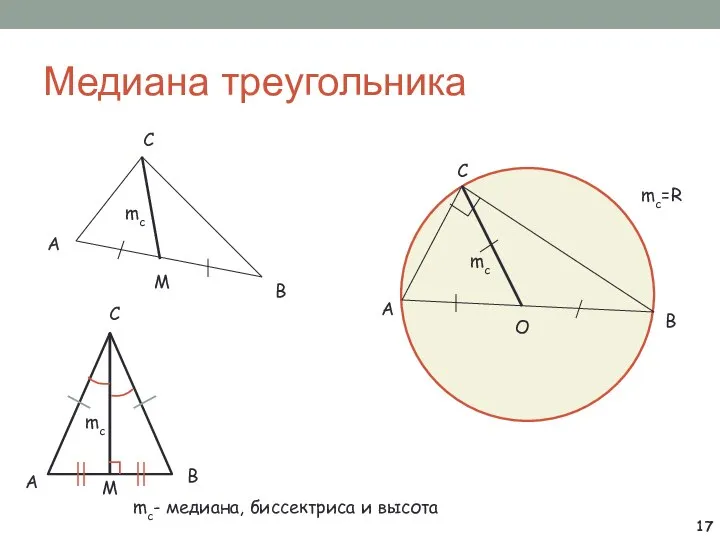
- 17. Медиана треугольника А В С М mc А В С О mc=R mc А С В
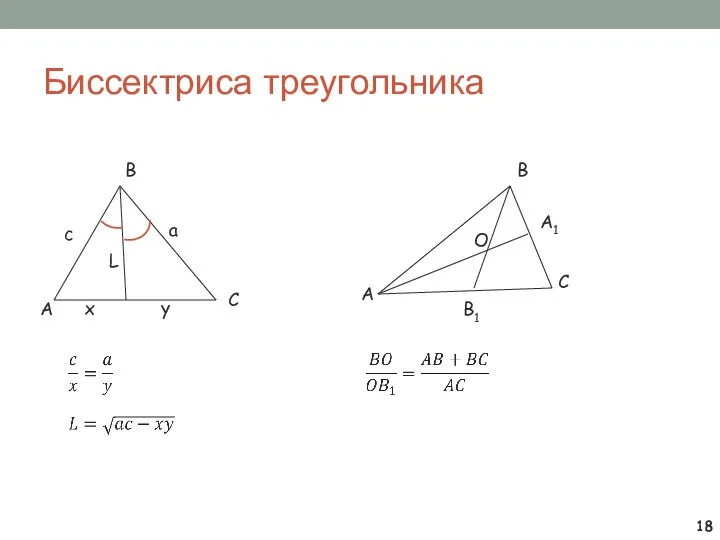
- 18. Биссектриса треугольника L A В С а с х у А В С В1 А1 О
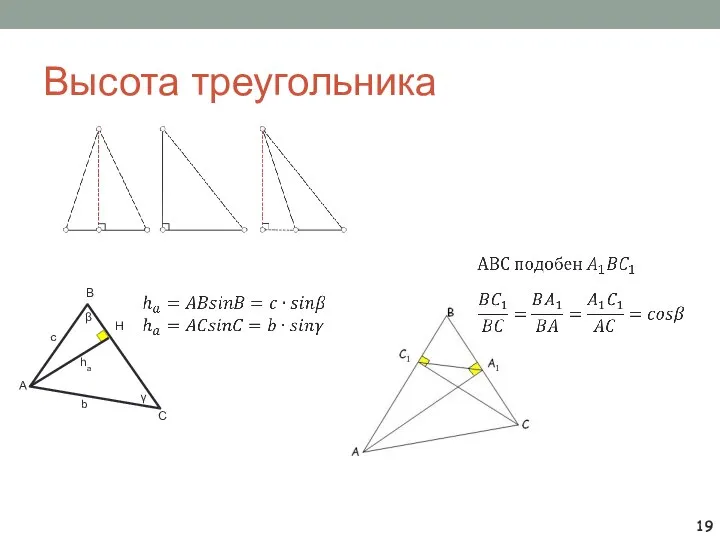
- 19. Высота треугольника A B C H ha c b β γ
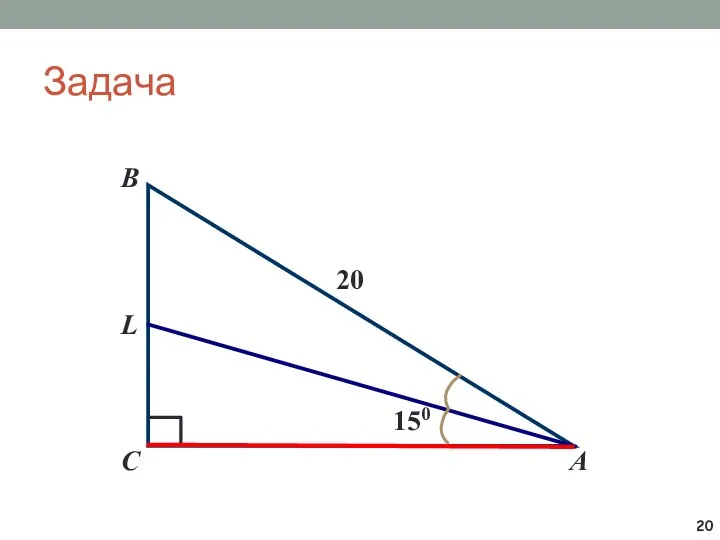
- 20. Задача
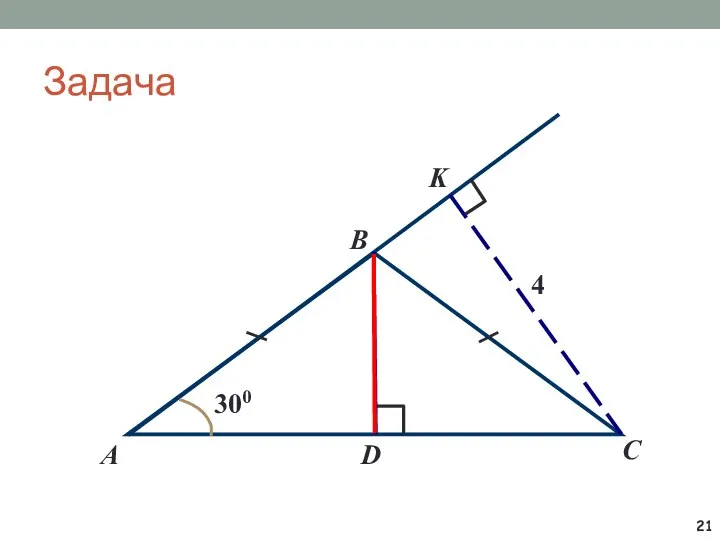
- 21. Задача
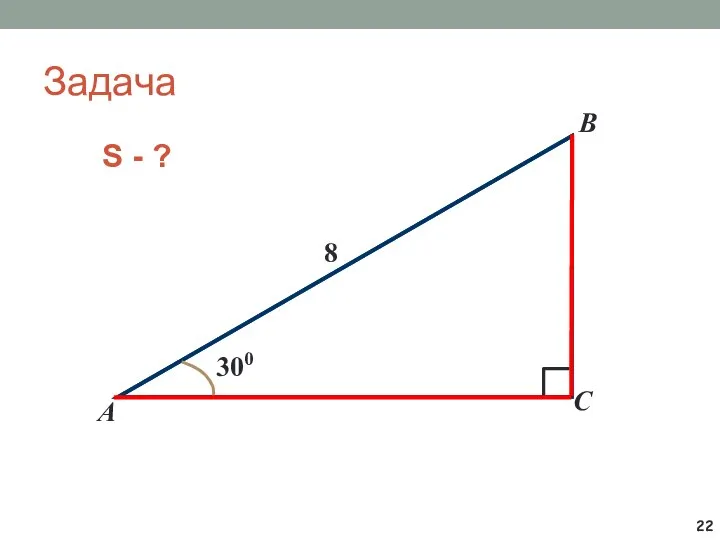
- 22. Задача B А C 8 300 S - ?
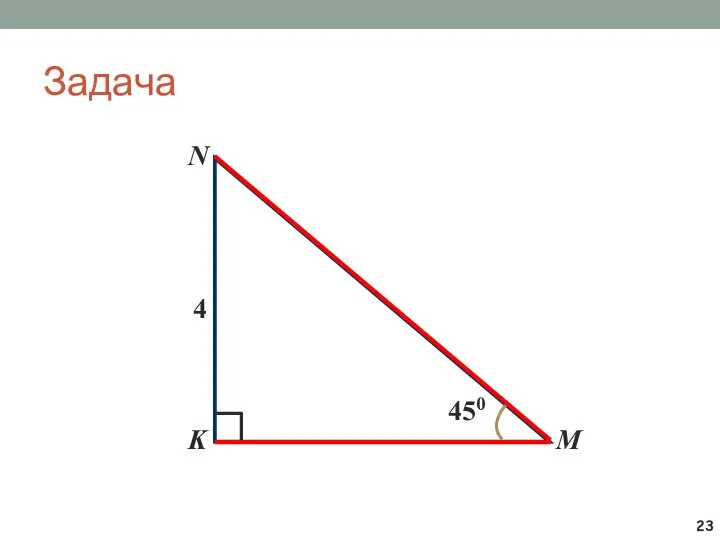
- 23. Задача
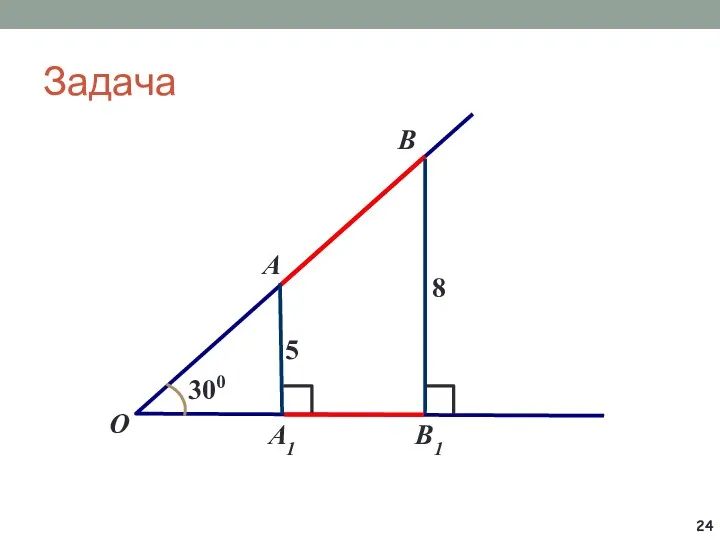
- 24. Задача
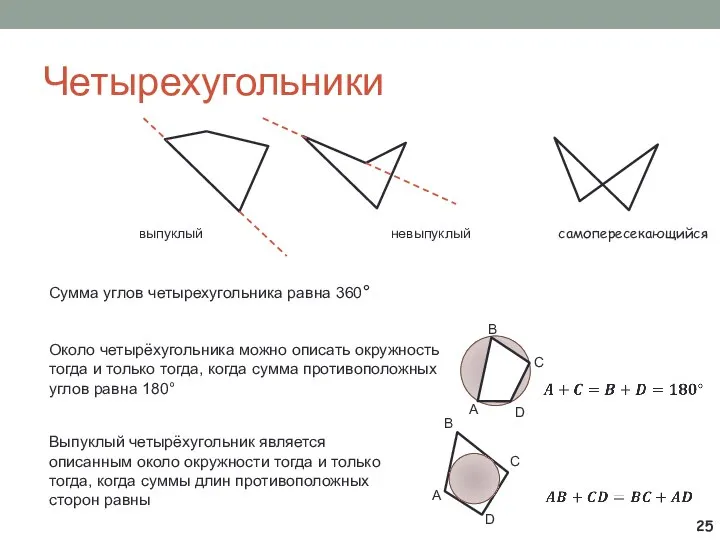
- 25. Четырехугольники невыпуклый выпуклый самопересекающийся Сумма углов четырехугольника равна 360° Около четырёхугольника можно описать окружность тогда и
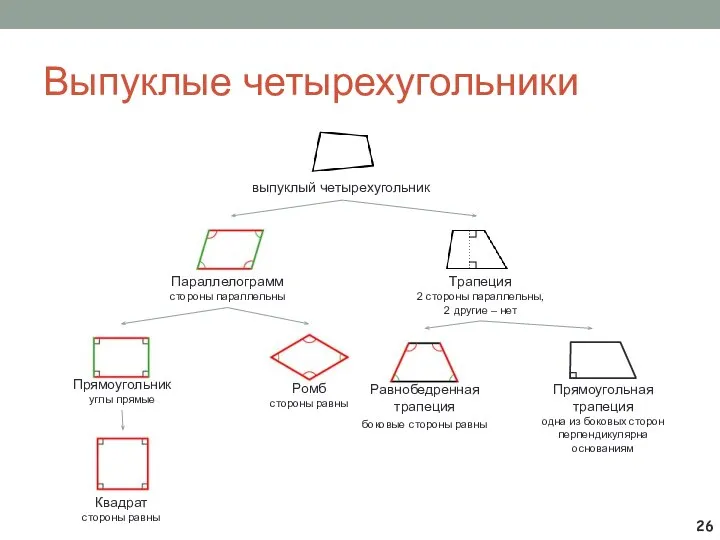
- 26. Выпуклые четырехугольники выпуклый четырехугольник Параллелограмм стороны параллельны Трапеция 2 стороны параллельны, 2 другие – нет Прямоугольник
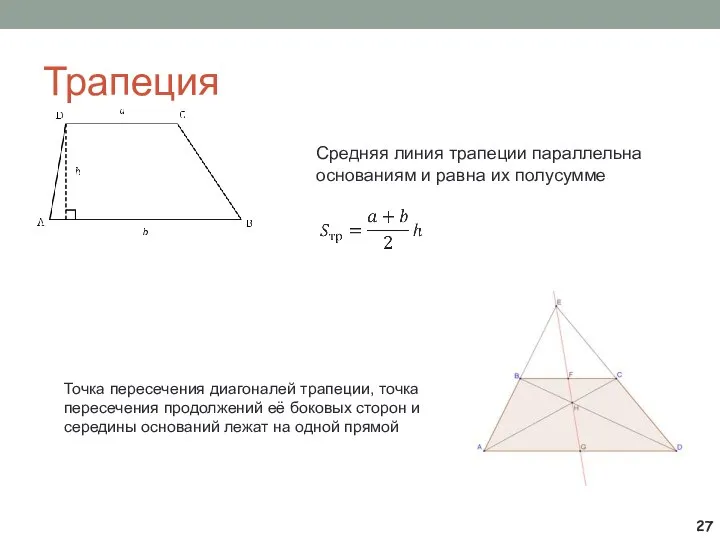
- 27. Трапеция Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на
- 28. Параллелограмм Противоположные стороны параллелограмма равны Противоположные углы параллелограмма равны Диагонали параллелограмма пересекаются, и точка пересечения делит
- 29. Прямоугольник и ромб d2 d1 Около любого прямоугольника можно описать окружность, причем диагональ прямоугольника равна диаметру
- 30. Правильные многоугольники
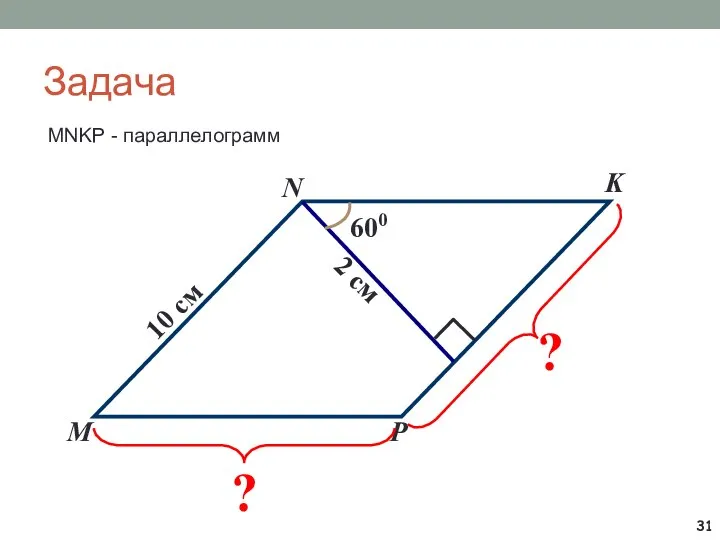
- 31. Задача MNKP - параллелограмм
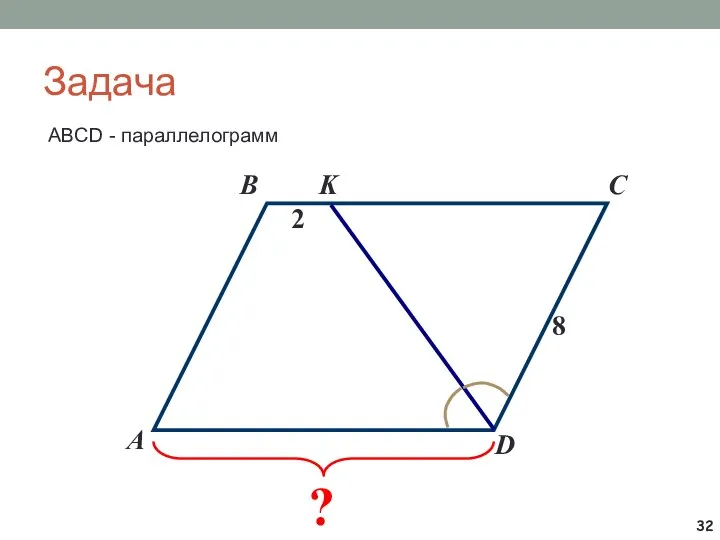
- 32. Задача ABCD - параллелограмм
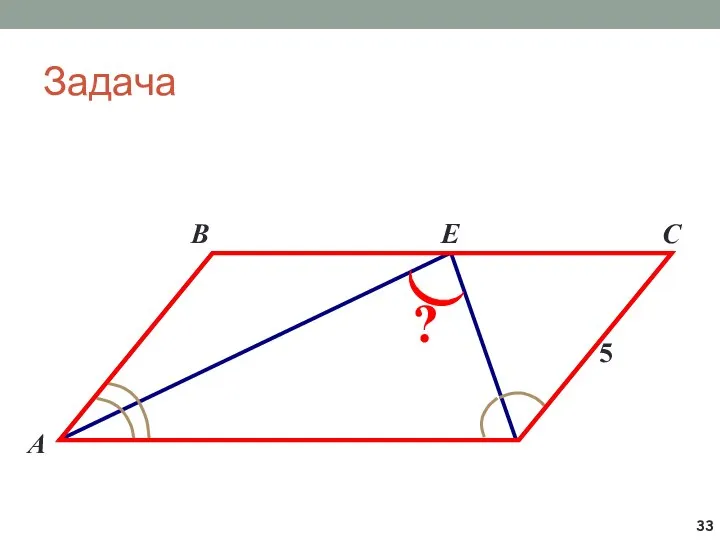
- 33. Задача
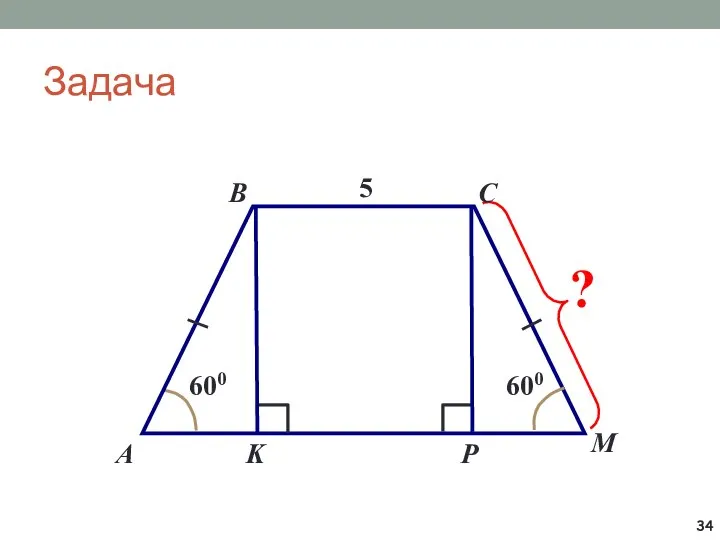
- 34. Задача
- 36. Скачать презентацию











 Неполные квадратные уравнения
Неполные квадратные уравнения Соотношение между сторонами и углами треугольника. Скалярное произведение векторов. (Вариант 1)
Соотношение между сторонами и углами треугольника. Скалярное произведение векторов. (Вариант 1) Измерение длины отрезка
Измерение длины отрезка Презентация на тему Пропорциональность величин (6 класс)
Презентация на тему Пропорциональность величин (6 класс)  Площадь сферы
Площадь сферы Преподаватель математики и информатики ГБОУ СПО РО «Константиновский педагогический колледж» Алексей Юлия Вадимовна
Преподаватель математики и информатики ГБОУ СПО РО «Константиновский педагогический колледж» Алексей Юлия Вадимовна Деление обыкновенных дробей
Деление обыкновенных дробей Площадь круга и площадь кругового сегмента
Площадь круга и площадь кругового сегмента Прямоугольный параллелепипед в задачах В8 ЕГЭ. Геометрия 11 класс
Прямоугольный параллелепипед в задачах В8 ЕГЭ. Геометрия 11 класс Экономический факторный анализ. Теорема о среднем
Экономический факторный анализ. Теорема о среднем L_2_Zakony_logiki_ravnosilnye_preobrazovania_lektsia
L_2_Zakony_logiki_ravnosilnye_preobrazovania_lektsia Алгебра. 7 класс
Алгебра. 7 класс Уравнение. Корень уравнения
Уравнение. Корень уравнения Посчитай кубики в постройке
Посчитай кубики в постройке Простейшие тригонометрические уравнения. Частные случаи. Уравнения, приводимые к алгебраическим
Простейшие тригонометрические уравнения. Частные случаи. Уравнения, приводимые к алгебраическим Презентация на тему Все действия с десятичными дробями (5 класс)
Презентация на тему Все действия с десятичными дробями (5 класс)  Дисперсионный анализ
Дисперсионный анализ Урок математики 17.09
Урок математики 17.09 Презентация на тему Длиннее короче
Презентация на тему Длиннее короче  Построение таблиц истинности для логических выражений
Построение таблиц истинности для логических выражений Дополнительные построения в трапеции при решении задач
Дополнительные построения в трапеции при решении задач Системы линейных уравнений
Системы линейных уравнений Урок математики в 4 классе
Урок математики в 4 классе Параллельность плоскостей
Параллельность плоскостей Διδακτική Ενότητα Α: Συνδυαστική Ανάλυση
Διδακτική Ενότητα Α: Συνδυαστική Ανάλυση Игра-тренажер. Веселая математика - геометрические фигуры
Игра-тренажер. Веселая математика - геометрические фигуры Отрезки (Начало)
Отрезки (Начало) Интегрирование неотрицательніх измериміх функций
Интегрирование неотрицательніх измериміх функций