Слайд 2Актуальность
Проблема
Непонимание математического смысла производной => неполноценность значения в различных областях наук.
Гипотеза

Использование дифференциальных уравнений лежит в основе физических законов.
Слайд 3План
Цели и задачи
Определение
История создания
Разбор темы
Применение в жизни
Задачи и вопросы

Слайд 4Цели и задачи
Цели:
Объяснить значение и смысл производных на конкретных примерах использования

в различных науках.
Задачи:
Изучить основы математического анализа.
Понять и научиться применять производную функций.
Найти и изучить примеры использования в разных науках.
Слайд 5Определение
Математический анализ –
совокупность разделов математики, соответствующих историческому разделу под наименованием «анализ бесконечно

малых», объединяет дифференциальное и интегральное исчисления.
Слайд 6История
Производная - одно из фундаментальных понятий математики. Оно возникло в XVII веке

в связи с необходимостью решения ряда задач из физики, механики и математики, но в первую очередь следующих двух: определение скорости прямолинейного движения и построения касательной к прямой.
В частности, используя методы дифференциального исчисления, ученые предсказали возвращение кометы Галлея, что было большим триумфом науки XVIII в. С помощью тех же методов математики изучали в XVII и XVIII вв. различные кривые.
Слайд 8Понятие о производной
Производная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции

(в данной точке).
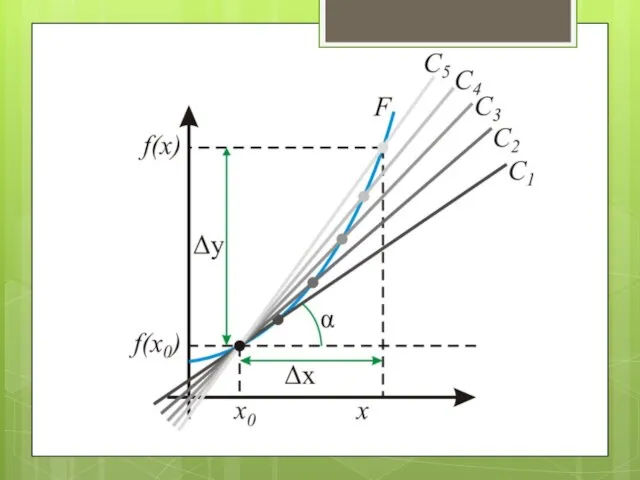
Производной функции f в точке x0 называется число, к которому стремится разностное отношение
при Δx, стремящемся к нулю
Процесс вычисления производной называется дифференцированием. Обратный процесс — нахождение первообразной — интегрирование.
Слайд 9Определение производной
Пример1
Найти производную функции f(x)=x3 в точке x0 .
1) Δf = (x0+

Δx)3-x03 = 3x02Δx + 3x0(Δx)2 +(Δx)3
2) Δf/ Δx = 3x02 + 3x0Δx + (Δx)2 ;(Δx ≠0).
3) 3x02 постояно, а при Δx →0 ,
3x0 Δx →0 и (Δx)2 →0 => 3x0 Δx + (Δx)2 →0 ;
Δf/ Δx → 3x02 при Δx →0 => f’(x0)= 3x02
Слайд 11предел
Преде́л фу́нкции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина,
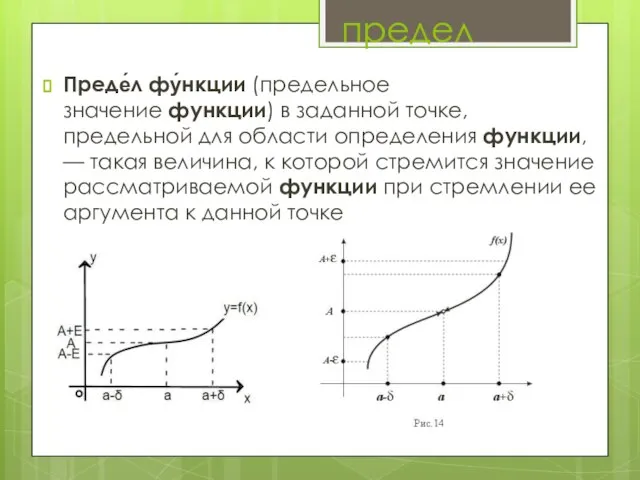
к которой стремится значение рассматриваемой функции при стремлении ее аргумента к данной точке
Слайд 13Примеры и задачи по теме предел функции

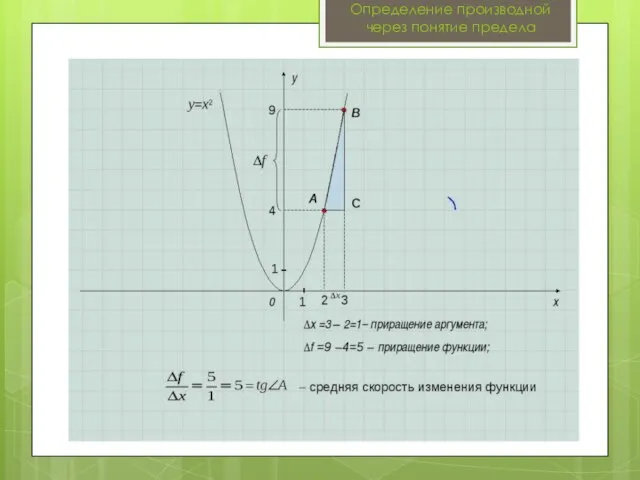
Слайд 14Определение производной через понятие предела
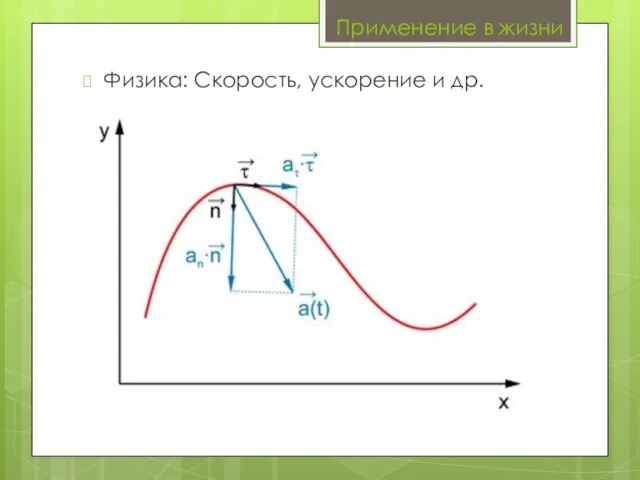
Слайд 15Применение в жизни
Физика: Скорость, ускорение и др.
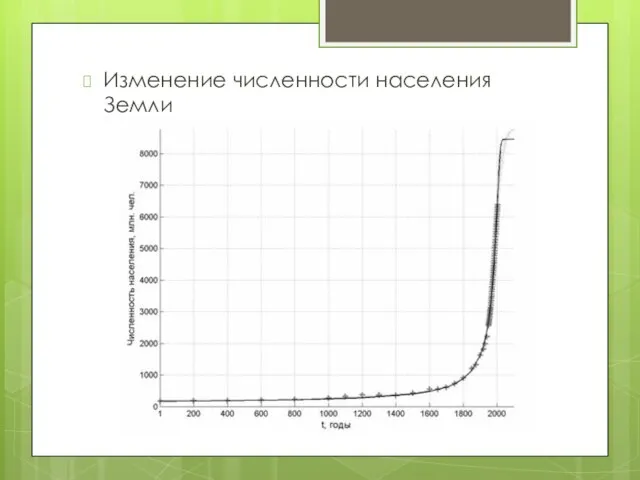
Слайд 16Изменение численности населения Земли















 Графический диктант. Тема: Делимость чисел
Графический диктант. Тема: Делимость чисел Нахождение числа по его дроби. Урок-игра Детективное агентство
Нахождение числа по его дроби. Урок-игра Детективное агентство Решение линейных неравенств
Решение линейных неравенств Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций. Урок 45
Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций. Урок 45 Уравнение прямой на координатной плоскости
Уравнение прямой на координатной плоскости Презентация на тему Измерение высоты предмета
Презентация на тему Измерение высоты предмета  Интеграл. Формула Ньютона-Лейбница
Интеграл. Формула Ньютона-Лейбница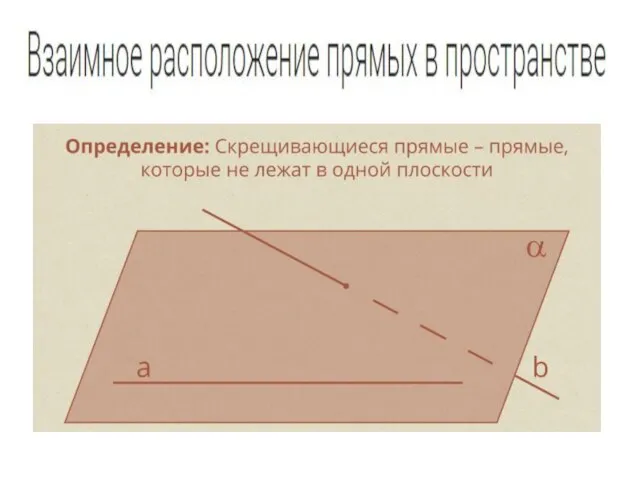 Взаимное расположение прямых в пространстве
Взаимное расположение прямых в пространстве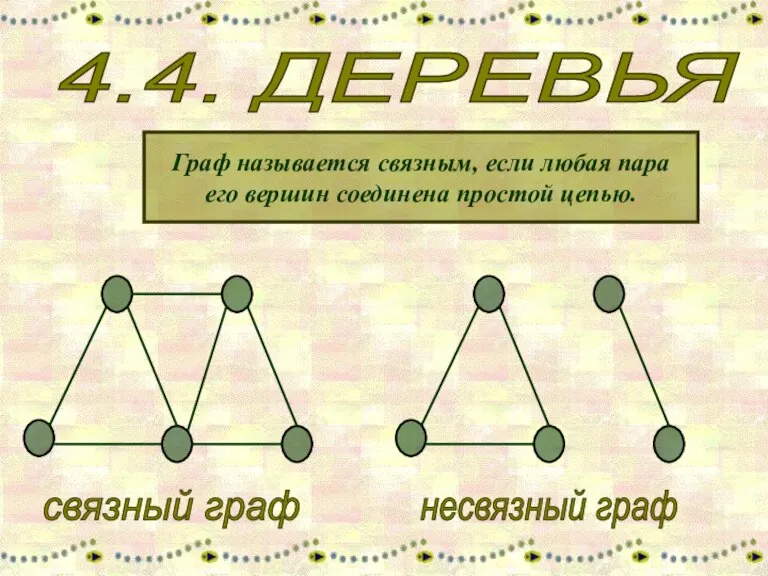 Деревья
Деревья Пересечение высот
Пересечение высот Проценты (5)
Проценты (5) Виды графов. Тема 4.2
Виды графов. Тема 4.2 Как построена задача, какие части есть в задаче
Как построена задача, какие части есть в задаче Теория вероятностей и математическая статистика. Двумерные случайные величины. Лекция 8
Теория вероятностей и математическая статистика. Двумерные случайные величины. Лекция 8 Представьте в виде неправильной дроби
Представьте в виде неправильной дроби Вычисление производных с помощью правил дифференцирования
Вычисление производных с помощью правил дифференцирования Теорема Пифагора
Теорема Пифагора Проецирование правильной шестиугольной призмы
Проецирование правильной шестиугольной призмы Случайный выбор точки из отрезка
Случайный выбор точки из отрезка Задачи на площадь
Задачи на площадь Статистическая проверка статистических гипотез
Статистическая проверка статистических гипотез Точка. Кривая линия. Прямая линия. Отрезок
Точка. Кривая линия. Прямая линия. Отрезок Позиция 7 ЕГЭ 2016. Физический смысл производной
Позиция 7 ЕГЭ 2016. Физический смысл производной Модуль. Определение. Свойства. Геометрический смысл модуля
Модуль. Определение. Свойства. Геометрический смысл модуля Моменты случайной величины
Моменты случайной величины mypresentation.ru
mypresentation.ru Задачи на умножение. 2 класс
Задачи на умножение. 2 класс Уровень и отвес
Уровень и отвес