Основные понятия комбинаторики

Комбинаторика
– это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.
десятки - от 1 до9, т.е. 9
единицы - от 0 до 9, т.е. 10
Количество вариантов 9.10=90

Правило произведения
Если существует m вариантов выбора первого элемента и для каждого из них имеется n вариантов выбора второго элемента, то всего существует m • n различных пар с выбранными таким образом первым и вторым элементами.

Задача 1
Сколько различных двузначных чисел можно записать с помощью цифр 0, 1, 2, 3?
Решение:
m = 3, n = 4; m • n = 12
Ответ: 12
Задача 2
Сколько различных трехзначных чисел можно записать с помощью цифр 0, 1, 2, 3?
Решение:
m=3, n=4, k=4; mnk=3 • 4 • 4 =48
Ответ: 48
Задача 3
Сколько различных пятибуквенных слов можно записать с помощью букв «и» и «л»?
Решение:
a = 2, b = 2, c = 2, d = 2, f=2;
Ответ: 32
= 32
2 • 2 • 2 • 2 • 2 =
abcdf =

Упражнения:
№ 1
Сколько различных двузначных чисел с разными цифрами можно записать, используя цифры:
1вариант: 1) 1, 2 и 3; 3) 5, 6, 7 и 8; 5) 0, 2, 4 и 6;
2 вариант: 2) 4, 5, и 6; 4) 6, 7, 8 и 9; 6) 0, 3, 5 и 7?
Ответ: 1), 2) 6; 3), 4) 12; 5), 6) 9.
№ 2
Сколько различных трехзначных чисел можно записать с помощью цифр:
1 вариант: 1) 2 и 3; 3) 0 и 2;
2 вариант: 2) 8 и 9; 4) 0 и 5?
Ответ: 1), 2) 8; 3),4) 4.

№ 3
Сколько различных трехзначных чисел, не имеющих одинаковых цифр, можно записать с помощью цифр:
1 вариант: 1) 3, 4 и 5; 3) 5, 6, 7 и 8;
2 вариант: 2) 7, 8, и 9; 4) 1, 2, 3 и 4?
Ответ: 1),2) 6; 3),4) 24.
№ 4
Сколько различных четырехбуквенных «слов» можно записать с помощью букв:
1 вариант: 1) «м» и «а»; 3) «к», «а» и «о»;
2 вариант: 2) «п» и «а»; 4) «ш», «а» и «л».
Ответ: 1), 2) 16; 3), 4) 81.
С.Р.

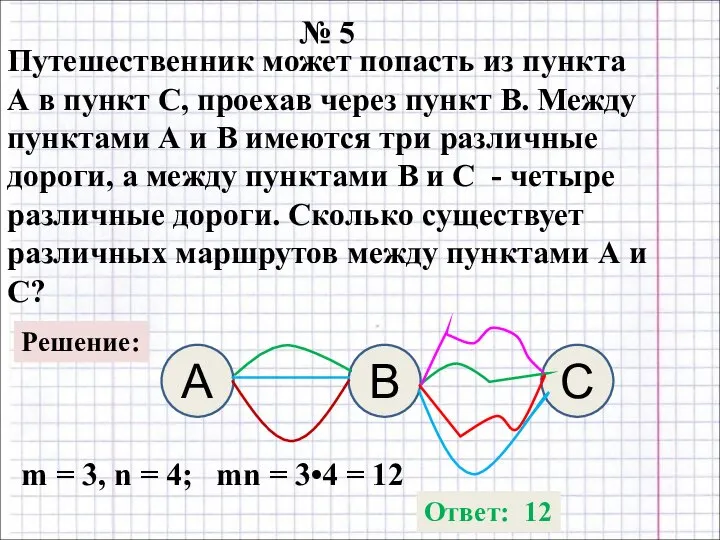
№ 5
Путешественник может попасть из пункта А в пункт С, проехав через пункт В. Между пунктами А и В имеются три различные дороги, а между пунктами В и С - четыре различные дороги. Сколько существует различных маршрутов между пунктами А и С?
Решение:
m = 3, n = 4; mn = 3•4 = 12
Ответ: 12

№ 6
Чтобы попасть из города М в город К, нужно проехать через город N. Между городами М и N имеются четыре автодороги, а из города N в город К можно попасть либо поездом, либо самолетом. Сколько существует различных способов добраться из города М в город К?
Ответ: 8
С.Р.

7.
8.
9.
1) 992 2) 240
120
1) 720 2) 120
Сколькими способами могут распределиться золотая и серебряная медали на чемпионате по футболу, если в нем принимают участие:
1) 32 команды; 2) 16 команд?
Сколькими способами можно составить расписание 5 уроков на один день из 5 различных предметов?
Сколькими способами могут занять очередь в школьный буфет:
1) 6 учащихся; 2) 5 учащихся?

11.
12.
13.
В классе 18 учащихся. Из их числа нужно выбрать физорга, культорга и казначея. Сколькими способами это можно сделать, если один ученик может занимать не более одной должности?
В классе 20 учащихся. Необходимо назначить по одному дежурному в столовую, вестибюль и спортивный зал. Сколькими способами это можно сделать?
Сколько существует пятизначных чисел, в которых все цифры, стоящие на нечетных местах, различны?
4896
6840
64800