Содержание
- 2. ЦЕЛИ: Рассмотрев использование комбинаторики в различных сферах жизнедеятельности, повторить формулы для вычисления числа перестановок, размещений и
- 3. Комбинаторика – самостоятельная ветвь математической науки - это раздел математики, в котором изучаются простейшие «соединения»: перестановки,
- 4. «Вперед поедешь – голову сложишь, направо поедешь – коня потеряешь, налево поедешь – меча лишишься.
- 5. Перестановки – соединения, которые можно составить из n предметов, меняя всеми возможными способами их порядок; число
- 6. n-факториал- это произведение всех натуральных чисел от до единицы до n, обозначают символом ! Используя знак
- 7. Задача Квартет Проказница Мартышка Осёл, Козёл, Да косолапый Мишка Затеяли играть квартет … Стой, братцы стой!
- 8. Решение: Здесь n=4, поэтому способов «усесться чинно в ряд» имеется P = 4! = 1 *
- 9. Размещения – соединения, содержащие по m предметов из числа n данных, различающихся либо порядком предметов, либо
- 10. Задача В группе ТД – 21 обучается 24 студента. Сколькими способами можно составить график дежурства по
- 11. Решение задачи: Ответ: число способов равно числу размещений из 24 по 3, т.е. 12144 способа.
- 12. Сочетания– соединения, содержащие по m предметов из n, различающихся друг от друга, по крайней мере, одним
- 13. Задача Студентам дали список из 10 учебников, которые рекомендуется использовать для подготовки к экзамену . Сколькими
- 14. Решение задачи: Ответ: число способов равно числу сочетаний из 10 по 3, т.е. 120 способов.
- 15. Библиографическая справка Термины «перестановки» и «размещения» впервые употребил Якоб Бернулли в книге «Искусство предположений». Термин «сочетания»впервые
- 16. Особая примета комбинаторных задач - вопрос, который начинался словами «Сколькими способами…?»
- 17. Решение задач: Задача №1: В соревнованиях участвуют 12 команд. Сколько существует вариантов распределения призовых (I, II,
- 18. Исторические сведения Комбинаторика как наука стала развиваться в XIII в. параллельно с возникновением теории вероятностей. Первые
- 19. Исторические сведения Дата рождения: 1 июля 1646 г. Место рождения: Лейпциг, Германия Дата смерти:14 ноября 1716
- 20. Связь комбинаторики с другими областями математики: Имеет широкий спектр применения в информатике и статистической физике алгебра,
- 21. Фигурные числа . Солдаты стоят правильными рядами, образуя квадраты. Число солдат внутри такого квадрата легко подсчитать
- 22. Фигурные числа В древности вычислители часто считали с помощью камешков и, естественно, отмечали случаи, когда камешки
- 23. Комбинаторика в различных областях жизнедеятельности человека. Литература Былины Сказки_ Басни__
- 24. Электротехника В коридоре висят три лампочки. Сколько имеется различных способов освещения коридора?
- 25. Государственная символика
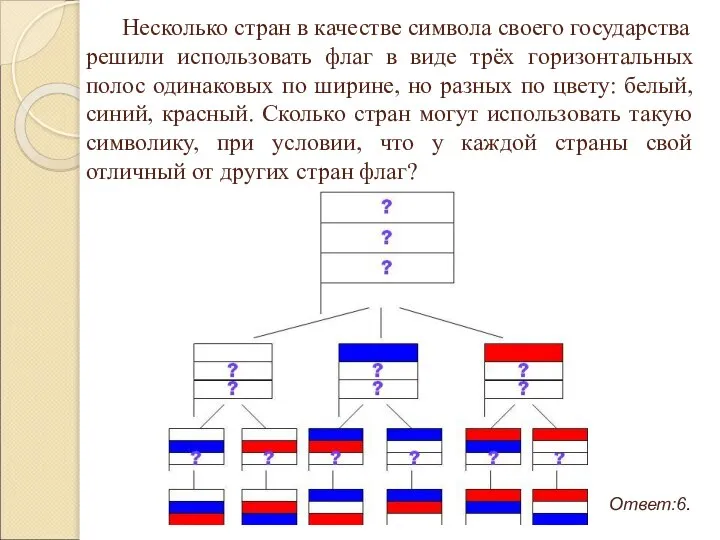
- 26. Несколько стран в качестве символа своего государства решили использовать флаг в виде трёх горизонтальных полос одинаковых
- 27. Игра Шахматы Выдающиеся шахматисты Клод Шеннон и Михаил Ботвинник внесли огромный вклад в создание математической модели
- 28. Игра Кубик Рубика Необыкновенно популярной головоломкой стал кубик Рубика, изобретенный в 1975 году преподавателем архитектуры из
- 29. Меню на завтрак На завтрак Вова может выбрать: плюшку, бутерброд, пряник, или кекс, а запить он
- 31. Скачать презентацию



























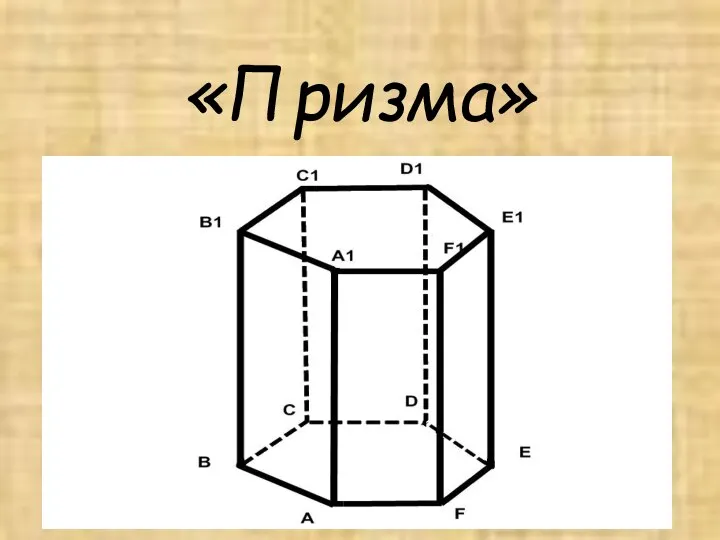 Призма. Определение призмы
Призма. Определение призмы Интеллектуальная игра Самый умный. Информатика. Математика
Интеллектуальная игра Самый умный. Информатика. Математика Длина окружности
Длина окружности Планиметрия: задачи, связанные с углами. Применение тригонометрии в геометрических задачах
Планиметрия: задачи, связанные с углами. Применение тригонометрии в геометрических задачах Построение треугольника по трем элементам
Построение треугольника по трем элементам Математический счет. Весёлые задачки
Математический счет. Весёлые задачки Матричный способ решения СЛАУ и метод Крамера
Матричный способ решения СЛАУ и метод Крамера Повторение курса геометрии. 7 класс
Повторение курса геометрии. 7 класс Таблица единиц площади
Таблица единиц площади Probability Distributions
Probability Distributions Метрологическое обеспечение на базе профессионального стандарта Специалист по метрологии
Метрологическое обеспечение на базе профессионального стандарта Специалист по метрологии Многогранники. Розв'язування задач
Многогранники. Розв'язування задач Презентация на тему Осевая и центральная симметрия (8 класс)
Презентация на тему Осевая и центральная симметрия (8 класс)  Гласные звуки и буквы. Слова с буквой Э
Гласные звуки и буквы. Слова с буквой Э Деление с остатком
Деление с остатком Презентация на тему Функция у=х^2, её свойства и график
Презентация на тему Функция у=х^2, её свойства и график  Дорогу осилит идущий, геометрию – думающий. Площадь параллелограмма
Дорогу осилит идущий, геометрию – думающий. Площадь параллелограмма Понятие десятичной дроби
Понятие десятичной дроби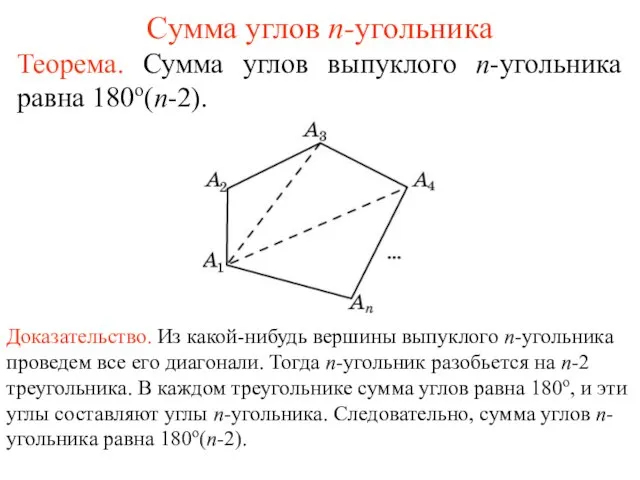 Презентация на тему Сумма углов n-угольника
Презентация на тему Сумма углов n-угольника  Умножение и деление смешанных дробей
Умножение и деление смешанных дробей Множества и отношения
Множества и отношения Производная сложной функции
Производная сложной функции Пирамида. Высрта пирамиды
Пирамида. Высрта пирамиды Сравнение дробей
Сравнение дробей Дискретные случайные величины
Дискретные случайные величины Геометрическая и арифметическая прогрессии. Повторительно-обобщающий урок
Геометрическая и арифметическая прогрессии. Повторительно-обобщающий урок Алгоритмическая конструкция Ветвление
Алгоритмическая конструкция Ветвление Презентация по математике "Правило умножения для комбинаторных задач" -
Презентация по математике "Правило умножения для комбинаторных задач" -