Слайд 2Преобразования, связанные с системой координат
Для управления изображением на экране, нужно вносить изменения

в его положение, форму, ориентацию, размер. Для этих целей существуют специальные геометрические преобразования, которые позволяют изменять эти характеристики объектов в пространстве.
Существуют три основных преобразований:
Перемещение (перенос)
Масштабирование
Вращение
Слайд 3Перемещение
Перенос перемещает объект в другую позицию на экране не меняя при этом

размеры и форму объекта.
Можно перевести точку в 2D, добавив координату перемещения (t x , t y ) к исходной координате (X, Y), чтобы получить новую координату (X ‘, Y’).
Слайд 4продолжение
X ‘= X + t x
Y ‘= Y + t y
Пара (t x , t y ) называется

вектором перевода или вектором сдвига. Приведенные выше уравнения также могут быть представлены с использованием векторов столбцов.
Математически этот перенос можно описать с помощью вектора переноса . Пусть радиус вектор, соответствующий вектору переноса . Тогда переход из точки в точку будет соответствовать векторной записи . Отсюда получаем, что для переноса точки в новое положение необходимо добавить к ее координатам некоторые числа, которые представляют собой координаты вектора переноса:
Слайд 5Масштабирование
Масштабированием объектов называется растяжение объектов вдоль соответствующих осей координат относительно начала координат

или относительно точки сцены.
Эта операция применяется к каждой точке объекта, поэтому можно также говорить о масштабировании точки. При этом, конечно, речь не идет об изменении размеров самой точки.
Масштабирование достигается умножением координат точек на некоторые константы по осям называемые коэффициентами масштабирования.
Слайд 6продолжение
Когда коэффициенты масштабирования равны между собой, масштабирование называется однородным.
После применения операции однородного
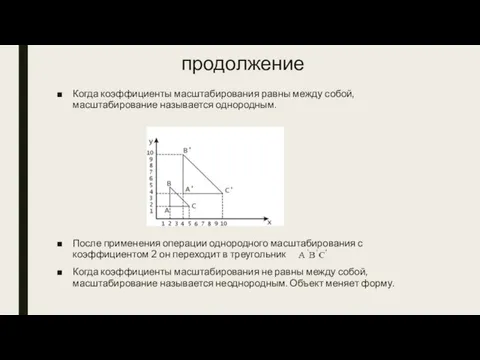
масштабирования с коэффициентом 2 он переходит в треугольник
Когда коэффициенты масштабирования не равны между собой, масштабирование называется неоднородным. Объект меняет форму.
Слайд 7продолжение
X ‘= X * S x
Y ‘= Y * S y
Матрица масштабирования

будет:
Для точки операция масштабирования в матричном виде будет выглядеть следующим образом:
Слайд 8Вращение
Вращение это поворот объект на определенный угол θ (тета) относительно начала координат

или относительно точки сцены.
Точка P (X, Y) расположена под углом φ от горизонтальной координаты X с расстоянием r от начала координат.
Если повернуть его на угол θ, получаем новую точку P ‘(X’, Y ‘).
Слайд 9продолжение
Найдем преобразование координат точки Р в точку P’ при вращении.

Слайд 10Дополнительные преобразования
отражение
Отражение — это зеркальное отражение оригинального объекта. Это операция поворота на 180

°. При преобразовании отражения размер объекта не изменяется.
На следующих рисунках показаны отражения относительно осей X и Y и начала координат соответственно.
Слайд 11ножницы
Преобразование, которое наклоняет форму объекта, называется сдвиговым преобразованием.
Существуют две трансформации сдвига

X-Shear и Y-Shear . Один сдвигает значения координат X, а другой сдвигает значения координат Y.
Тем не мение в обоих случаях только одна координата меняет свои координаты, а другая сохраняет свои значения. Стрижка также называется Skewing.
Слайд 12продолжение
X-Shear
X-Shear сохраняет координату Y, и в координаты X вносятся изменения, в результате

чего вертикальные линии наклоняются вправо или влево, как показано на рисунке ниже.











 Задача на арифметическую прогрессию (1)
Задача на арифметическую прогрессию (1)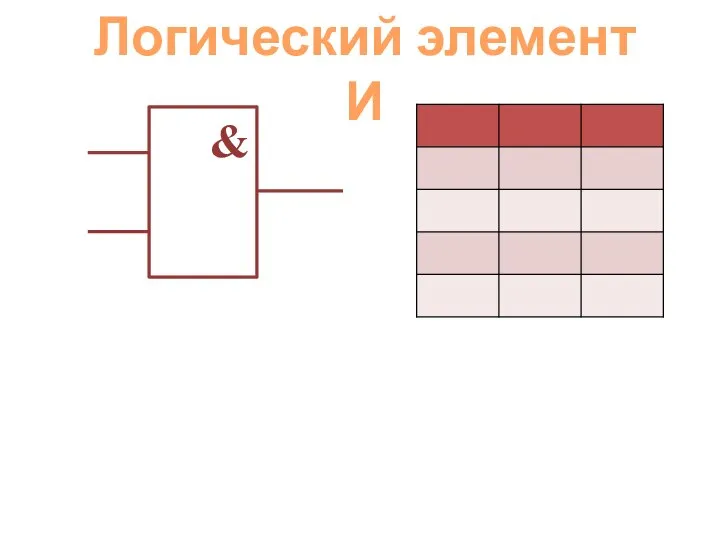 Логический элемент
Логический элемент Тригонометрические уравнения
Тригонометрические уравнения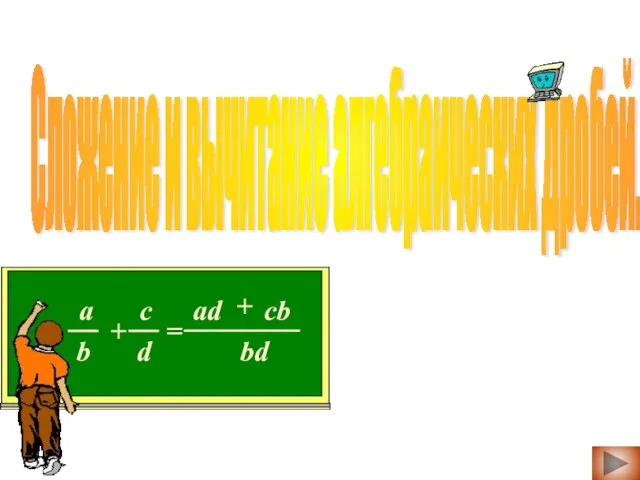 Сложение и вычитание алгебраических дробей
Сложение и вычитание алгебраических дробей Основные задачи и область применения дискретной математики
Основные задачи и область применения дискретной математики Симетричні фігури
Симетричні фігури Лекция 5. Плоские и планарные графы
Лекция 5. Плоские и планарные графы Презентация на тему Объем прямой призмы
Презентация на тему Объем прямой призмы  Стереометрия. 1
Стереометрия. 1 Сравнение чисел
Сравнение чисел Физический и механический смысл производных. Использование производной в физике, механике
Физический и механический смысл производных. Использование производной в физике, механике Решение задач
Решение задач Презентация на тему Является ли система координат чисто математическим понятием
Презентация на тему Является ли система координат чисто математическим понятием  Аналоги теореми порівняння Колмогорова та їх застосування
Аналоги теореми порівняння Колмогорова та їх застосування Больше, меньше, столько же
Больше, меньше, столько же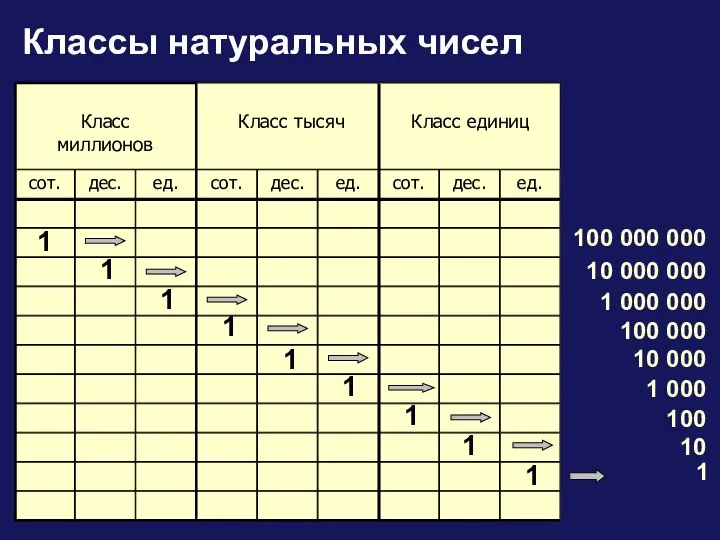 Классы натуральных чисел
Классы натуральных чисел Исследование функции на монотонность
Исследование функции на монотонность Построить линейный угол двугранного угла
Построить линейный угол двугранного угла Элементы комбинаторики
Элементы комбинаторики Сложение с переходом через десяток
Сложение с переходом через десяток Сумма n первых членов геометрической прогрессии (9 класс)
Сумма n первых членов геометрической прогрессии (9 класс) Действия с десятичными дробями
Действия с десятичными дробями Показательные уравнения и неравенства
Показательные уравнения и неравенства Тригонометрические уравнения Однородные тригонометрические уравнения
Тригонометрические уравнения Однородные тригонометрические уравнения Использование свойств действий при вычислениях. Наглядный материал к уроку
Использование свойств действий при вычислениях. Наглядный материал к уроку Математический хоккей
Математический хоккей Арифметический корень натуральной степени
Арифметический корень натуральной степени Введение в математическую логику и теорию множеств
Введение в математическую логику и теорию множеств