Содержание
- 2. Описательная статистика Медиана (2 часа) Бахова А.Б. МОУ СОШ №6
- 3. Не только среднее арифметическое показывает, где на числовой прямой располагаются числа какого-либо набора и где их
- 4. Пример 1 Возьмем какой-нибудь набор различных чисел, например 1, 4, 7, 9, 11. Подберем число m
- 5. Пример 2 Рассмотрим набор 1, 3, 6, 11. Найти медиану набора. Числа тоже записаны по возрастанию,
- 6. Пример 3(а) Найти медиану набора 12, 2, 11,3, 7, 10, 3. Расположим числа по возрастанию: 2,
- 7. Пример 3 (б) Найти медиану набора 12, 2, 11, 3, 7, 10, 3, 15. Расположим числа
- 8. Пример 3 (в) Найти медиану набора 1, 2, 2, 2, 3, 3. Расположим числа по возрастанию:
- 9. Определение 1. Медианой набора различных чисел называют такое число (скажем m), которое обладает следующим свойством: количество
- 10. Пример 4 Производство пшеницы в России в 1995-2001 гг. млн.тонн Средний урожай равен Найдем медиану: 27,0;
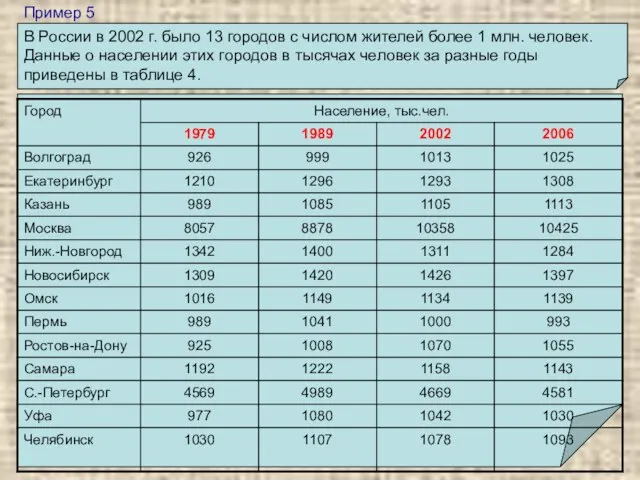
- 11. Пример 5 В России в 2002 г. было 13 городов с числом жителей более 1 млн.
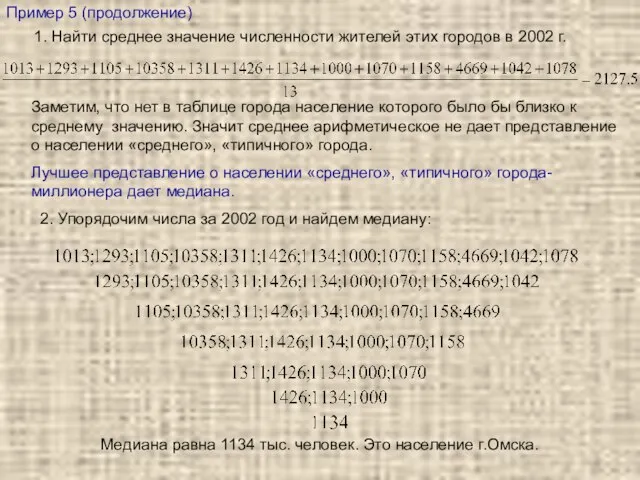
- 12. Пример 5 (продолжение) 1. Найти среднее значение численности жителей этих городов в 2002 г. Заметим, что
- 13. Упражнения №1 Вычислите медиану и среднее арифметическое чисел, сравните медиану и среднее значение: 1, 3, 5,
- 14. №3 Отметьте числа и их медианы на числовой оси: 8, 11, 3; 7, 4, 8, 1,
- 15. №6 Найдите медиану следующих наборов чисел: 2, 4, 8, 9; 1, 3, 5, 7, 8, 9;
- 16. №8 Рассмотрите данные о числе жителей крупнейших городов России (таблица 4), исключив из них Москву и
- 18. Скачать презентацию













 Определители второго и третьего порядка
Определители второго и третьего порядка Длина
Длина Логические задачи. Задачи со спичками
Логические задачи. Задачи со спичками Многогранники. Понятие многогранника. Призма
Многогранники. Понятие многогранника. Призма Множества
Множества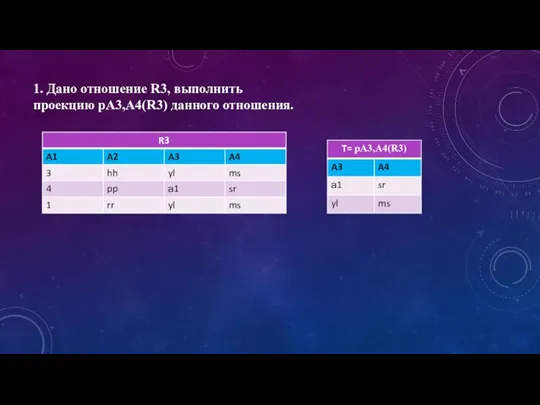 Дано отношение R3, выполнить проекцию pA3,A4(R3) данного отношения
Дано отношение R3, выполнить проекцию pA3,A4(R3) данного отношения Методы и приемы решения дробно-рациональных уравнений, содержащих параметр
Методы и приемы решения дробно-рациональных уравнений, содержащих параметр Переход от передаточных функций к дифференциальным уравнениям и структурным схемам
Переход от передаточных функций к дифференциальным уравнениям и структурным схемам Площадь круга. Геометрическая сказка. 6 класс
Площадь круга. Геометрическая сказка. 6 класс Тригонометрические функции. Формулы двойного угла
Тригонометрические функции. Формулы двойного угла Решение задач. Пирамида
Решение задач. Пирамида Прямоугольный параллелепипед. Многогранники
Прямоугольный параллелепипед. Многогранники Аксиомы стереометрии
Аксиомы стереометрии Случаи сложения вида +6
Случаи сложения вида +6 Десятичные дроби
Десятичные дроби Задачи на соответствие графиков формулам их задающим
Задачи на соответствие графиков формулам их задающим Иррациональные уравнения
Иррациональные уравнения Золотое сечение
Золотое сечение Пирамида, её основание, вершина, боковые рёбра, высота, боковая поверхность
Пирамида, её основание, вершина, боковые рёбра, высота, боковая поверхность Роль дистанционных конкурсов по математике в гуманитарном развитии обучающихся
Роль дистанционных конкурсов по математике в гуманитарном развитии обучающихся Решение задач. Подготовка к умножению
Решение задач. Подготовка к умножению Сравнение предметов по некоторой величине без её измерения: выше - ниже, шире - уже
Сравнение предметов по некоторой величине без её измерения: выше - ниже, шире - уже Морское путешествие
Морское путешествие Устный счёт Прицепи вагоны. 2 класс
Устный счёт Прицепи вагоны. 2 класс Обратные задакчи
Обратные задакчи Отношения и пропорции. Повторение
Отношения и пропорции. Повторение Однородные тригонометрические уравнения
Однородные тригонометрические уравнения Úsh perpendıkýlıar týraly teorema
Úsh perpendıkýlıar týraly teorema