Содержание
- 2. Тема урока Элементы комбинаторики. Перестановки.
- 3. Таблица факториалов: Определение. Открываем новое Факториал Факториалом натурального числа n называется произведение всех натуральных чисел от
- 4. На примерах учимся №748 Найдите значение выражения
- 5. На примерах учимся №746
- 6. Определение. Число всевозможных перестановок из n элементов вычисляется по формуле: Pn = n! Открываем новое Перестановки
- 7. Сколькими способами могут быть расставлены восемь участниц финального забега на восьми беговых дорожках? Решение: P8 =
- 8. Сколько различных четырёхзначных чисел можно составить из цифр 0, 1, 2, 3, причём в каждом числе
- 9. Имеется 10 различных книг, среди которых есть трёхтомник одного автора. Сколькими способами можно расставить эти книги
- 10. На примерах учимся №1 Сколькими способами могут встать в очередь в билетную кассу: 1) 3 человека;
- 11. На примерах учимся №2 Сколько различных правильных (с точки зрения русского языка) фраз можно составить, изменяя
- 12. На примерах учимся №3 Сколькими способами можно с помощью букв К, L, М, Н обозначить вершины
- 13. На примерах учимся №735 Сколько существует выражений, тождественно равных произведению abcde, которые получаются из него перестановкой
- 14. На примерах учимся №736 Ответ: 6 вариантов. Ольга помнит, что телефон подруги оканчивается цифрами 5, 7,
- 15. (Олег находится в конце ряда). Число комбинаций равно числу перестановок 6 мальчиков, стоящих перед Олегом: На
- 16. (Олег находится в конце ряда). Число комбинаций равно числу перестановок 6 мальчиков, стоящих перед Олегом: На
- 17. На примерах учимся №737 Ответ: 720 чисел; 600 чисел. Сколько шестизначных чисел (без повторения цифр) можно
- 18. Что изучает комбинаторика? Кем был введен в математический обиход термин «комбинаторика»? Какие способы решения комбинаторных задач
- 20. Скачать презентацию

















 Играем с Капитошкой. Игра-тренажёр по теме Таблица сложения
Играем с Капитошкой. Игра-тренажёр по теме Таблица сложения Виды треугольников. 5 класс
Виды треугольников. 5 класс Старинные меры длины на Руси
Старинные меры длины на Руси Первообразная функции
Первообразная функции Формулы. Повторение
Формулы. Повторение Развернутый план-конспект открытого урока по математике ГОУ НПО ПЛ №35 Саратов,2011
Развернутый план-конспект открытого урока по математике ГОУ НПО ПЛ №35 Саратов,2011 Системы счисления
Системы счисления Понятие обыкновенной дроби. Упражнения
Понятие обыкновенной дроби. Упражнения В мире геометрии
В мире геометрии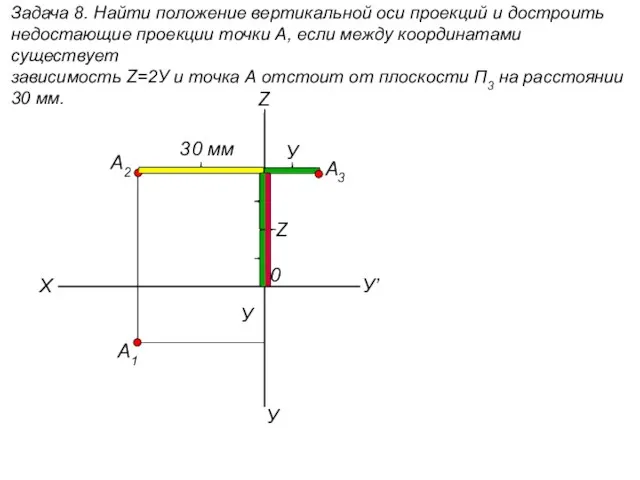 Найти положение вертикальной оси проекций и достроить недостающие проекции точки А. (задача 8)
Найти положение вертикальной оси проекций и достроить недостающие проекции точки А. (задача 8) Комбинаторика и теория вероятности
Комбинаторика и теория вероятности Односторонние пределы
Односторонние пределы Цилиндр в математике
Цилиндр в математике Презентация на тему Смежные углы
Презентация на тему Смежные углы  Геометрические тела и фигуры
Геометрические тела и фигуры Математическая игра Петергофская мозаика 5 класс
Математическая игра Петергофская мозаика 5 класс Реляционная алгебра
Реляционная алгебра Задачи с цифрами 1, 5, 9
Задачи с цифрами 1, 5, 9 Комбинаторные методы решения вероятностных задач
Комбинаторные методы решения вероятностных задач Сборник задач Во имя тех священных дней
Сборник задач Во имя тех священных дней Наименьшее и наибольшее значение функции. Задачи
Наименьшее и наибольшее значение функции. Задачи Равносильность уравнений. Линейные уравнения
Равносильность уравнений. Линейные уравнения Контрольна робота 1 (геометрія)
Контрольна робота 1 (геометрія) Метрология
Метрология Регулятивные удд
Регулятивные удд Кто что любит поесть?
Кто что любит поесть? Интеграл. Формула Ньютона-Лейбница. Что называют криволинейной трапецией?
Интеграл. Формула Ньютона-Лейбница. Что называют криволинейной трапецией? Поверхности и тела. Проецирование геометрических фигур
Поверхности и тела. Проецирование геометрических фигур