знакомы с глубокой древности. В 1906 г. была обнаружена книга Архимеда (287 – 212 гг. до н.э.) «О методе», в которой дается решение задачи об объеме общей части пересекающихся цилиндров. Архимед приписывает честь открытия этого принципа Демокриту (470 – 380 гг. до н.э.) – древнегреческому философу-материалисту. С помощью этого принципа Демокрит получил формулы для вычисления объема пирамиды и конуса.
Много сделала для геометрии школа Платона (428 – 348 гг. до н.э.). Платон был учеником Сократа (470 – 399 гг. до н.э.). Он в 387 г. до н.э. основал в Афинах Академию, в которой работал 20 лет. Каждый, входящий в Академию, читал надпись: «Пусть сюда не входит никто, не знающий геометрии». Школе Платона, в частности, принадлежит:
а) исследование свойств призмы, пирамиды, цилиндра, конуса;
б) изучение конических сечений.
Большой трактат о конических сечениях был написан Аполлонием Пергским (260 – 170 гг. до н.э.) – учеником Евклида (III в. до н.э), который создал великий труд из 15 книг под названием «Начала». Эти книги издаются и по сей день, а в школах Англии по ним учатся до сих пор.
НЕМНОГО ИСТОРИИ













 Презентация на тему НАХОЖДЕНИЕ НАИБОЛЬШЕГО И НАИМЕНЬШЕГО ЗНАЧЕНИЯ ФУНКЦИИ
Презентация на тему НАХОЖДЕНИЕ НАИБОЛЬШЕГО И НАИМЕНЬШЕГО ЗНАЧЕНИЯ ФУНКЦИИ  Алгебра в жизни человека
Алгебра в жизни человека Многогранники в нашей жизни
Многогранники в нашей жизни Построение призмы с вырезом
Построение призмы с вырезом Первая теорема сравнения
Первая теорема сравнения Тождественные преобразования алгебраических выражений (часть 1)
Тождественные преобразования алгебраических выражений (часть 1) Числовая окружность
Числовая окружность Исследование функций с помощью производных. Правила Лопиталя
Исследование функций с помощью производных. Правила Лопиталя Пределы. Раскрытие неопределенности. 2 часть
Пределы. Раскрытие неопределенности. 2 часть Определители. Матрица и ее определитель
Определители. Матрица и ее определитель Логарифмы вокруг нас
Логарифмы вокруг нас В мире геометрии
В мире геометрии Штангенциркуль. Проведение измерений с помощью штангенциркуля
Штангенциркуль. Проведение измерений с помощью штангенциркуля Векторы
Векторы Нуль без палочки. Математический турнир
Нуль без палочки. Математический турнир Вычитание вида 8 - ,9-
Вычитание вида 8 - ,9-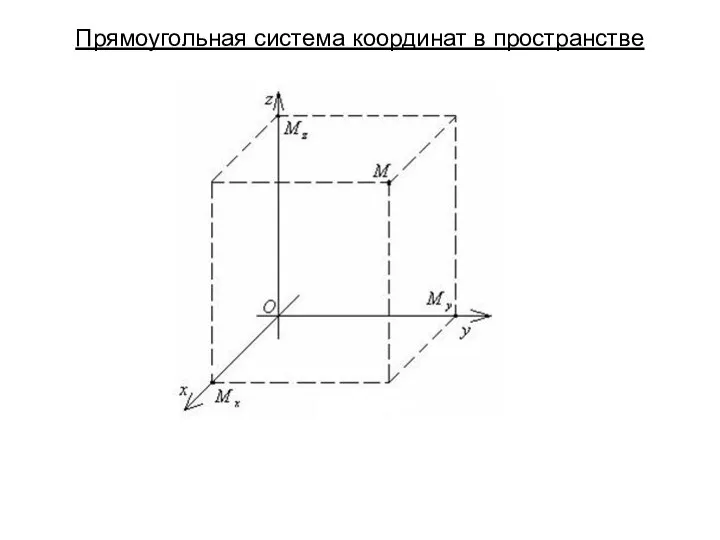 Прямоугольная система координат в пространстве. Понятие вектора
Прямоугольная система координат в пространстве. Понятие вектора Скрипт параллелограм
Скрипт параллелограм Двойные интегралы
Двойные интегралы Геометрия на каждом уроке
Геометрия на каждом уроке Преобразование графиков функции
Преобразование графиков функции Вычисление неопределенного интеграла
Вычисление неопределенного интеграла Сумма углов треугольника
Сумма углов треугольника Повторение. Урок для 8 класса
Повторение. Урок для 8 класса Виды углов
Виды углов Классическое определение вероятности события
Классическое определение вероятности события Подготовка к ЕГЭ В8
Подготовка к ЕГЭ В8 Применение производной к исследованию функций
Применение производной к исследованию функций