Содержание
- 2. Титульный лист Содержание История появления тригонометрии Знаки Sin, Cos, Tg, Ctg Формулы приведения Формулы суммы и
- 3. История тригонометрии, как наука о соотношениях между углами и сторонами треугольника и других геометрических фигур. Историки
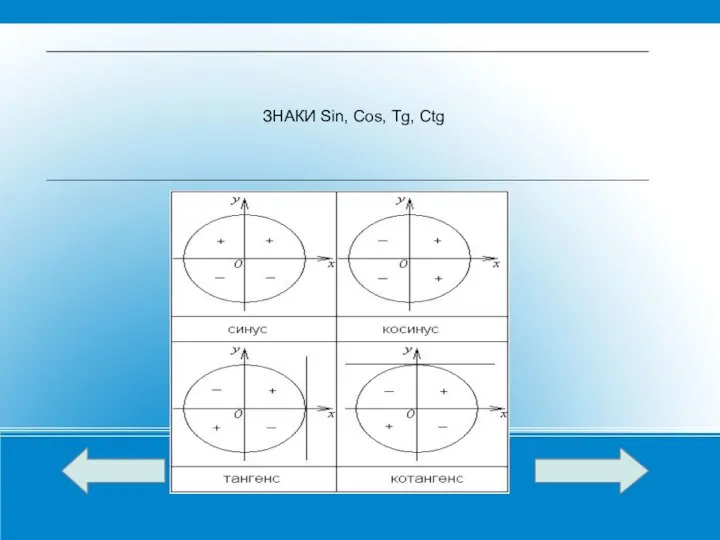
- 4. ЗНАКИ Sin, Cos, Tg, Ctg
- 5. Тригонометрические функции углов вида (п/2)k ± a , где k – Z, могут быть выражены через
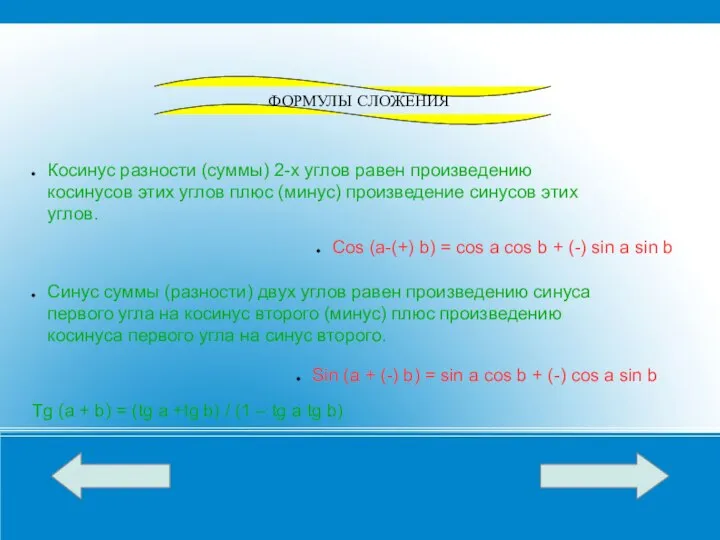
- 6. Косинус разности (суммы) 2-х углов равен произведению косинусов этих углов плюс (минус) произведение синусов этих углов.
- 7. Sin a + (-) sin b = 2 sin ((a + (-) b)/2) cos ((a –
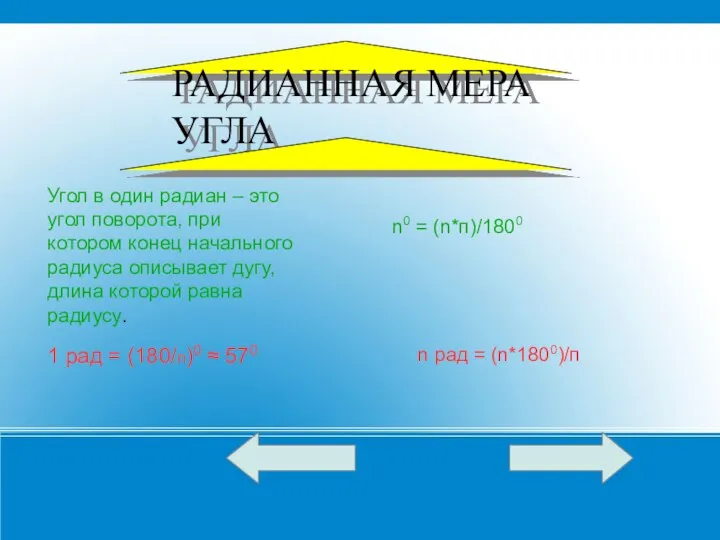
- 8. 1 рад = (180/п)0 ≈ 570 Угол в один радиан – это угол поворота, при котором
- 9. Sin 2a = 2 sin a cos a 1 + cos 2a = 2 cos2 a
- 11. Скачать презентацию




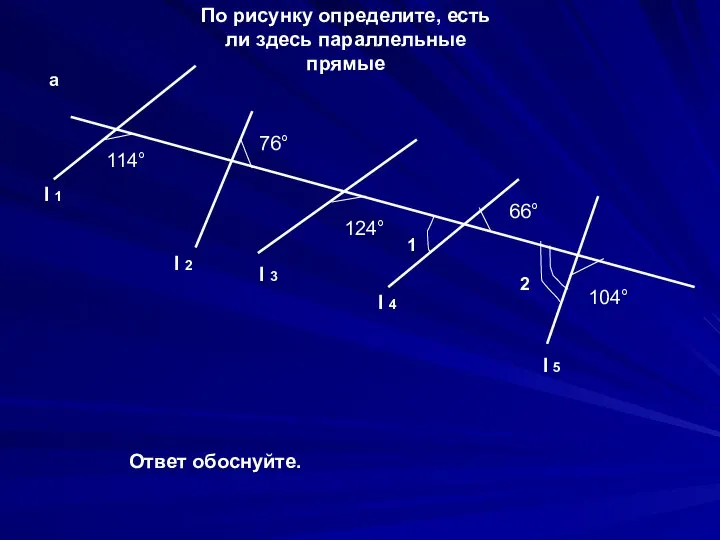 Параллельные прямые
Параллельные прямые Построение желаемой ЛАЧХ разомкнутой системы в частотном методе синтеза корректирующего звена
Построение желаемой ЛАЧХ разомкнутой системы в частотном методе синтеза корректирующего звена Деление с остатком
Деление с остатком Деление на трехзначное число
Деление на трехзначное число Решение тригонометрических уравнений
Решение тригонометрических уравнений Распределительное свойство умножения
Распределительное свойство умножения Несобственные интегралы. Геометрические приложения определенного интеграла
Несобственные интегралы. Геометрические приложения определенного интеграла Основные постулаты
Основные постулаты Тренажёр. Таблица умножения
Тренажёр. Таблица умножения Одночлены. Обобщающий урок
Одночлены. Обобщающий урок Параллельное и последовательное соединения
Параллельное и последовательное соединения Презентация на тему Расстояние от точки до прямой
Презентация на тему Расстояние от точки до прямой  Таблица умножения на 3
Таблица умножения на 3 Математика. Числа до 20
Математика. Числа до 20 Как построить график функции y=f(x)+m, если известен график функции y=f(x)
Как построить график функции y=f(x)+m, если известен график функции y=f(x) Час занимательной математики. 5 класс
Час занимательной математики. 5 класс Математические ребусы
Математические ребусы Определение стоимости проезда пассажира на железнодорожном транспорте. Задания
Определение стоимости проезда пассажира на железнодорожном транспорте. Задания Решение задач по теме Параллелограмм
Решение задач по теме Параллелограмм Степень числа
Степень числа Свойства параллельных плоскостей (10 класс)
Свойства параллельных плоскостей (10 класс) Два обыкновенных дифференциальных уравнения
Два обыкновенных дифференциальных уравнения Дифференциальное исчисление
Дифференциальное исчисление Жили-были числа
Жили-были числа Цифра 3
Цифра 3 Геометрия вокруг нас
Геометрия вокруг нас Матрицы. Основные понятия
Матрицы. Основные понятия Аксиомы стереометрии и их следствия
Аксиомы стереометрии и их следствия