Презентация на тему Первообразная 11 класс

Первообразная
Функция F(x) называется первообразной для функции f(x) на данном промежутке, если для любого x из этого промежутка F’(x) = f(x).
Пример:
Первообразной для функции f(x)=x на всей числовой оси является F(x)=x2/2, поскольку (x2/2)’=x.

Основное свойство первообразных
Если F(x) – первообразная функции f(x), то и функция F(x)+C, где C – произвольная постоянная, также является первообразной функции f(x).
Графики всех первообразных данной функции f(x) получаются из графика какой-либо одной первообразной параллельными переносами вдоль оси y.
Геометрическая интерпретация

Неопределенный интеграл
Совокупность всех первообразных данной функции f(x) называется ее неопределенным интегралом и обозначается :
,
где C – произвольная постоянная.

Правила интегрирования

Определенный интеграл
В декартовой прямоугольной системе координат XOY фигура, ограниченная осью OX, прямыми x=a, x=b (a

Определенный интеграл
Вычислим площадь криволинейной трапеции. Разобьем отрезок [a;b] на n равных частей. Проведем через полученные точки прямые, параллельные оси OY. Заданная криволинейная трапеция разобьется на n частей. Площадь всей трапеции приближенно равна сумме площадей столбиков.
по определению , его называют
определенным интегралом от функции
y=f(x) по отрезку [a;b] и обозначают так:

Связь между определенным интегралом и первообразной
(Формула Ньютона - Лейбница)
Для непрерывной функции
где F(x) – первообразная функции f(x).

Основные свойства определенного интеграла

Основные свойства определенного интеграла

Геометрический смысл
определенного интеграла
Площадь криволинейной трапеции, ограниченной графиком непрерывной положительной на промежутке [a;b] функции f(x), осью x и прямыми x=a и x=b:

Геометрический смысл
определенного интеграла
Площадь криволинейной трапеции, ограниченной графиком непрерывной отрицательной на промежутке [a;b] функции f(x), осью x и прямыми x=a и x=b:

Геометрический смысл
определенного интеграла
Замечание: Если функция изменяет знак на промежутке [a;b] , то

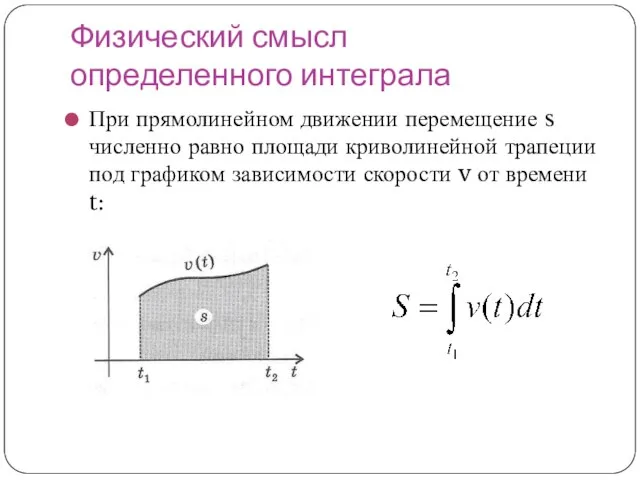
Физический смысл
определенного интеграла
При прямолинейном движении перемещение s численно равно площади криволинейной трапеции под графиком зависимости скорости v от времени t:

с помощью определенного интеграла
Вычисление площадей и объемов

Площадь фигуры,
Ограниченной графиками непрерывных функций y=f(x) и y=g(x) таких, что
для любого x из [a;b], где a и b – абсциссы точек пересечения графиков функций: