Содержание
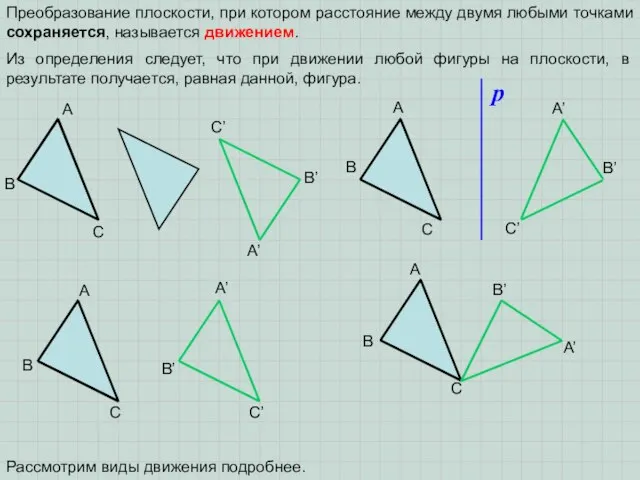
- 2. Преобразование плоскости, при котором расстояние между двумя любыми точками сохраняется, называется движением. Из определения следует, что
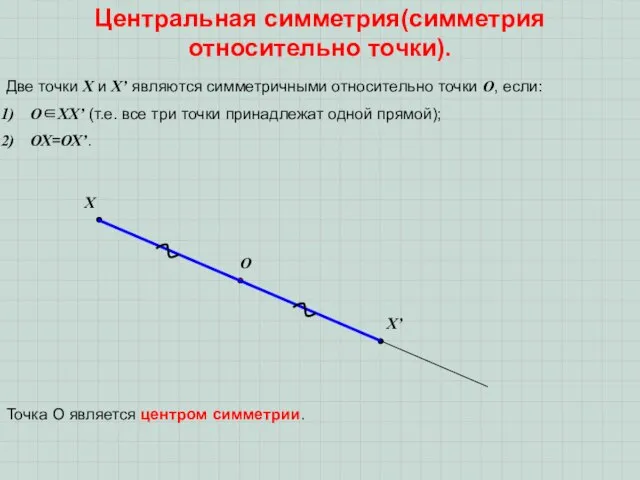
- 3. Центральная симметрия(симметрия относительно точки). Две точки Х и Х’ являются симметричными относительно точки О, если: О∈ХХ’
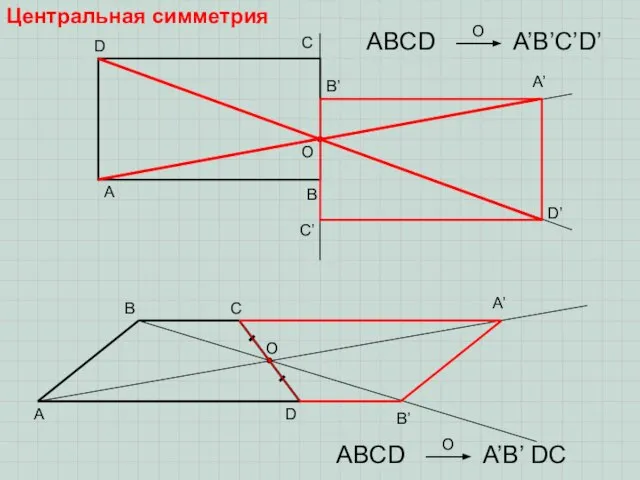
- 4. A B C D A’ B’ C’ D’ O A B C D A’ B’ O
- 5. Если при центральной симметрии фигура отображается сама в себя, то она является центрально-симметричной фигурой. A B
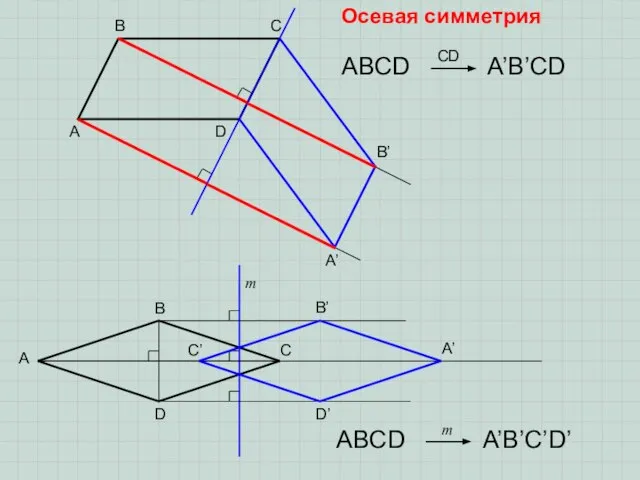
- 6. Осевая симметрия(симметрия относительно прямой). Две точки Х и Х’ являются симметричными относительно прямой р, если: р
- 7. A B C D A’ B’ ABCD A’B’CD CD m A B C D A’ B’
- 8. Если при симметрии относительно прямой фигура отображается сама в себя, то она имеет ось симметрии. A
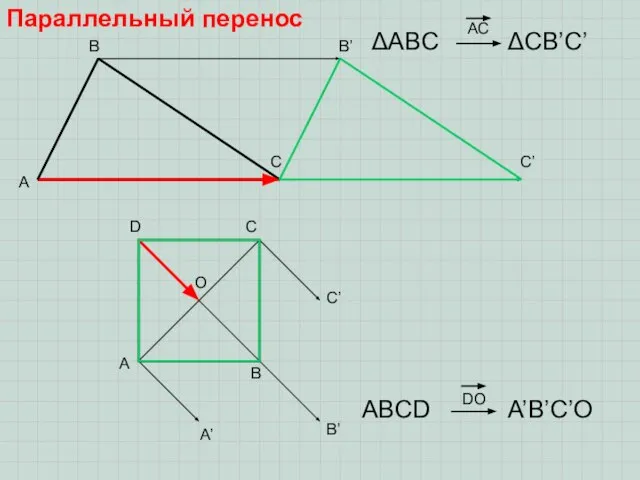
- 9. Параллельный перенос Х Х’ При этом преобразовании плоскости все точки фигуры перемещаются в одном направлении на
- 10. A B C B’ C’ ΔABC ΔCB’C’ AC A B C D O A’ B’ C’
- 11. Поворот Х Х’ О Чтобы выполнить поворот фигуры необходимо задать: 1) центр поворота, 2) направление поворота
- 13. Скачать презентацию





 Одночлен. Умножение
Одночлен. Умножение Первый признак равенства треугольников
Первый признак равенства треугольников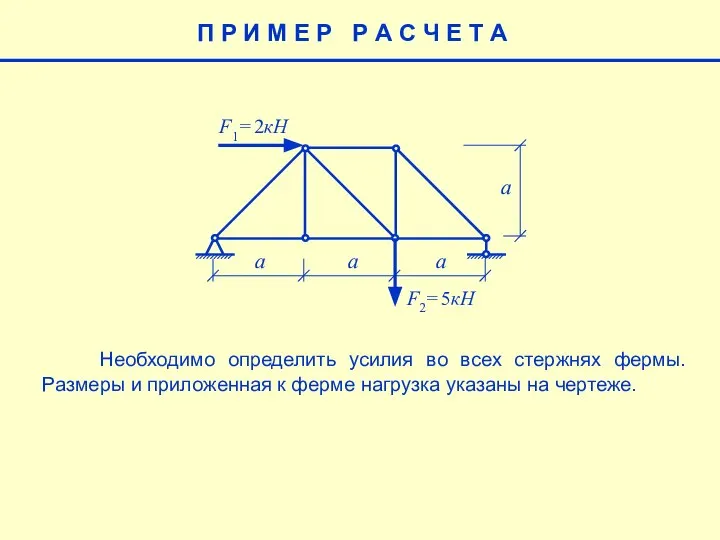 Методы расчета ферм
Методы расчета ферм Теория динамических систем
Теория динамических систем Презентация на тему Логарифмическая линия в ЕГЭ - 2011
Презентация на тему Логарифмическая линия в ЕГЭ - 2011  Конфетное вычитание
Конфетное вычитание Проект Математическая вертикаль. Геометрия. 8 класс
Проект Математическая вертикаль. Геометрия. 8 класс I признак подобия треугольников
I признак подобия треугольников Решение треугольников
Решение треугольников Примеры арифметических операций при помощи стандартных функций
Примеры арифметических операций при помощи стандартных функций Презентация на тему Арифметические действия с дробями
Презентация на тему Арифметические действия с дробями  Знакомство с линиями чертежа. Наклонная
Знакомство с линиями чертежа. Наклонная Счет
Счет Первообразная и интеграл
Первообразная и интеграл Рациональные числа 6 класс - Презентация по математике_
Рациональные числа 6 класс - Презентация по математике_ Набор инсулина в шприц
Набор инсулина в шприц Занимательная математика
Занимательная математика Основы математического моделирования. Лекция 2
Основы математического моделирования. Лекция 2 Презентация на тему Функция у=кх2 ,ее свойства и график
Презентация на тему Функция у=кх2 ,ее свойства и график  Основные этапы исследования элементарных функций
Основные этапы исследования элементарных функций Бесконечность
Бесконечность Чирмешән муниципаль районы Лашман урта гомумбелем бирү мәктәбе
Чирмешән муниципаль районы Лашман урта гомумбелем бирү мәктәбе двугранный угол. перпендикулярные плоскости. признак
двугранный угол. перпендикулярные плоскости. признак Арифметический корень степени n
Арифметический корень степени n Презентация на тему ГЕОМЕТРИЧЕСКИЕ ТЕЛА И ПЛОСКИЕ ФИГУРЫ
Презентация на тему ГЕОМЕТРИЧЕСКИЕ ТЕЛА И ПЛОСКИЕ ФИГУРЫ  Сравнение двух прогрессий
Сравнение двух прогрессий Задачи на движение
Задачи на движение Координаты вокруг нас
Координаты вокруг нас