Содержание
- 2. ДВИЖЕНИЯ Образуют специальный класс преобразований, играющих особую роль в различных науках и их приложениях и широко
- 3. ДВИЖЕНИЕ или ПЕРЕМЕЩЕНИЕ - это преобразование плоскости, сохраняющее расстояния
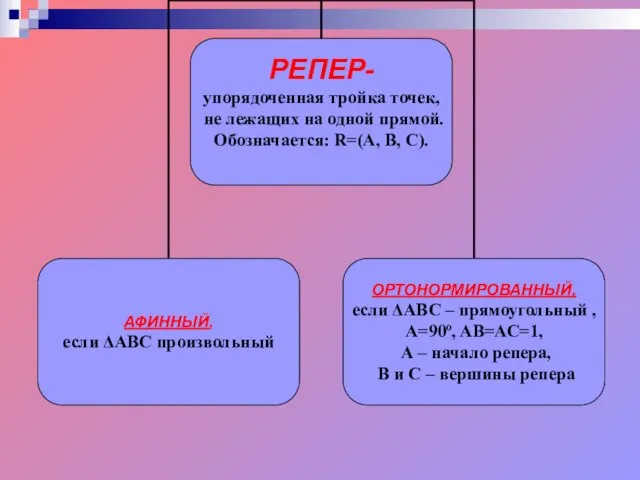
- 5. При движении репер R, образованный точками A, В, С, переходит в репер R', образованный точками A',
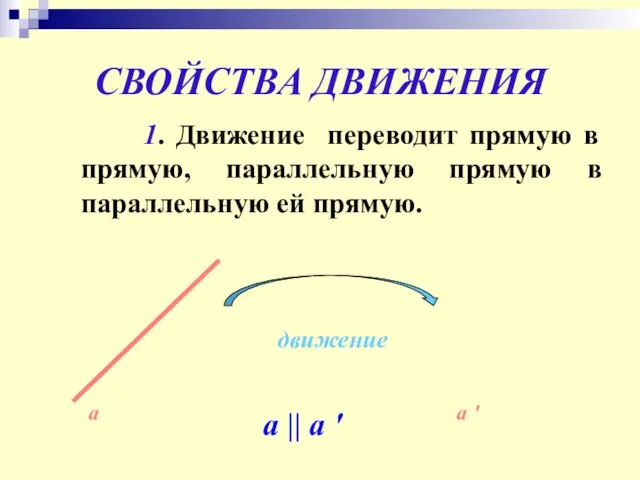
- 6. СВОЙСТВА ДВИЖЕНИЯ 1. Движение переводит прямую в прямую, параллельную прямую в параллельную ей прямую. а движение
- 7. СВОЙСТВА ДВИЖЕНИЯ 2. Движение переводит полуплоскость с границей A в полуплоскость c границей А', где А'
- 8. СВОЙСТВА ДВИЖЕНИЯ 3. Движение сохраняет простое отношение трех точек прямой. А В С λ =AC :
- 9. СВОЙСТВА ДВИЖЕНИЯ 4. Движение сохраняет отношение «лежать между». 5. Движение переводит отрезок AB в отрезок A'B'.
- 10. СВОЙСТВА ДВИЖЕНИЯ 6. Движение переводит угол в равный ему угол, луч в луч A A1 A=
- 11. СВОЙСТВА ДВИЖЕНИЯ 7. Движение переводит взаимно перпендикулярные прямые во взаимно перпендикулярные прямые а b a' b'
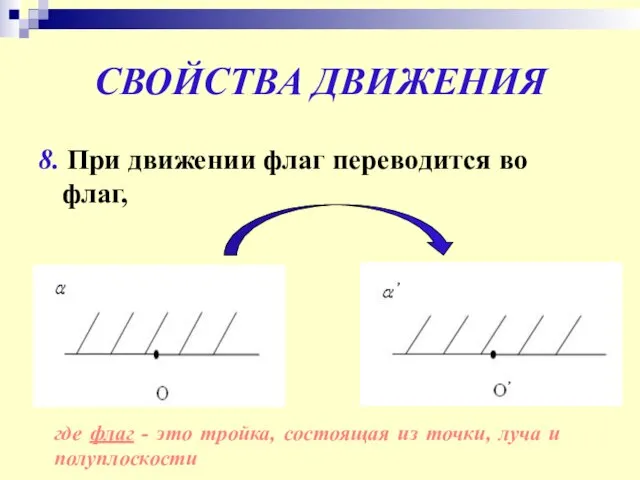
- 12. СВОЙСТВА ДВИЖЕНИЯ 8. При движении флаг переводится во флаг, где флаг - это тройка, состоящая из
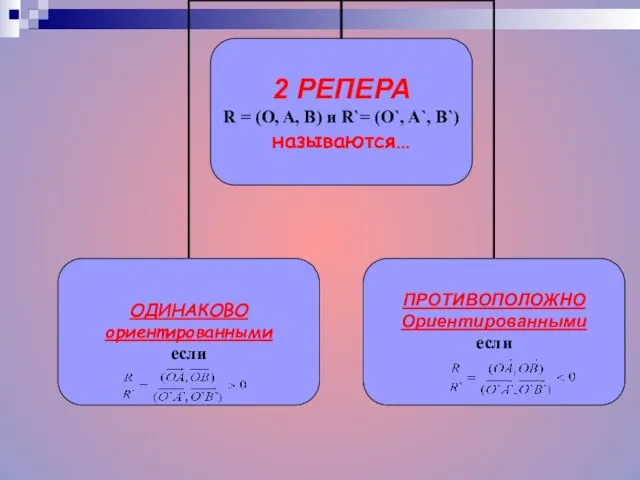
- 14. Преобразование точек плоскости сохраняет ориентацию плоскости или меняет ориентацию плоскости, если любой репер и его образ
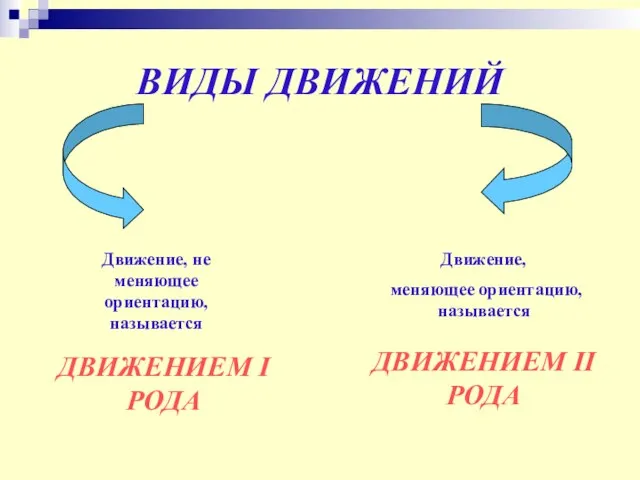
- 15. ВИДЫ ДВИЖЕНИЙ Движение, не меняющее ориентацию, называется ДВИЖЕНИЕМ I РОДА Движение, меняющее ориентацию, называется ДВИЖЕНИЕМ II
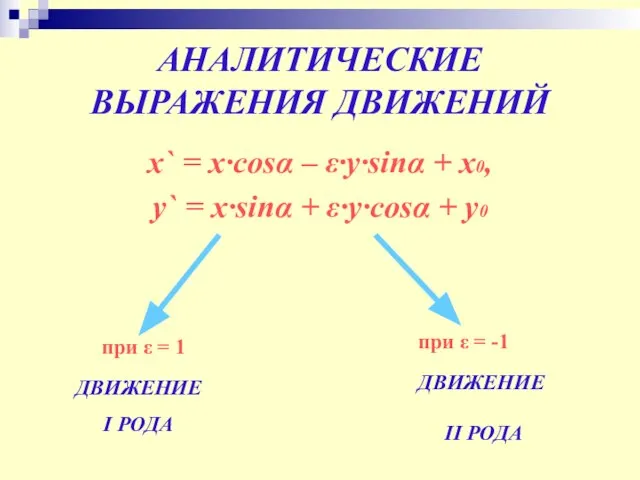
- 16. АНАЛИТИЧЕСКИЕ ВЫРАЖЕНИЯ ДВИЖЕНИЙ x` = x∙cosα – ε∙y∙sinα + x0, y` = x∙sinα + ε∙y∙cosα +
- 17. ДВИЖЕНИЕ I РОДА 1. Поворот на угол А М М1 Аналитические выражения: x` = x∙cosα –
- 18. ДВИЖЕНИЕ I РОДА 2. а)Параллельный перенос на Аналитические выражения: x` = x+х0 y` =y б) Параллельный
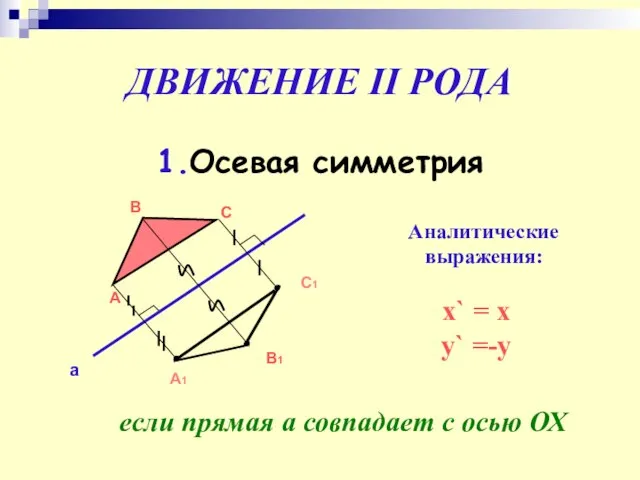
- 19. ДВИЖЕНИЕ II РОДА 1.Осевая симметрия А В С а С1 А1 В1 Аналитические выражения: x` =
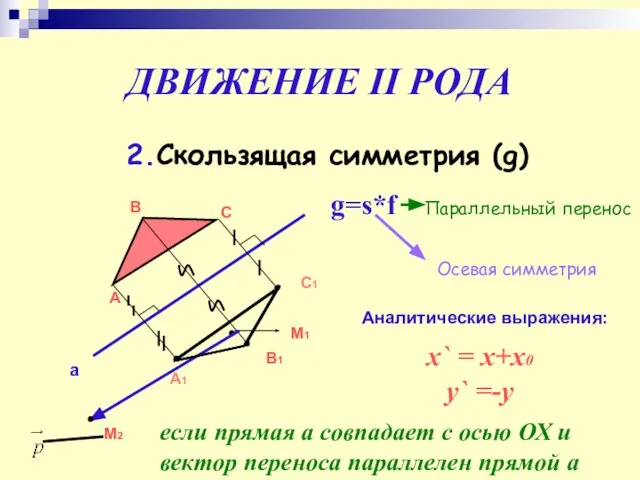
- 20. ДВИЖЕНИЕ II РОДА 2.Скользящая симметрия (g) А В С а С1 А1 В1 g=s*f Осевая симметрия
- 21. ПРЕОБРАЗОВАНИЕ ПОДОБИЯ Преобразование плоскости называется преобразованием подобия, если существует k > 0, такое что для любых
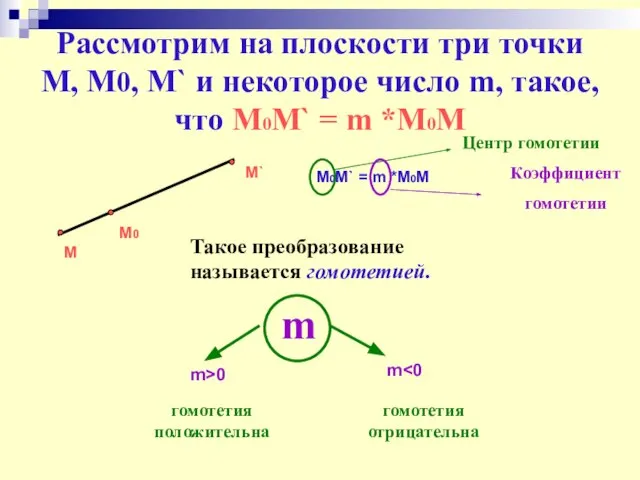
- 22. Рассмотрим на плоскости три точки М, М0, M` и некоторое число m, такое, что М0M` =
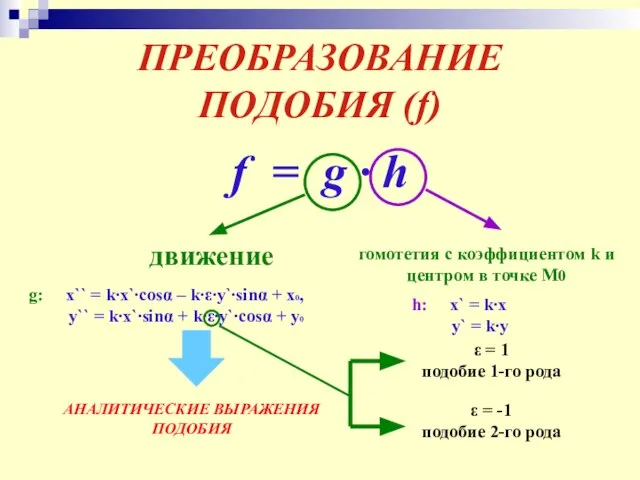
- 23. ПРЕОБРАЗОВАНИЕ ПОДОБИЯ (f) f = g ∙ h движение гомотетия с коэффициентом k и центром в
- 24. ПОДОБИЕ I РОДА Аналитические выражения: x` = k∙x∙cosα – k∙y∙sinα + x, y` = k∙y∙sinα +
- 25. 2. Параллельный перенос на О О1 Аналитические выражения: x` = k∙x+ x0, y` = k∙y+ y0
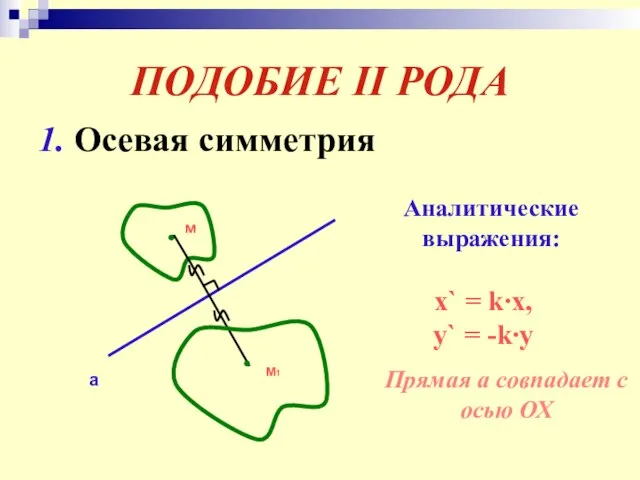
- 26. ПОДОБИЕ II РОДА 1. Осевая симметрия м а М1 Аналитические выражения: x` = k∙x, y` =
- 27. ПОДОБИЕ II РОДА 2. Скользящая симметрия x y М М1 М’ Аналитические выражения: x` = k∙x+x0,
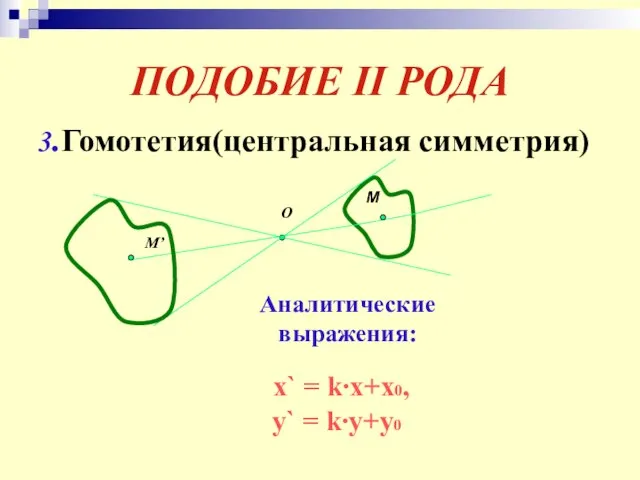
- 28. ПОДОБИЕ II РОДА 3.Гомотетия(центральная симметрия) О М М’ Аналитические выражения: x` = k∙x+x0, y` = k∙y+y0
- 30. Скачать презентацию















 Одночлен. Умножение
Одночлен. Умножение Первый признак равенства треугольников
Первый признак равенства треугольников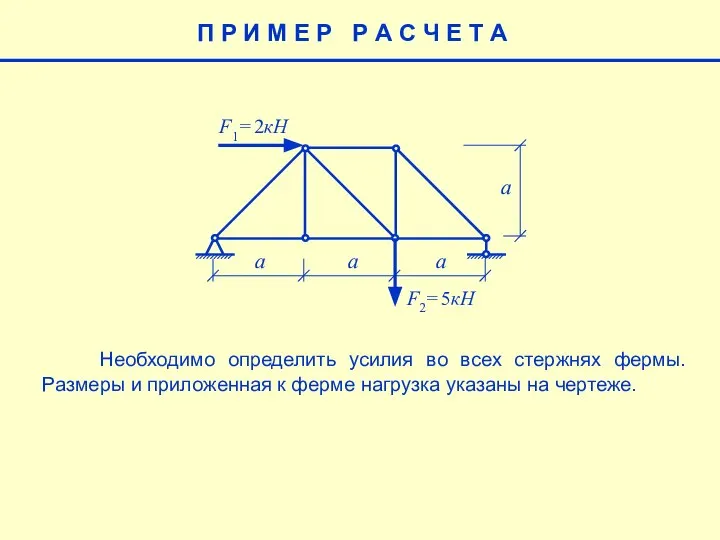 Методы расчета ферм
Методы расчета ферм Теория динамических систем
Теория динамических систем Презентация на тему Логарифмическая линия в ЕГЭ - 2011
Презентация на тему Логарифмическая линия в ЕГЭ - 2011  Конфетное вычитание
Конфетное вычитание Проект Математическая вертикаль. Геометрия. 8 класс
Проект Математическая вертикаль. Геометрия. 8 класс I признак подобия треугольников
I признак подобия треугольников Решение треугольников
Решение треугольников Примеры арифметических операций при помощи стандартных функций
Примеры арифметических операций при помощи стандартных функций Презентация на тему Арифметические действия с дробями
Презентация на тему Арифметические действия с дробями  Знакомство с линиями чертежа. Наклонная
Знакомство с линиями чертежа. Наклонная Счет
Счет Первообразная и интеграл
Первообразная и интеграл Рациональные числа 6 класс - Презентация по математике_
Рациональные числа 6 класс - Презентация по математике_ Набор инсулина в шприц
Набор инсулина в шприц Занимательная математика
Занимательная математика Основы математического моделирования. Лекция 2
Основы математического моделирования. Лекция 2 Презентация на тему Функция у=кх2 ,ее свойства и график
Презентация на тему Функция у=кх2 ,ее свойства и график  Основные этапы исследования элементарных функций
Основные этапы исследования элементарных функций Бесконечность
Бесконечность Чирмешән муниципаль районы Лашман урта гомумбелем бирү мәктәбе
Чирмешән муниципаль районы Лашман урта гомумбелем бирү мәктәбе двугранный угол. перпендикулярные плоскости. признак
двугранный угол. перпендикулярные плоскости. признак Арифметический корень степени n
Арифметический корень степени n Презентация на тему ГЕОМЕТРИЧЕСКИЕ ТЕЛА И ПЛОСКИЕ ФИГУРЫ
Презентация на тему ГЕОМЕТРИЧЕСКИЕ ТЕЛА И ПЛОСКИЕ ФИГУРЫ  Сравнение двух прогрессий
Сравнение двух прогрессий Задачи на движение
Задачи на движение Координаты вокруг нас
Координаты вокруг нас