Первый признак равенства треугольников

Аксиома – греческое слово, означает
«достоинство», «уважение», «авторитет».
Первоначально имело смысл
«самоочевидная истина».
Термин впервые встречается
у Аристотеля и перешел в
математику от философов
Древней Греции.

Аксиома –
это утверждение, содержащиеся в формулировках основных свойств простейших фигур, не доказываются и называются аксиомами.

Аксиомы
Через любые две точки можно провести прямую и при том только одну.
Из трех точек на прямой одна и только одна лежит между двумя другими.
На любом луче от его начала можно отложить отрезок, равный данному и при том только один.
От любого луча в заданную сторону можно отложить угол, равный данному и при том только один.

Теорема – греческое слово, означает
«зрелище», «представление».
В математике греков это слово стало
употребляться в смысле «истина, доступная созерцанию».
Само греческое слово происходит от слова «рассматриваю», «обдумываю».
Слово, как математический термин, встречается у Аристотеля.

Правильность утверждения о свойстве той или иной геометрической фигуры устанавливается путем рассуждения – называется доказательством.
Само утверждение, которое доказывается, называется теоремой.

Устройство теоремы
Если «УСЛОВИЕ», то «ЗАКЛЮЧЕНИЕ».
дано доказать

Первый признак равенства треугольников.
Теорема. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
В математике каждое утверждение, справедливость которого устанавливается путем рассуждений, называется теоремой
Доказать: ∆АВС=∆А1В1С1
Наложим ∆ А1В1С1 на треугольник ∆ АВС.
Доказательство:
Поскольку АВ=А1В1, АС=А1С1, то сторона АВ совместится со стороной А1В1, а сторона АС – со стороной А1С1; в частности, совместятся точки В и В1, С и С1.
Следовательно, совместятся стороны ВС и В1С1.

Вопросы
Назовите все возможные обозначения данного треугольника.
Укажите сторону, лежащую против угла С.
Укажите угол, лежащий против стороны СМ.
Укажите углы, прилежащие к стороне ЕС.
Укажите угол между сторонами ЕС и ЕМ.

Вопросы.
На рисунке изображены равные треугольники АВС и РОТ.
Укажите соответственно равные элементы этих треугольников.

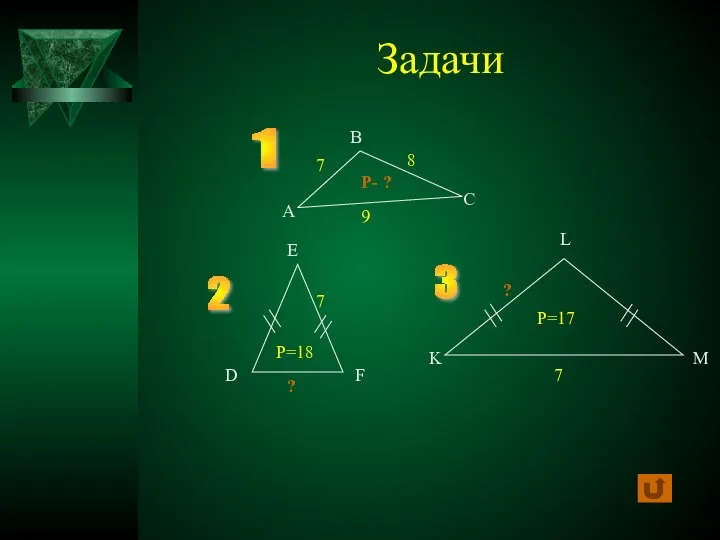
Задачи
1
2
3
P=17