Теория динамических систем

ДС
Под динамической системой понимают любой процесс или объект, для которого характерно:
однозначно определенное состояние как совокупности некоторых величин в данный момент времени;
задан закон (эволюция), который описывает изменения начального состояния с течением времени

Число степеней свободы – наименьшее число независимых величин (координат), необходимых для однозначного определения состояния системы.
Фазовое пространство – пространство на координатных осях которого отложены значения переменных состояния системы: х1, х2, …, хn, называемых фазовыми переменными.
Изображающая точка – точка, расположенная на фазовом пространстве.
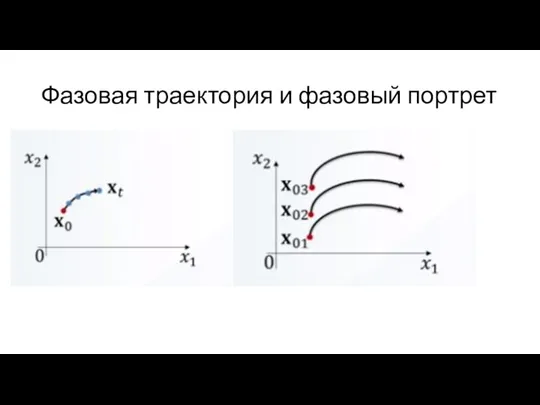
Фазовая траектория – совокупность изображающих точек.
Совокупность фазовых траекторий при различных начальных условиях называется фазовым портретом системы

Одномерное и двумерное фазовое
пространство

Фазовая траектория и фазовый портрет

Формальное определение динамической системы
фазовое пространство Х, образующее полное метрическое пространство;
множество моментов времени Т;
оператор эволюции Et – некоторое отображение, которое каждому состоянию х0 € Х в начальный момент времени t0 € T однозначно ставит в соответствие некоторое состояния xt € Х в любой другой момент времени t € T.

Классификация динамических систем
с непрерывным временем (континуальные системы), т.е. системы, которые задаются дифференциальными уравнениями:
ẋ = F(x)
системы с дискретным временем, N – мерные отображения, например, геометрическая прогрессия:
xn+1 = f (xn)
по виду оператора эволюции:
- линейные:
Et (x + x') = Et (x) + Et (x')
Et (α·x) = α Et (x)

Классификация динамических систем
- нелинейные:
Et (x + x') ≠ Et (x) + Et (x')
автономные, т.е. вектор F(x) зависит только от x и не зависит от времени:
ẋ = F(x)
неавтономные т.е. вектор F(x) зависит не только от координаты x, но зависит от времени:
ẋ = F (x, t)

Классификация динамических систем
детерминированные – это все рассмотренные выше системы, когда нет шумов, случайных слагаемых.
случайные динамические системы – это автономные динамические системы, в которых есть шум определенного вида εt
ẋ = F(x) + εt

Устойчивость решения динамических систем
Устойчивость по Ляпунову. Решение динамической системы устойчиво по Ляпунову, если для любого ε > 0 найдется число δ (ε) > 0, такое, что если ||х0 – π0|| < δ, то ||х (t) – π (t)|| < ε для всех t ≥ 0.
Таким образом, для двухмерной динамической системы любое решение, которое начинается в δ-окрестности точки π0 остается внутри трубки с максимальным радиусом ε при всех t ≥ 0

Устойчивость решения динамических систем
Асимптотическая устойчивость. Если решение динамической системы устойчиво не только по Ляпунову, но и удовлетворяет соотношению
lim ||х (t) – π (t|| = 0 при условии t → ∞ и ||х0 – π0|| < δ, то решение является асимптотически устойчивым.
Таким образом, все решения, достаточно близкие к π0 в начальный момент времени постепенно сходятся к π (t) на больших временах. И если решение асимптотически устойчиво, то оно устойчиво и по Ляпунову.

Устойчивость решения динамических систем
Экспоненциальная устойчивость. Если решение динамической системы устойчиво не только по Ляпунову, но из условия ||х0 – π0|| < δ следует, что ||х (t) – π (t)|| ≤ α ||х0 – π0||е-βt для всех t ≥ 0, то решение является асимптотически устойчивым.
Все решения, близкие к π0 в начальный момент времени сходятся к π (t) с большей или равной экспоненциальной скоростью. В отличии от предыдущего случая экспоненциальная устойчивость отличается лишь скоростью сходимости решения.

Одномерные динамические системы
Одномерные динамические системы – это динамические системы на прямой или динамические системы с одной с одной степенью свободы.
Рассмотрим динамическую систему первого порядка, математическая модель которой задана в следующем виде:
ẋt = F (xt), xt = x (t), t ≥ 0

1. Аналитический подход решения задачи Коши
Формулировка задачи Коши: известен закон эволюции и начальное состояние системы, требуется найти решение дифференциального уравнения или интеграл.
Это самый мощный подход к анализу динамических систем. Но есть один недостаток к анализу нелинейных – не всегда удается получить аналитическое решение задачи.

2. Численное решение задачи Коши
это численный эксперимент, применение численных методов. Однако не всегда удается получить фазовый портрет, так как коэффициенты динамической системы принимают непрерывный набор численных значений.
Когда пытаются построить фазовую траекторию, теоретически нужно рассмотреть все возможные параметры решений, чтобы не упустить важные параметры, например, бифуркацию.
Иногда этот подход применяют как дополнение к первому или третьему подходу.

3. Качественный анализ или метод фазовых траекторий
Позволяет по заданному закону эволюции получить фазовый портрет.
Применим как к линейным, так и к нелинейным динамическим системам.
Основное достоинство этого метода – глобальная картина поведения фазовых траекторий. Зная фазовый портрет можно однозначно определить поведение всей динамической системы.
Есть и ограничения, связанные с числом степеней свободы.
Для одномерных, двухмерных и трехмерных можно получить решение, а для четырехмерных и выше степеней свободы это становиться затруднительно.

Качественный анализ динамических систем
Задача Коши в рамках качественного анализа формулируется следующим образом.
Входные данные:
ẋt = F (x0, α),
где
xt € Rn – вектор длин переменных;
α € Rm – вектор параметров системы.
Необходимо найти компоненты (координаты) α при которых:
равновесие системы является устойчивым;
происходит локальная бифуркация в системе.

Алгоритм анализа одномерных динамических систем ẋt = F (xt)
Шаг 1. Решить уравнение F (xt) и определить стационарные (фиксированные, равновесные) точки х* Их может быть одна, две или три, все зависит от функции

Алгоритм анализа одномерных динамических систем ẋt = F (xt)
Шаг 2. Изобразить фазовую траекторию ẋt = F (xt) на плоскости х0ẋ. Особенность фазовой траектории в том, что она пересекает ось х в равновесных точках.

Алгоритм анализа одномерных динамических систем ẋt = F (xt)
Шаг 3. Классифицировать стационарные точки, т е. определить какие точки являются асимптотически устойчивые, какие неустойчивые.
Если в некоторой окрестности х* фазовая траектория убывает, то х* является асимптотически устойчивой точкой или аттрактором.
Неустойчивая точка – это репеллер, фазовая траектория в их окрестности возрастает.

Поведение решений динамической системы вблизи аттрактора и репеллеров

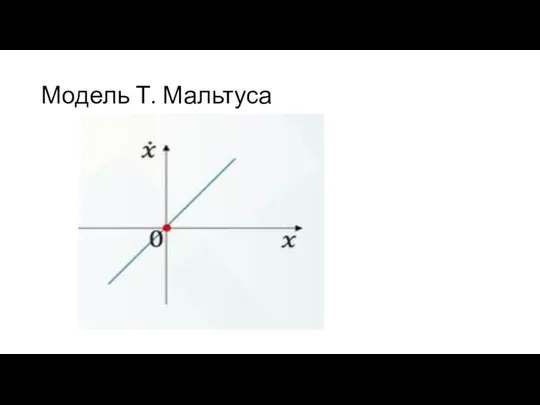
Модель Т. Мальтуса
Т. Мальтус – известный демограф, экономист. Он показал в своем труде «О росте народонаселения», что с увеличением населения, ростом популяции истощаются ресурсы.
Адаптируем модель Мальтуса к моделированию роста производства продукции без ограничения на потребление ресурсов. Математическая модель представлена ниже:
ẋt = αxt,
где
xt ≥ 0 – количество продукции;
α > 0 – постоянный темп роста продукции.

Модель Т. Мальтуса

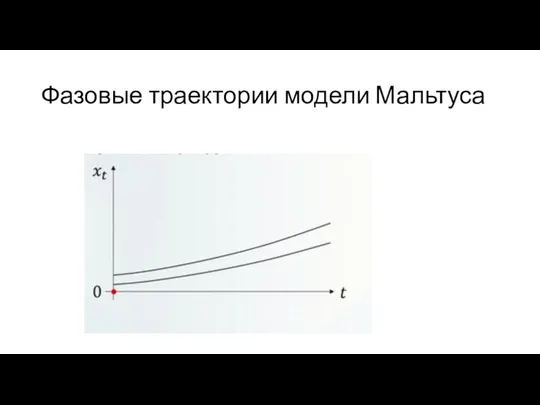
Фазовые траектории модели Мальтуса

Выводы:
Во-первых, неограниченное потребление ресурса приводит к неограниченному производству продукта. В реальной ситуации этого конечно же не происходит, следовательно, модель является неадекватной и необходимо перейти к другой модели.
Во-вторых, неограниченное производство приводит к истощению ресурсов.

Модель Ферхюльста
Математическая модель роста производства продукции с учетом ограничения на потребление ресурсов представлена ниже:
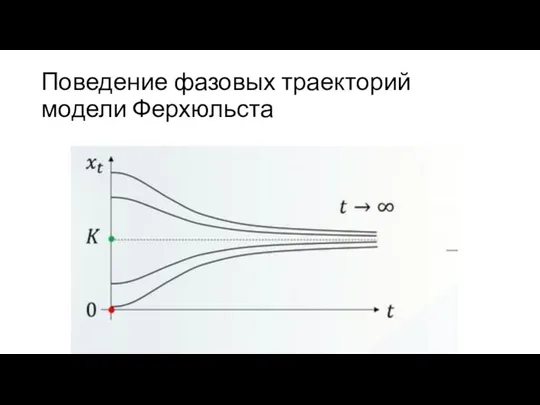
ẋt = α‧xt (1 - xt / К),
где
xt ≥ 0 – количество продукции;
α > 0 – постоянный темп роста продукции;
К > 0 – максимальное количество продукции, определяемое доступным ресурсом.

Фазовая плоскость модели Ферхюльста

Поведение фазовых траекторий модели Ферхюльста