Содержание
- 2. Содержание Формулы сокращенного умножения Вынесение общего множителя за скобки Способ группировки Разложение квадратного трехчлена на множители
- 3. Формулы сокращенного умножения
- 4. 1. Квадрат суммы Доказательство: К таблице К содержанию
- 5. 2. Квадрат разности К таблице К содержанию Доказательство:
- 6. 3. Разность квадратов К таблице К содержанию Доказательство:
- 7. 4. Куб суммы К таблице К содержанию Доказательство:
- 8. 5. Куб разности К таблице К содержанию Доказательство:
- 9. 6. Сумма кубов К таблице К содержанию Доказательство:
- 10. 7. Разность кубов К таблице К содержанию Доказательство:
- 11. Вынесение общего множителя за скобки Из каждого слагаемого, входящего в многочлен, выносится некоторый одночлен, входящий в
- 12. Алгоритм нахождения общего множителя нескольких одночленов Найти наибольший общий делитель коэффициентов всех одночленов, входящих в многочлен,
- 13. Пример Разложить на множители: x4y3 - 2x3y2 + 5x2. Воспользуемся сформулированным алгоритмом. Наибольший общий делитель коэффициентов
- 14. Способ группировки Бывает, что члены многочлена не имеют общего множителя, но после заключения нескольких членов в
- 15. 1. Сгруппировать его члены так, чтобы слагаемые в каждой группе имели общий множитель 2. Вынести в
- 16. Для уяснения сути способа группировки рассмотрим следующий пример: разложить на множители многочлен xy–6+3x–2y
- 17. xy-6+3x-2y= =(xy-6)+(3x-2y). Группировка неудачна. Первый способ группировки:
- 18. Второй способ группировки xy-6+3x-2y=(xy+3x)+(-6-2y)= =x(y+3)-2(y+3)= =(y+3)(x-2).
- 19. xy-6+3y-2y=(xy-2y)+(-6+3x)= =y(x-2)+3(x-2)= =(x-2)(y+3). Третий способ группировки:
- 20. Как видите, не всегда с первого раза группировка оказывается удачной. Если группировка оказалась неудачной, откажитесь от
- 21. Разложение квадратного трехчлена на множители
- 22. К содержанию
- 24. Скачать презентацию




















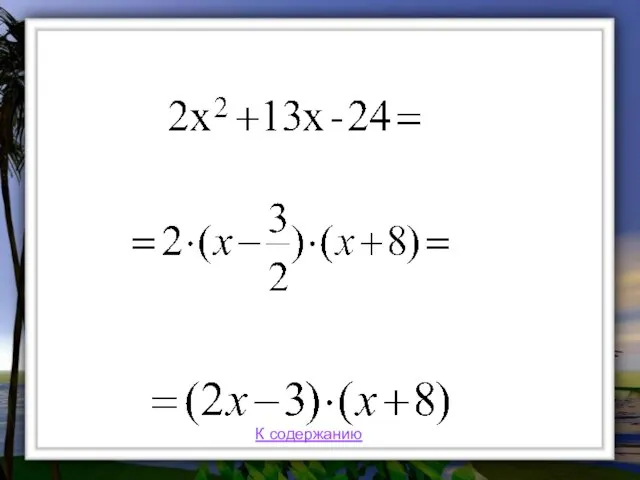
 Стереометрия. Многогранники
Стереометрия. Многогранники Таблица сложения в пределах 20
Таблица сложения в пределах 20 Умножение обыкновенных дробей
Умножение обыкновенных дробей УК Теория и примеры типовых задач. Проверка (испытание) гипотез
УК Теория и примеры типовых задач. Проверка (испытание) гипотез Анализ результатов Всероссийской олимпиады школьников по математике 2020-2021 учебного года
Анализ результатов Всероссийской олимпиады школьников по математике 2020-2021 учебного года Подготовка к контрольной работе
Подготовка к контрольной работе Дискретная математика. Повторение арифметических действий
Дискретная математика. Повторение арифметических действий Решение текстовых задач арифметическим способом
Решение текстовых задач арифметическим способом Способ группировки
Способ группировки Линейные алгоритмы
Линейные алгоритмы Деление отрицательного числа на отрицательное
Деление отрицательного числа на отрицательное Математика (1 класс)
Математика (1 класс) Построение треугольника
Построение треугольника Прямые на плоскости
Прямые на плоскости Матрицы и определители
Матрицы и определители Цикломатика графов
Цикломатика графов Пересечение поверхностей. Лекция 8
Пересечение поверхностей. Лекция 8 Векторы
Векторы Прямоугольник. Свойства прямоугольника
Прямоугольник. Свойства прямоугольника Сообщение по истории математики «Из истории позиционных систем счисления» Выполнила ученица 6 «А класса» Дивии Идегел
Сообщение по истории математики «Из истории позиционных систем счисления» Выполнила ученица 6 «А класса» Дивии Идегел Окружность и круг
Окружность и круг Кто живет под грибом
Кто живет под грибом Презентация на тему СРАВНЕНИЕ ДРОБЕЙ
Презентация на тему СРАВНЕНИЕ ДРОБЕЙ  Координаты вектора. Простейшие задачи в координатах
Координаты вектора. Простейшие задачи в координатах Симплексный метод
Симплексный метод Преобразование обыкновенных дробей в десятичные и десятичных в обыкновенные
Преобразование обыкновенных дробей в десятичные и десятичных в обыкновенные Приемы устного счета
Приемы устного счета Знакомство с линиями чертежа Замкнутая, незамкнутая
Знакомство с линиями чертежа Замкнутая, незамкнутая