Содержание
- 2. 1. В урне лежат одинаковые шары : 5 белых, 3 красных и 2 зелёных. Саша вынимает
- 3. 2. На тарелке лежат одинаковые на вид блинчики: 3 с творогом, 5 с мясом и 4
- 4. 3. В копилке находятся монеты достоинством 2 рубля – 14 штук, 5 рублей – 10 штук
- 5. 4. В коробке находятся 7 красных шаров, 13 белых шаров и 6 голубых шаров. Определите вероятность
- 6. 5. Подбрасывают три монеты. Какова вероятность того, что все монеты упадут орлом вверх? Ответ: 0,25 Решение:
- 7. 6. Подбрасывают три монеты. Какова вероятность того, что ровно одна монета упадёт орлом вверх? Ответ: 0,5
- 8. 7. На полке стоят одинаковые на вид бутылки с прозрачной жидкостью: 4 бутылки с этиловым спиртом,
- 9. 8. В пенале лежат несколько неотличающихся внешне друг от друга простых карандашей: 8 твёрдых, 12 мягких
- 10. 9. Паша наудачу выбирает двузначное число. Найдите вероятность того, что оно оканчивается на 7. Ответ: 0,1
- 11. 10. На экзамене 45 билетов, Антон не успел выучить 18 из них. Найдите вероятность того, что
- 12. 11. В конкурсе «Мисс мира» участвуют 100 девушек из разных стран, среди них 48 блондинок. Какова
- 13. 12. В полуфинале Кубка России играют четыре команды в матчах: «Спартак»(Москва) – ЦСКА(Москва), «Ростов»(Ростов-на-Дону) – «Алания»(Владикавказ).
- 14. 13. В шкафу стоят непрозрачные бутылки без надписей: 4 с соком, 3 с водой и 5
- 15. 14. На тарелке лежат одинаковые на вид пирожки:5 с мясом, 7 с картошкой и 11 с
- 16. 15. При производстве 1200 электроприборов для машин марки «Лада» только 6 оказалось бракованными. Какова вероятность того,
- 17. 16. В мешке находятся 3 белых, 4 чёрных и 5 синих шариков. Наугад вынимается один шарик.
- 18. 17. На полке стоят книги: пять детективов, семь романов и три сборника стихов. Определите вероятность того,
- 19. 18. В лотерее участвуют 40 тысяч жителей Москвы, 50 тысяч жителей Санкт-Петербурга и 30 тысяч жителей
- 20. 19. В соревнованиях по фигурному катанию участвуют пять пар из России, три пары из Канады, четыре
- 21. 20. На столе лежат 7 синих, 3 красных и 5 зелёных ручек. Найдите вероятность того, что
- 22. 21. В классе 30 человек. Для участия в субботнике случайным образом выбирают 12 учеников. Какова вероятность
- 23. 22. В тестовом задании пять вариантов ответа, из которых только один верный. Какова вероятность правильно решить
- 24. 23. В мешке находятся 2 чёрных и 3 белых шара. Наугад вытаскивают два шара. Какова вероятность
- 25. 24. В пакете с леденцами 3 леденца с апельсиновым вкусом, 4 с лимонным и 5 с
- 26. 25. В заключительном этапе велосипедной гонки участвуют равные по профессиональной квалификации спортсмены: 5 велосипедистов общества «Динамо»,
- 27. 26. В корзине лежат 7 помидоров, 6 огурцов, 12 перцев. Найдите вероятность того, что первый наугад
- 28. 27. Из города А в город В можно добраться четырьмя разными способами, а из города В
- 29. 28. Из города А в город В можно добраться поездом, самолётом и на автомобиле. Из города
- 31. Скачать презентацию




























 Число и цифра 3
Число и цифра 3 Золотое сечение. 9 класс
Золотое сечение. 9 класс Презентация по математике "Город арифметика" -
Презентация по математике "Город арифметика" -  Сумма углов геометрических фигур. Транспортир
Сумма углов геометрических фигур. Транспортир Решение примеров в пределах 10
Решение примеров в пределах 10 Производная и интеграл степенной функции с действительным показателем
Производная и интеграл степенной функции с действительным показателем Виды треугольников
Виды треугольников Роберт Гук
Роберт Гук Случаи вычитания 11-
Случаи вычитания 11- Абсолютные и относительные величины в статистике
Абсолютные и относительные величины в статистике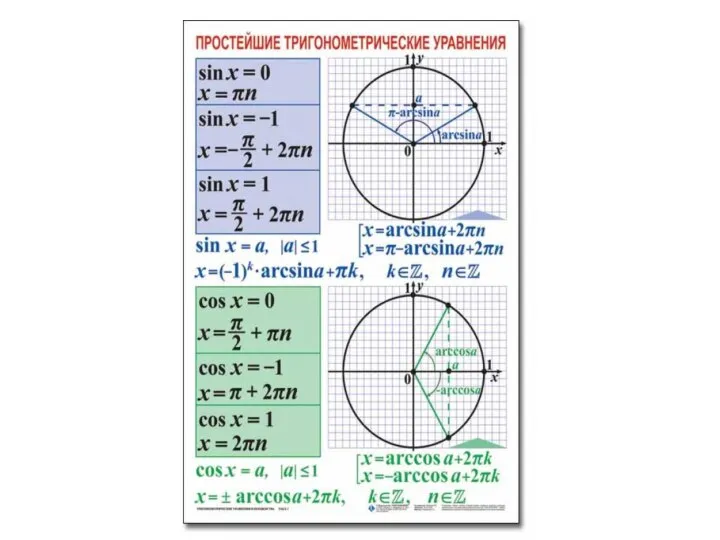 Простейшие тригонометрические уравнения
Простейшие тригонометрические уравнения Уравнение tg x =a
Уравнение tg x =a Презентация на тему Вычисление объёма цилиндра
Презентация на тему Вычисление объёма цилиндра  Л 9 Бесконечно большие функции и замечательные пределы
Л 9 Бесконечно большие функции и замечательные пределы Решение выражений и уравнений
Решение выражений и уравнений Осевая симметрия
Осевая симметрия Описательные статистики
Описательные статистики Презентация на тему Площадь многоугольников
Презентация на тему Площадь многоугольников  Степень с натуральным показателем. Применение свойств к построению графиков степенных функций. 7 класс
Степень с натуральным показателем. Применение свойств к построению графиков степенных функций. 7 класс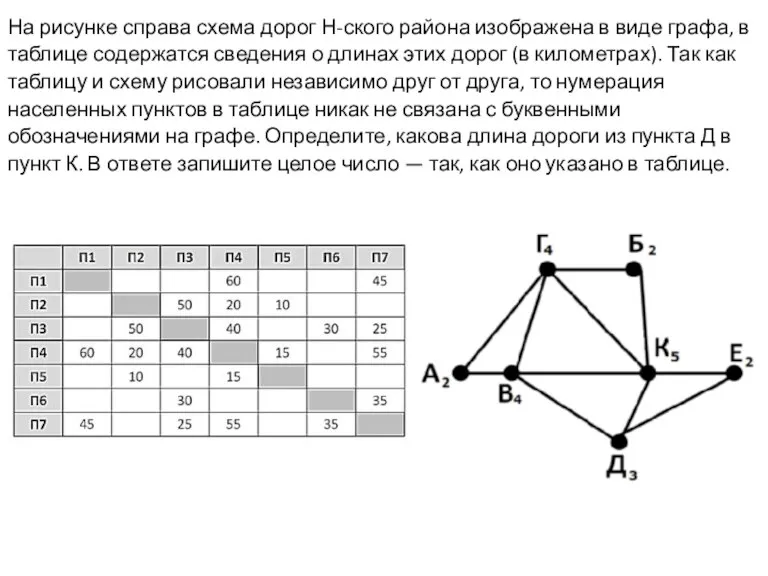 Решение задач
Решение задач Презентация на тему Иррациональные числа
Презентация на тему Иррациональные числа  Математика вокруг нас
Математика вокруг нас Презентация на тему Шкалы и координаты (5 класс)
Презентация на тему Шкалы и координаты (5 класс)  Решение задач
Решение задач Презентация на тему Математический диктант 2 класс
Презентация на тему Математический диктант 2 класс  Геометрия треугольника
Геометрия треугольника Проект-игра по геометрии Занимательная геометрия
Проект-игра по геометрии Занимательная геометрия Длина окружности,
Длина окружности,