Слайд 2Линейное уравнение.
Равенство, содержащие неизвестное число, обозначенной буквой, называется – уравнением.
Выражение, стоящее

слева от знака равенства, называется левой частью управления, а выражение стоящее справа от знака равенства, - правой частью уравнения.
Каждое слагаемое левой и правой части уравнения называется членом уравнения.
Слайд 3Корень уравнения.
Корнем уравнения называется то значение неизвестного, при котором это уравнение

обращается в верное числовое равенство.
Уравнение может иметь один корень:
3x+5=0
Несколько корней:
y(y-2)(5+2y) = 0
Бесконечно много корней:
7(x+1) = 7x+7
Уравнение может не иметь корней:
x+3=x
Слайд 4Свойства уравнений.
Решить уравнение – это значит найти все его корни или

установить что их нет.
При решении уравнений могут быть использованы свойства уравнения:
1- Корни уравнения не изменяются, если любой член уравнения перенести из одной части уравнения в другую, изменив при этом знак на противоположный.
2 – Корни уравнения не изменяются, если обе части уравнения умножить или разделить на одно и то же число, не равное нулю.
Уравнения вида ax=b, где x- неизвестное, a и b – некоторые числа, называются линейным уравнением с одним неизвестным. Решение многих уравнений сводится к решению линейных уравнений .
Слайд 5Алгоритм решения уравнения:
1- упростить левую и правую части уравнения (раскрыть скобки и

привести подобные слагаемые, если они есть);
2 – собрать в левой части уравнения все члены уравнения, содержащие неизвестное, а в правой – не содержащие неизвестное;
3- привести подобные слагаемые в обеих частях уравнения;
4- разделить обе части уравнения на коэффициент при неизвестном (если он не равен нулю).
Слайд 6Если коэффициент при неизвестном в уравнении ax=b равен нулю то;
1) a= 0;

b не равно 0 - корней нет.
2) a= 0; b=0 - бесконечное много корней (x – любое число).
Слайд 7Задание для учеников:
2(3x-4) +5 = 7-3 (2-x)
1x + 1x +3 =
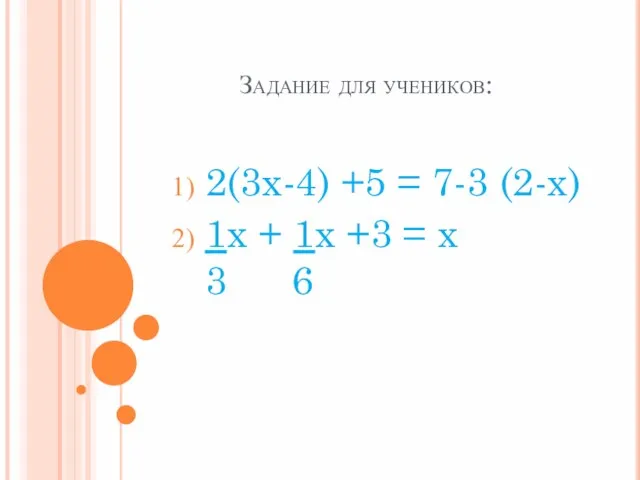
x
3 6
Слайд 8Решение №1.
А) 2(3x-4) +5=7–3(2-x)
6x-8+5=7-6+3x
6x-3x=7-6+8-5;
3x = 4
X = 4

3
X = 1 1
3 .
Слайд 9Решение №2
1x+ 1x + 3 = x;
3 6
Умножим обе части уравнения на

6.
2x+x+18 = 6x;
-3x = -18;
X = 6.
Слайд 10Для домашнего задания
Решите уравнения используя правила.
1) 2y-2 (y-8)=7
2) 5x – (x-6)

= 2(2x+3).





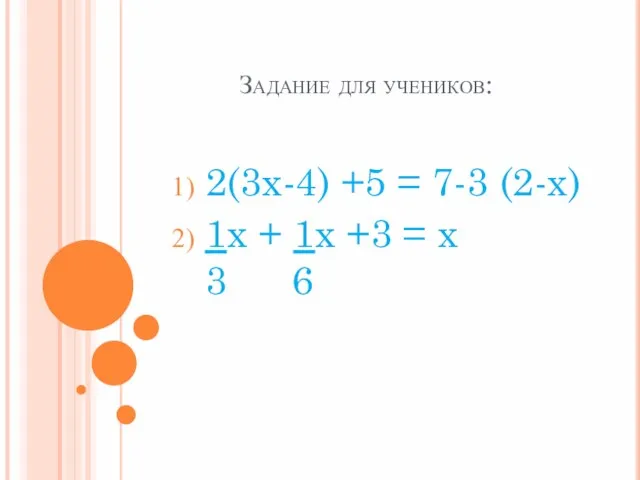



 Проценты
Проценты Параллельные прямые и плоскости
Параллельные прямые и плоскости Коэффициенты линейных функций
Коэффициенты линейных функций Основные тригонометрические тождества. Формулы приведения
Основные тригонометрические тождества. Формулы приведения Методика изучения двумерных геометрических фигур: угол, виды углов; ломаная, многоугольники и их виды
Методика изучения двумерных геометрических фигур: угол, виды углов; ломаная, многоугольники и их виды Проценты в нашей жизни. Можно ли обойтись без знаний процентов в повседневной жизни?
Проценты в нашей жизни. Можно ли обойтись без знаний процентов в повседневной жизни? Группируем слагаемые и множители
Группируем слагаемые и множители Евклидовы пространства
Евклидовы пространства Математична статистика
Математична статистика Расширение и углубление знаний учащихся о преобразованиях графиков функций
Расширение и углубление знаний учащихся о преобразованиях графиков функций Сравнение многозначных чисел. 4 класс
Сравнение многозначных чисел. 4 класс Презентация на тему ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ УРАВНЕНИЙ
Презентация на тему ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ УРАВНЕНИЙ  Интегрированный урок математики и чтения в 5 классе. Басни И.А.Крылова
Интегрированный урок математики и чтения в 5 классе. Басни И.А.Крылова Задача № 106
Задача № 106 Площадь поверхности вращения
Площадь поверхности вращения Что такое разложение многочлена на множители
Что такое разложение многочлена на множители Математика в профессии моих родителей
Математика в профессии моих родителей Вычисление определенного интеграла
Вычисление определенного интеграла delenie_s_ostatkom-_2_
delenie_s_ostatkom-_2_ Степенная функция
Степенная функция Математический анализ. Исследование функций и построение графиков. Асимптоты графика функции
Математический анализ. Исследование функций и построение графиков. Асимптоты графика функции Средняя линия треугольника
Средняя линия треугольника Логические задачки на умение ориентироваться в числовом ряду
Логические задачки на умение ориентироваться в числовом ряду Область определения функции
Область определения функции Пирамида
Пирамида РўР’РёРњРЎ_Лекция 4_Дискретные СЃРучайные РІРµРичины
РўР’РёРњРЎ_Лекция 4_Дискретные СЃРучайные РІРµРичины Игра в стручки
Игра в стручки Понятие вектора. Равенство векторов
Понятие вектора. Равенство векторов