Презентация на тему Средняя линия треугольника

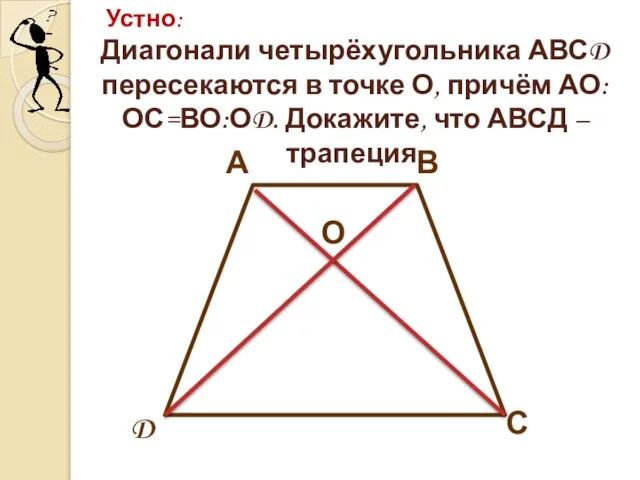
А
В
С
D
О
Диагонали четырёхугольника АВСD пересекаются в точке О, причём АО:ОС=ВО:ОD. Докажите, что АВСД –трапеция.
Устно:

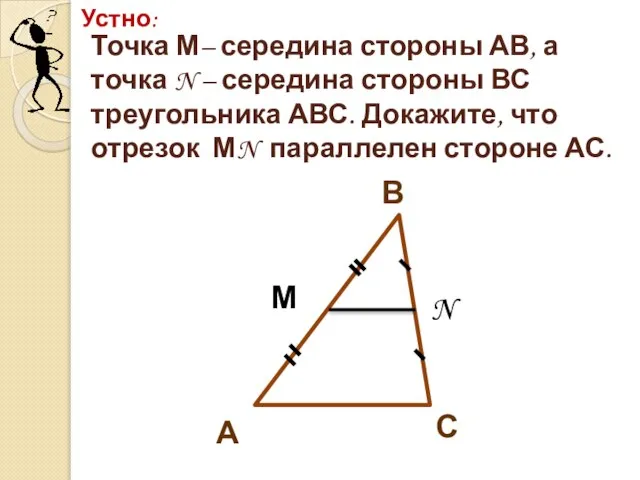
Устно:
С
В
А
М
N
Точка М– середина стороны АВ, а точка N – середина стороны ВС треугольника АВС. Докажите, что отрезок МN параллелен стороне АС.

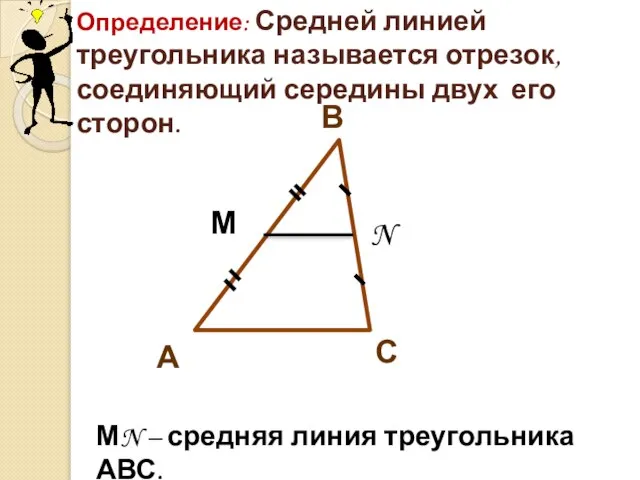
С
В
А
М
N
Определение: Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
МN – средняя линия треугольника АВС.

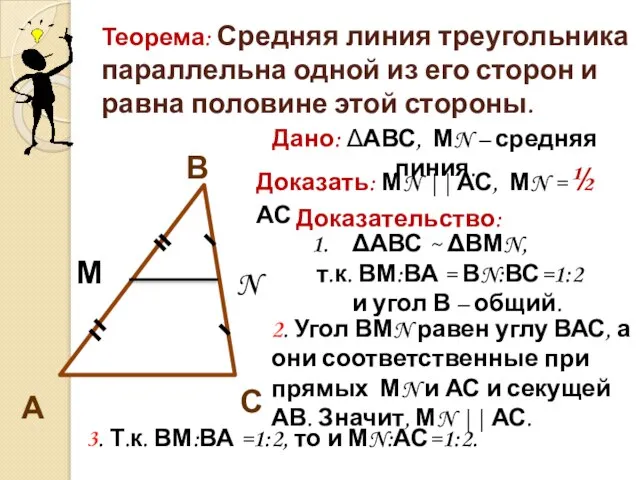
Теорема: Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
С
В
А
М
N
Дано: ΔАВС, МN – средняя линия.
Доказать: МN || АС, МN =½ АС
Доказательство:
ΔАВС ~ ΔВМN,
т.к. ВМ:ВА = ВN:ВС=1:2 и угол В – общий.
2. Угол ВМN равен углу ВАС, а они соответственные при прямых МN и АС и секущей АВ. Значит, МN || АС.
3. Т.к. ВМ:ВА =1:2, то и МN:АС=1:2.

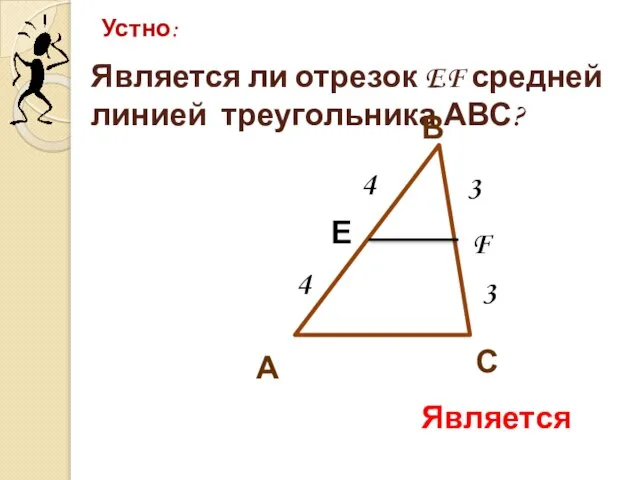
Является ли отрезок EF средней линией треугольника АВС?
Устно:
С
В
А
Е
F
3
3
4
4
Является

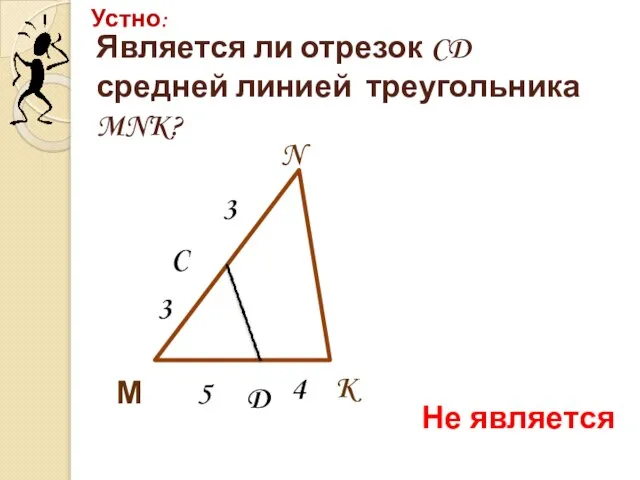
Является ли отрезок CD средней линией треугольника MNK?
Устно:
K
N
М
C
D
4
5
3
3
Не является

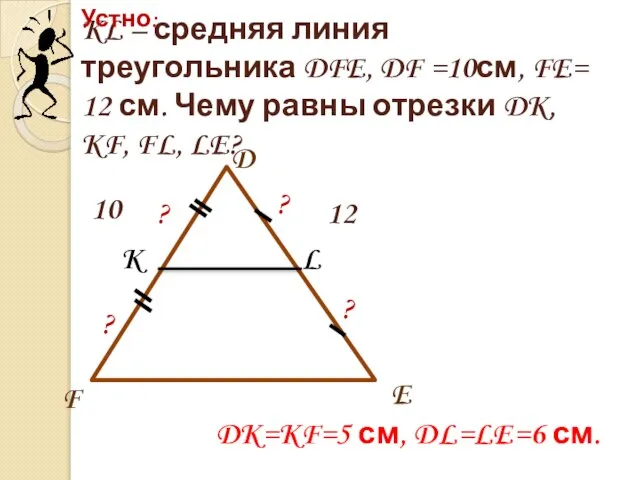
KL – средняя линия треугольника DFE, DF =10см, FE= 12 см. Чему равны отрезки DK, KF, FL, LE?
10
12
?
?
?
?
Устно:
E
D
F
K
L
?
DK=KF=5 см, DL=LE=6 см.

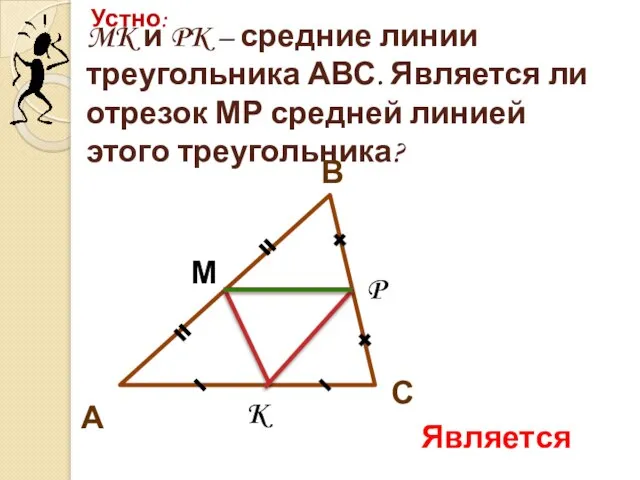
MK и PK – средние линии треугольника АВС. Является ли отрезок МР средней линией этого треугольника?
Устно:
С
В
А
М
P
K
Является

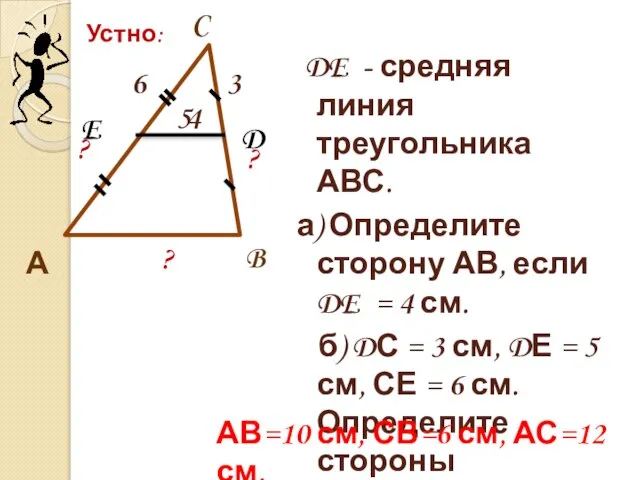
DE - средняя линия треугольника АВС.
а) Определите сторону АВ, если DE = 4 см.
б) DС = 3 см, DЕ = 5 см, СЕ = 6 см. Определите стороны треугольника АВС.
4
?
3
5
6
Устно:
B
C
А
E
D
?
?
АВ=10 см, СВ=6 см, АС=12 см.

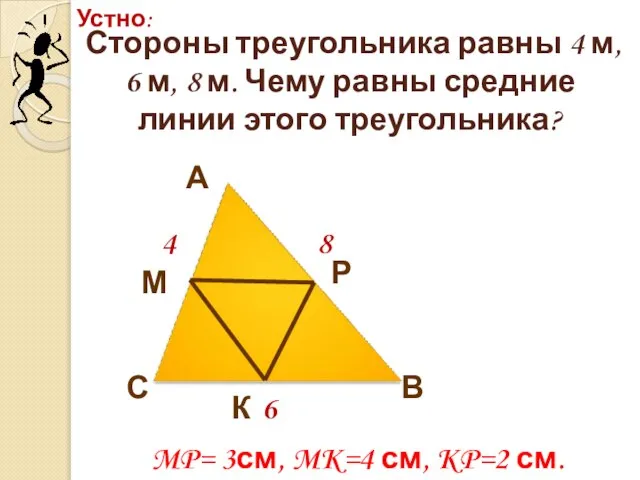
Стороны треугольника равны 4 м, 6 м, 8 м. Чему равны средние линии этого треугольника?
4
6
8
А
В
С
М
Р
К
Устно:
MP= 3см, MK=4 см, KP=2 см.

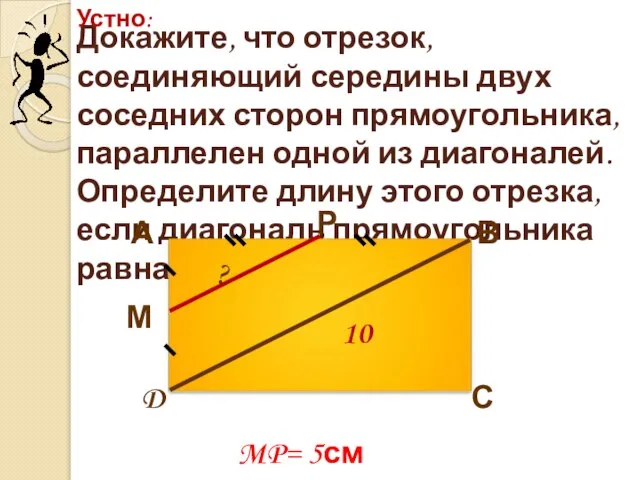
Докажите, что отрезок, соединяющий середины двух соседних сторон прямоугольника, параллелен одной из диагоналей. Определите длину этого отрезка, если диагональ прямоугольника равна 10 см.
А
В
С
D
М
Р
10
?
Устно:
MP= 5см

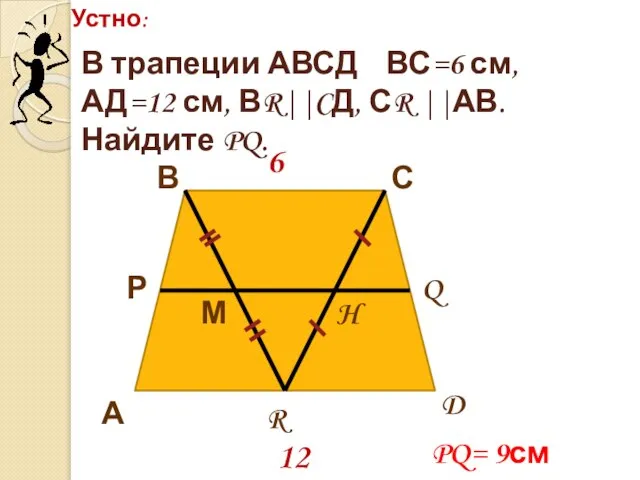
Устно:
А
В
С
D
Р
Q
М
H
R
6
12
В трапеции АВСД ВС=6 см, АД=12 см, ВR||CД, СR ||АВ. Найдите PQ.
PQ= 9см

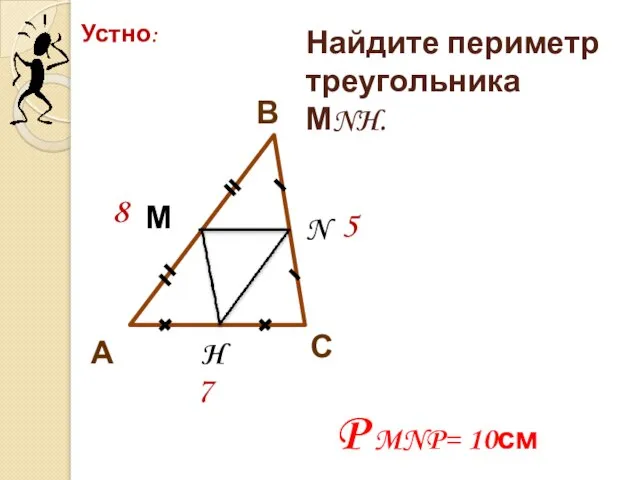
Устно:
С
В
А
М
N
H
8
5
7
Найдите периметр треугольника МNH.
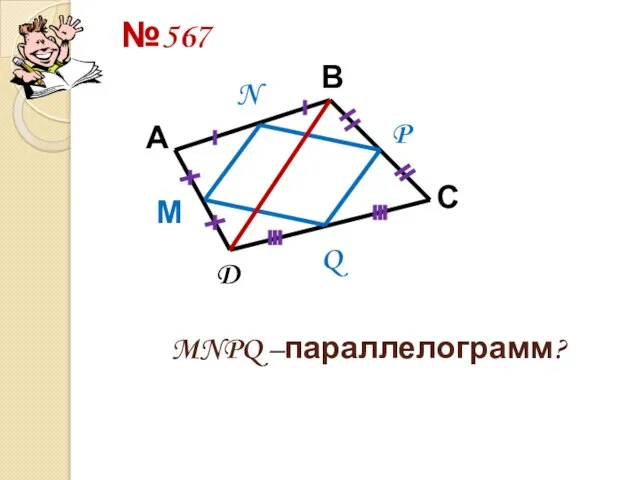
P MNP= 10см

№567
А
В
С
D
М
N
P
Q
MNPQ –параллелограмм?