Содержание
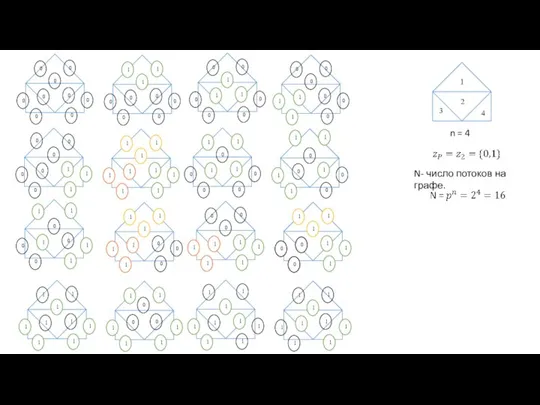
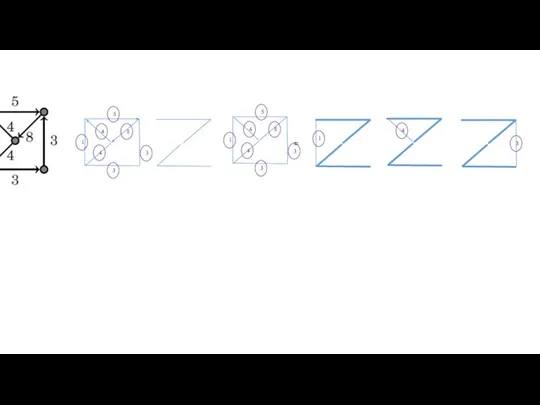
- 2. n = 4 N- число потоков на графе.
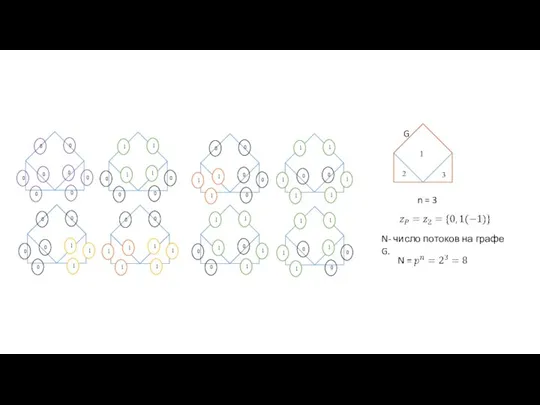
- 3. n = 3 N- число потоков на графе G. G
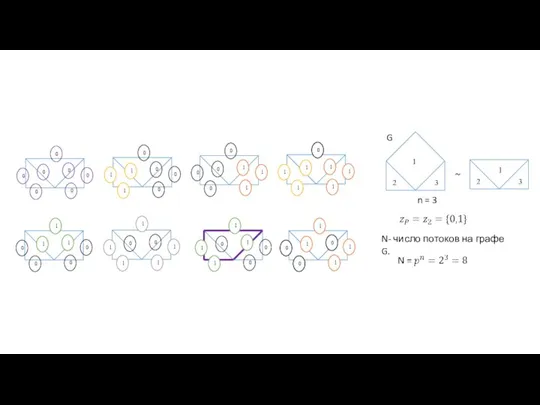
- 4. n = 3 N- число потоков на графе G. G ~
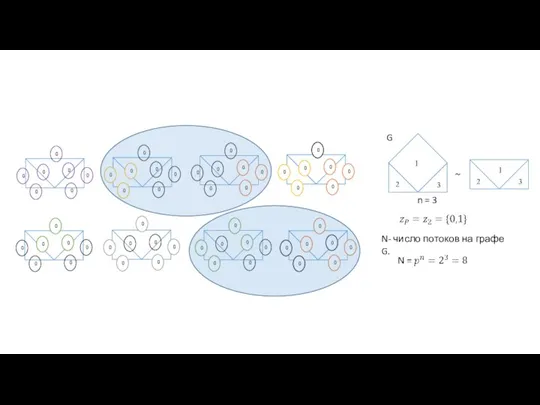
- 5. n = 3 N- число потоков на графе G. G ~
- 6. = 1 4 3
- 11. 1. На каком наименьшем количестве ребер графа G достаточно задать значение потока так, чтобы поток был
- 12. 13. Найдите все корни многочлена P(x) = x3 + x2 + 2, принадлежащие GL(3, F3) ,
- 13. 12. Найдите все корни многочлена x3 + x2 + 2, принадлежащие GL(3, F3). Продолжение: P(M)= M
- 14. 12. Найдите все корни многочлена x3 + x2 + 2•1, принадлежащие GL(3, F3). Продолжение: P(M)= M
- 15. 12. Найдите все корни многочлена x3 + x2 + 2•1, принадлежащие GL(3, F3). Продолжение: P(M)= M
- 16. 12. Найдите все корни многочлена x3 + x2 + 2•1, принадлежащие GL(3, F3). Продолжение: P(M)= M
- 17. 12. Найдите все корни многочлена x3 + x2 + 2, принадлежащие GL(3, F3). Продолжение: 4) Воспользуемся
- 18. Найдите все корни многочлена x2 + 3x+ 1, принадлежащие GL(2, F7).
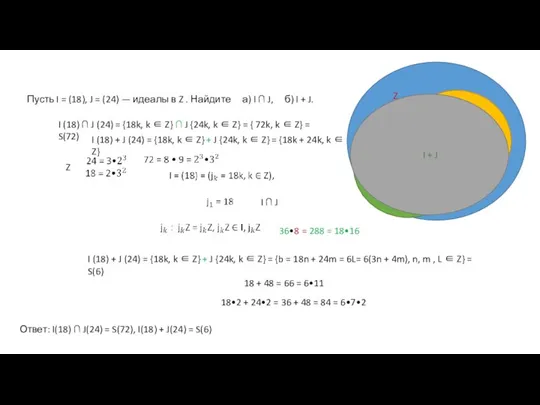
- 19. Пусть I = (18), J = (24) — идеалы в Z . Найдите а) I ∩
- 24. Скачать презентацию














 Формулы сложения
Формулы сложения Задачи на построение. 7 класс
Задачи на построение. 7 класс Математическое описание случайных явлений
Математическое описание случайных явлений Основные характеристики средств измерений. Лекция 4
Основные характеристики средств измерений. Лекция 4 Первообразная и неопределённый интеграл
Первообразная и неопределённый интеграл Площади фигур
Площади фигур Решение треугольников
Решение треугольников Вычисли и запомни
Вычисли и запомни Равнобедренный треугольник. Прямоугольник. Параллелограмм ,не являющийся прямоугольником. Равновеликие фигуры
Равнобедренный треугольник. Прямоугольник. Параллелограмм ,не являющийся прямоугольником. Равновеликие фигуры Некоторые свойства прямоугольных треугольников. Решение задач
Некоторые свойства прямоугольных треугольников. Решение задач Новые фигуры из квадратов и кругов
Новые фигуры из квадратов и кругов Чтение и запись многозначных чисел. Класс миллионов. Класс миллиардов
Чтение и запись многозначных чисел. Класс миллионов. Класс миллиардов Осевая симметрия
Осевая симметрия Формулы Крамера. Системы линейных алгебраических уравнений
Формулы Крамера. Системы линейных алгебраических уравнений Тема Функция у = ах2 и её график
Тема Функция у = ах2 и её график Квадратные уравнения
Квадратные уравнения Математичний квест. Дорогою до школи
Математичний квест. Дорогою до школи Путешествие по родному краю. Курильский заповедник. Выбери наибольшее число
Путешествие по родному краю. Курильский заповедник. Выбери наибольшее число Сумма углов в треугольнике
Сумма углов в треугольнике Формула стоимости. Формула пути
Формула стоимости. Формула пути Геометрия. Построение сечений
Геометрия. Построение сечений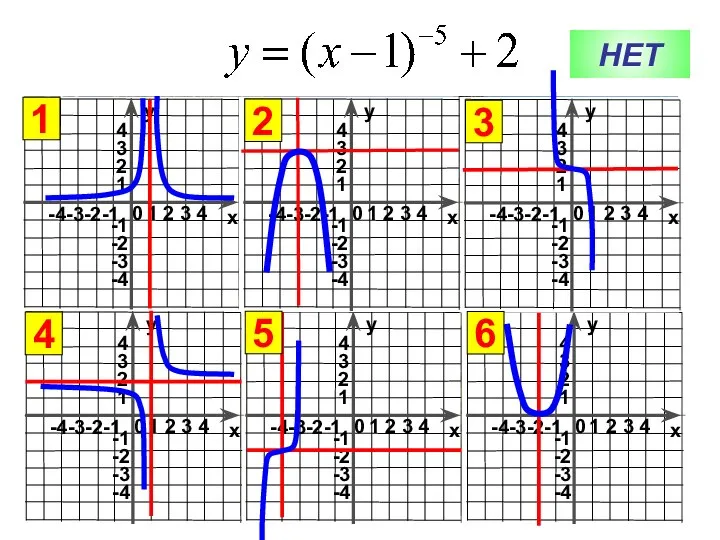 графики функций. Ошибка
графики функций. Ошибка Построение графика квадратичной функции
Построение графика квадратичной функции Треугольник. Контрольная работа по геометрии
Треугольник. Контрольная работа по геометрии Смежные и вертикальные углы
Смежные и вертикальные углы Особенности проведения олимпиады по математике в 2016-17 учебном году
Особенности проведения олимпиады по математике в 2016-17 учебном году Презентация по математике "Мы рады привествовать вас на уроке математики" -
Презентация по математике "Мы рады привествовать вас на уроке математики" -  Решаем задачи. Составляем обратные задачи (Урок 19)
Решаем задачи. Составляем обратные задачи (Урок 19)