Содержание
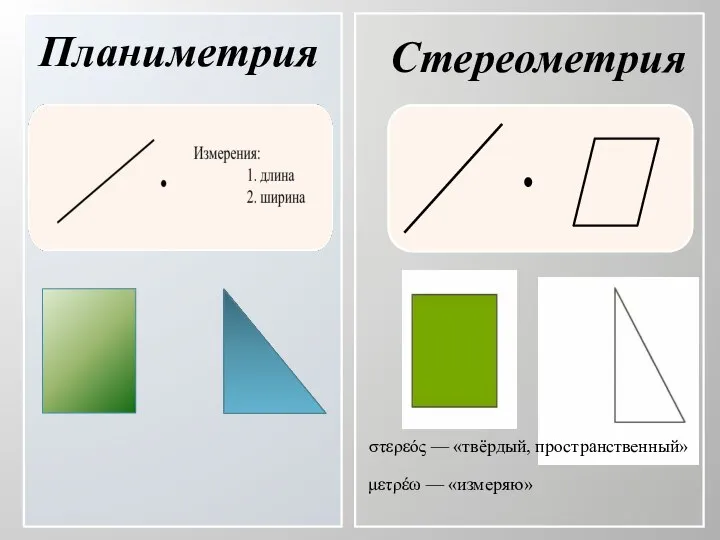
- 2. Планиметрия Стереометрия στερεός — «твёрдый, пространственный» μετρέω — «измеряю»
- 3. Стереометрия
- 4. Измерения: Длина. Ширина. Высота. Геометрическое тело обладает вместимостью
- 5. Геометрические тела, как и все геометрические фигуры, являются воображаемыми объектами. Геометрическое тело – часть пространства, отделенное
- 9. Пифагорейская философская школа VI – V вв. до нашей эры Пифагор Самосский 570 — 490 гг.
- 11. Некоторые следствия из аксиом стереометрии
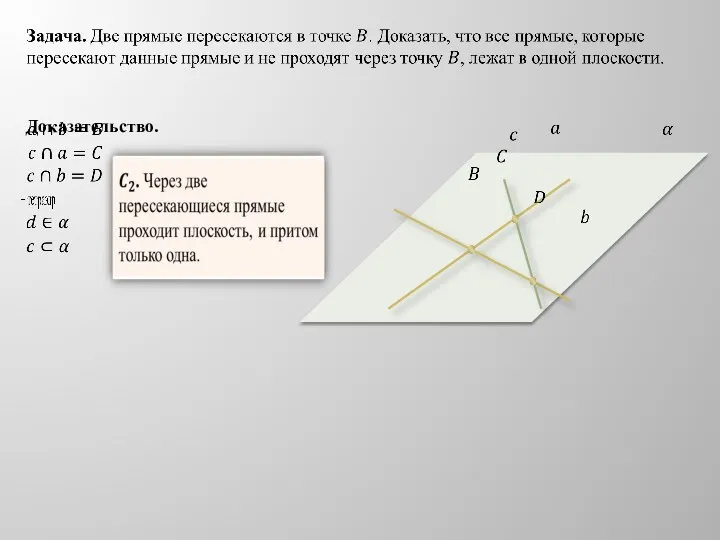
- 12. Доказательство.
- 13. Доказательство.
- 14. СПОСОБЫ ЗАДАНИЯ ПЛОСКОСТИ Через три точки не лежащие на одной прямой. Через прямую и не лежащую
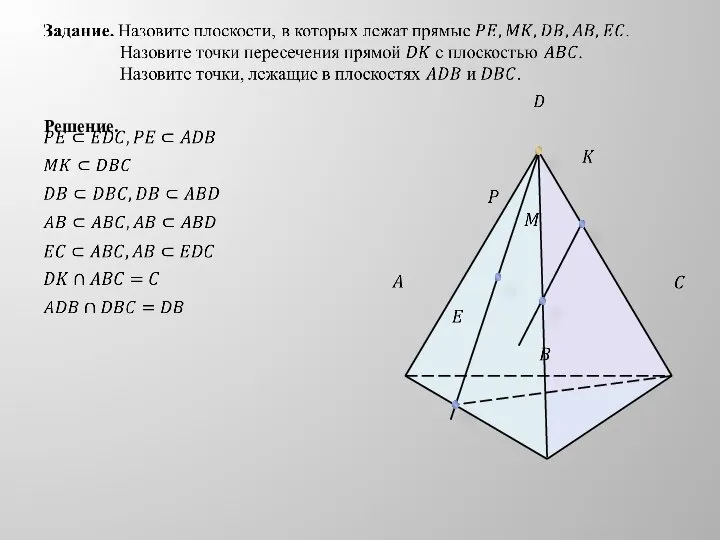
- 15. Решение.
- 16. Доказательство.
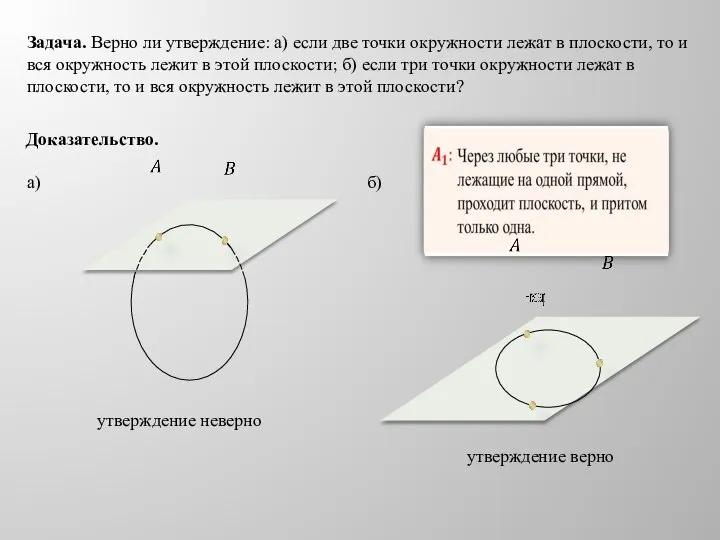
- 17. Задача. Верно ли утверждение: а) если две точки окружности лежат в плоскости, то и вся окружность
- 19. Скачать презентацию










 Изучение основ Анализа формальных понятий
Изучение основ Анализа формальных понятий Коэффициенты линейной функции
Коэффициенты линейной функции Решение простейших тригонометрических уравнений
Решение простейших тригонометрических уравнений Начальный замер. Цифры
Начальный замер. Цифры Теорема косинусов
Теорема косинусов Центральные и вписанные углы
Центральные и вписанные углы История арабских чисел
История арабских чисел Одночлены
Одночлены Найдите производную функции. Практическая работа
Найдите производную функции. Практическая работа Функциональная грамотность (математика) - задачи
Функциональная грамотность (математика) - задачи Четырехугольники. 2 урок
Четырехугольники. 2 урок Выбор схемы измерения переменных
Выбор схемы измерения переменных Интегрирование методом замены переменной
Интегрирование методом замены переменной Worksheet 3 (reatke)
Worksheet 3 (reatke) Задача линейного программирования. Канонический вид задачи линейного программирования
Задача линейного программирования. Канонический вид задачи линейного программирования Современное школьное математическое образование
Современное школьное математическое образование Сложение вида +2, +3
Сложение вида +2, +3 Расстояния и углы
Расстояния и углы Радианная мера угла
Радианная мера угла Тригонометрические тождества
Тригонометрические тождества Шарады, метаграммы, логогрифы
Шарады, метаграммы, логогрифы Знакомство с мерами длины
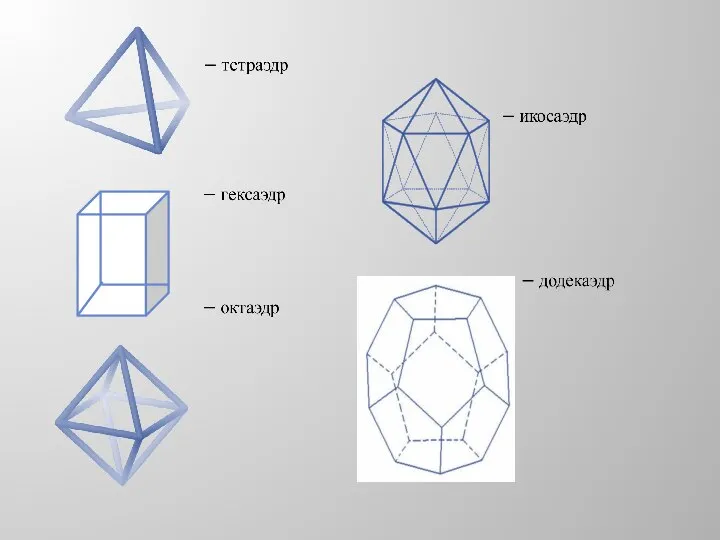
Знакомство с мерами длины Правильные многогранники. Моделирование многогранников
Правильные многогранники. Моделирование многогранников Метод обратной матрицы решения систем линейных уравнений
Метод обратной матрицы решения систем линейных уравнений Статистическая проверка статистических гипотез
Статистическая проверка статистических гипотез Презентация на тему Упрощение выражений 5 класс
Презентация на тему Упрощение выражений 5 класс  Знакомство с подсчётом вероятности
Знакомство с подсчётом вероятности Математическая модель
Математическая модель