Презентация на тему Тетраэдр (10 класс)

Сегодня мы познакомимся с ТЕТРАЭДРОМ.
Прежде чем ввести понятие тетраэдра, вспомним, что мы понимали под многоугольником в планиметрии.

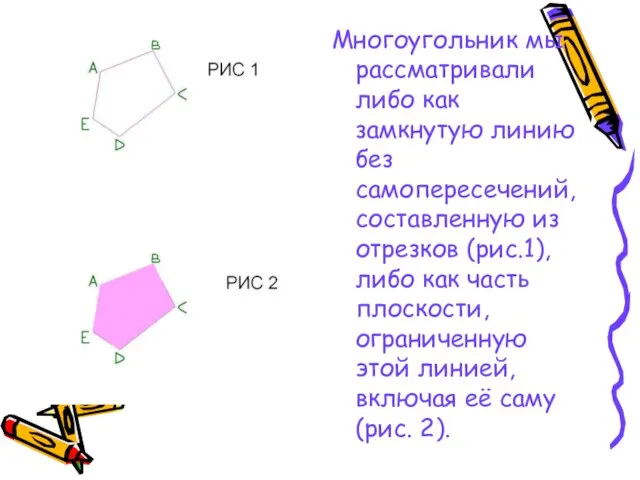
Многоугольник мы рассматривали либо как замкнутую линию без самопересечений, составленную из отрезков (рис.1), либо как часть плоскости, ограниченную этой линией, включая её саму(рис. 2).

ПЕРЕЙДЕМ ТЕПЕРЬ К ОПРЕДЕЛЕНИЮ ТЕТРАЭДРА

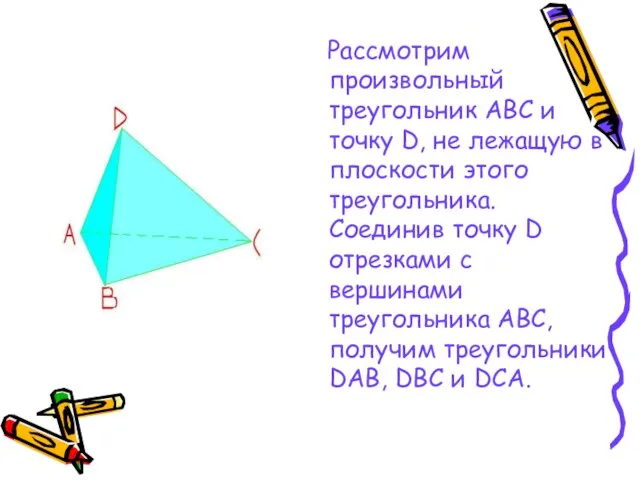
Рассмотрим произвольный треугольник АВС и точку D, не лежащую в плоскости этого треугольника. Соединив точку D отрезками с вершинами треугольника АВС, получим треугольники DAB, DBC и DCA.

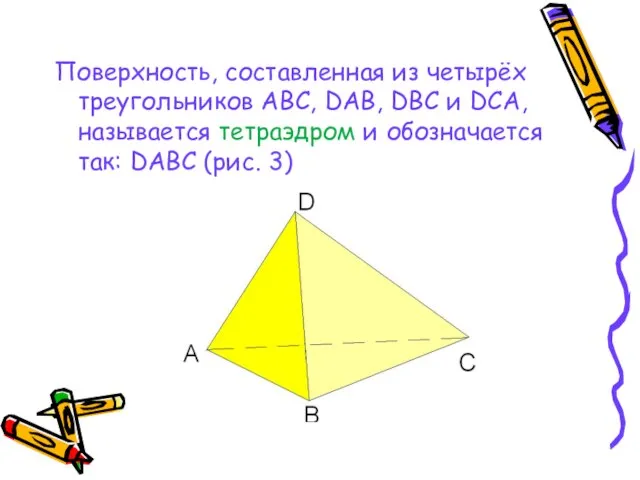
Поверхность, составленная из четырёх треугольников АВС, DAB, DBC и DCA, называется тетраэдром и обозначается так: DАBC (рис. 3)

Треугольники, из которых состоит тетраэдр, называются гранями, их стороны – ребрами, а вершины- вершинами тетраэдра. Тетраэдр имеет четыре грани, шесть ребер и четыре вершины. Иногда выделяют одну из граней тетраэдра и называют её основанием, а три другие – боковыми гранями.

Тетраэдр изображается в виде выпуклого или невыпуклого четырёхугольника с диагоналями. При этом штриховыми линиями изображаются невидимые рёбра.