Содержание
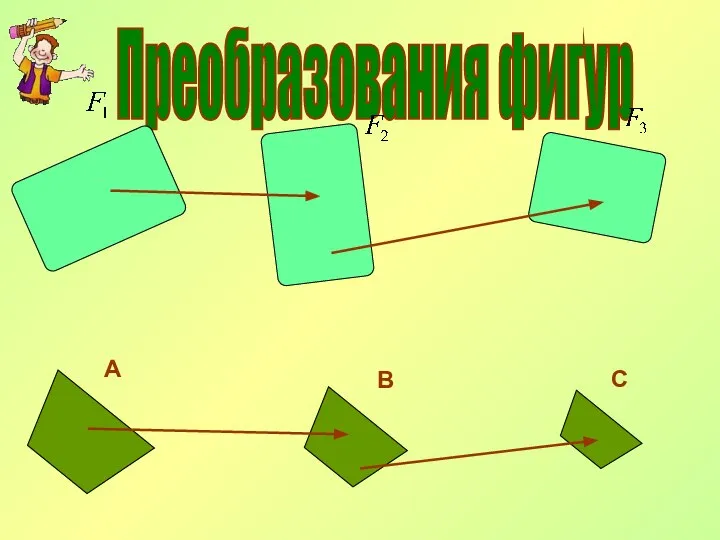
- 2. Преобразования фигур А В С
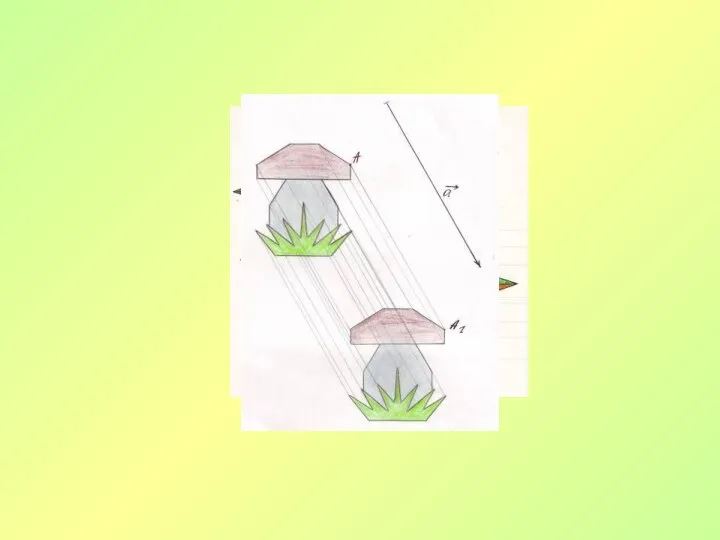
- 3. Движение Преобразование одной фигуры в другую, при котором сохраняется расстояние между точками называется движением.
- 4. .А .А
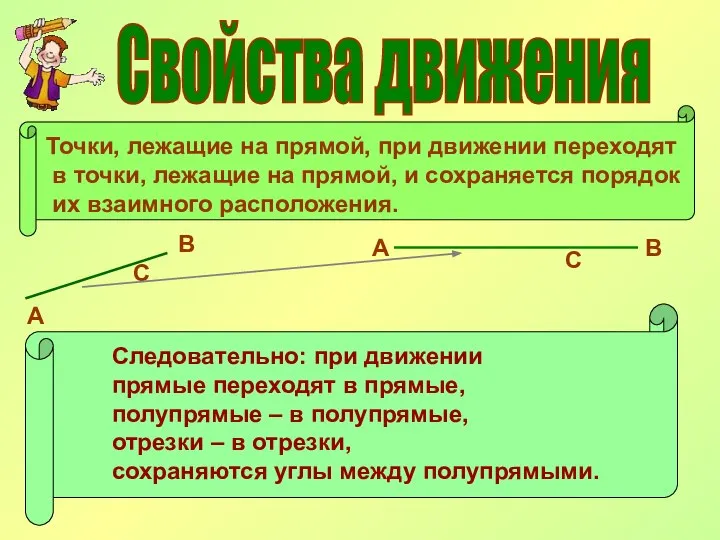
- 5. Свойства движения Точки, лежащие на прямой, при движении переходят в точки, лежащие на прямой, и сохраняется
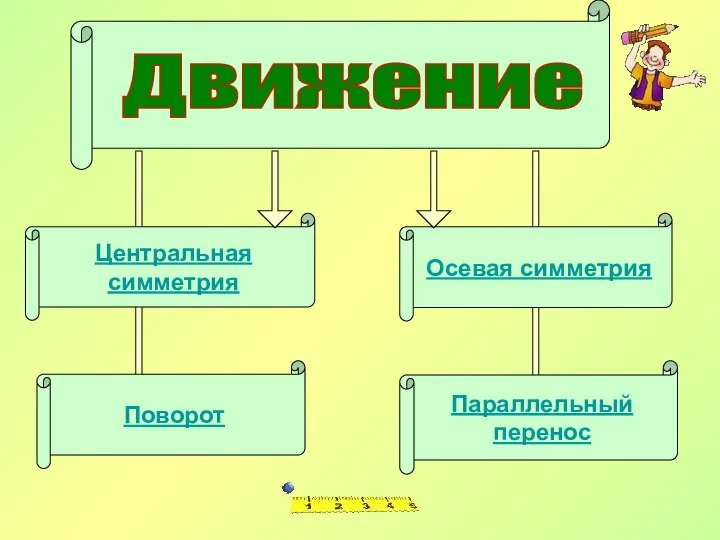
- 6. Движение Центральная симметрия Поворот Осевая симметрия Параллельный перенос
- 7. Решение задач: №1; 2 стр.126
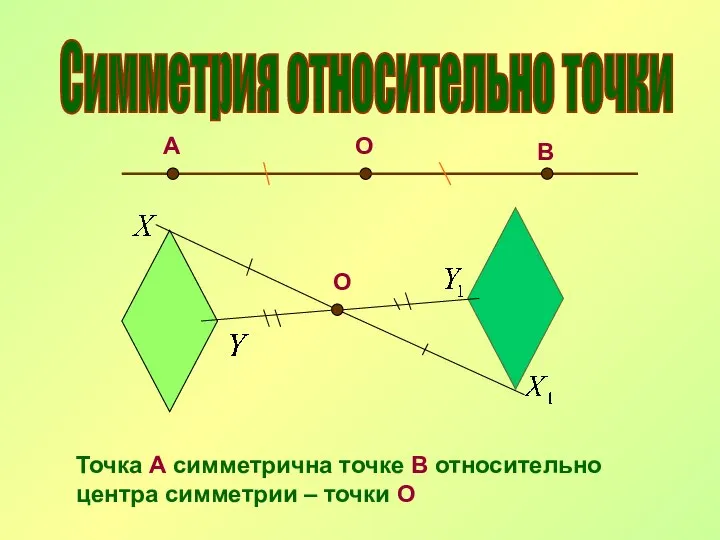
- 8. Симметрия относительно точки О А В О Точка А симметрична точке В относительно центра симметрии –
- 10. Решение задач: №3; 5 уст.; 7 уст.; 11-построить. Д/з: п.82-84; №6; 8; 10
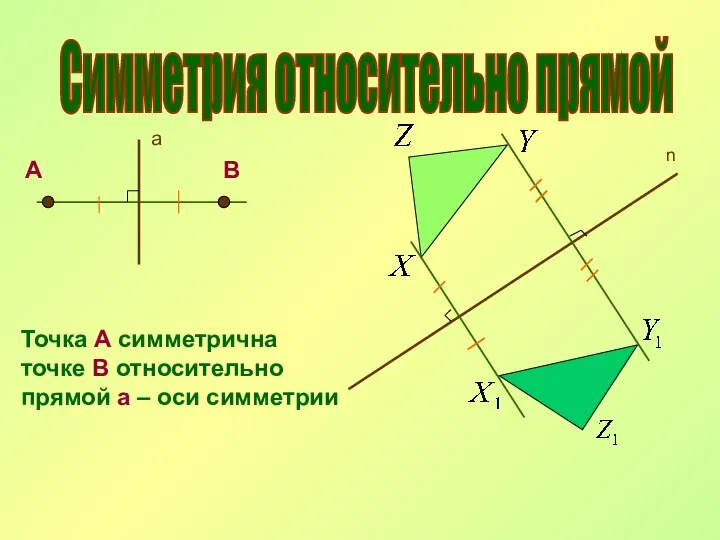
- 11. Симметрия относительно прямой а А В Точка А симметрична точке В относительно прямой а – оси
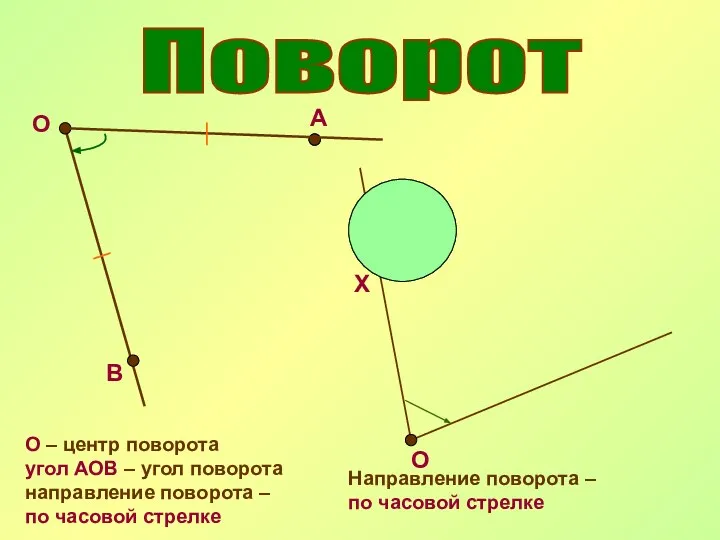
- 13. Поворот О А В О – центр поворота угол АОВ – угол поворота направление поворота –
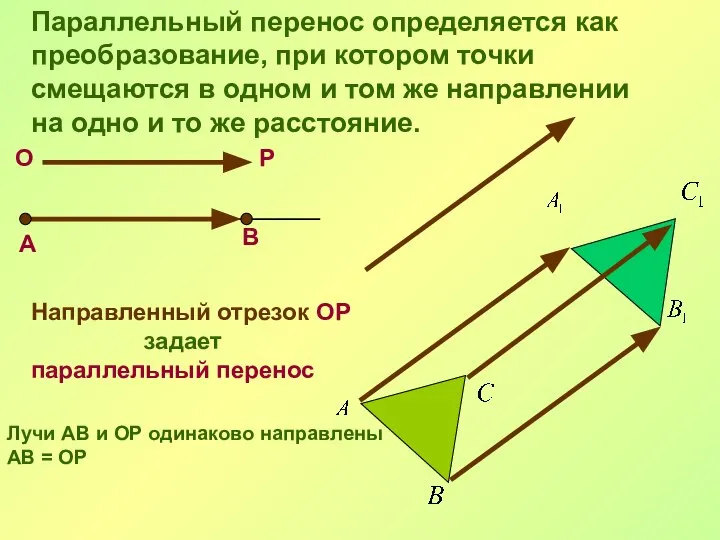
- 15. Параллельный перенос Преобразование фигуры F, при котором ее произвольная точка (х; у) переходит в точку (х+а;
- 16. В О Р А Направленный отрезок ОР задает параллельный перенос Лучи АВ и ОР одинаково направлены
- 18. Композиция движений
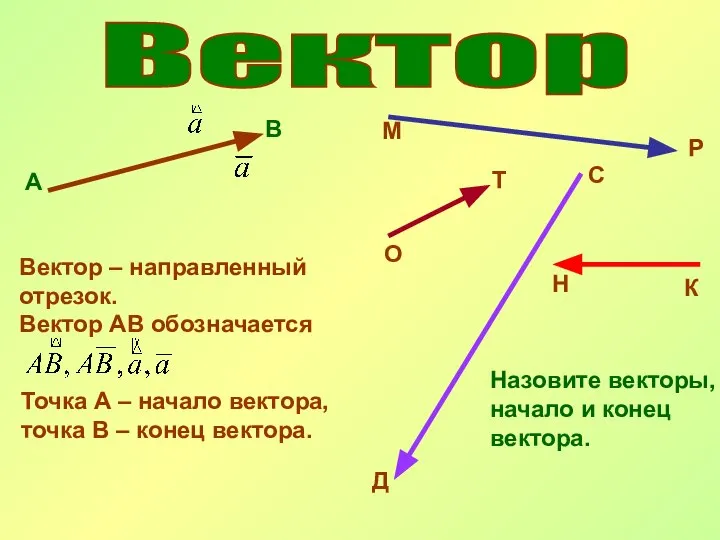
- 19. Вектор А В Вектор – направленный отрезок. Вектор АВ обозначается Точка А – начало вектора, точка
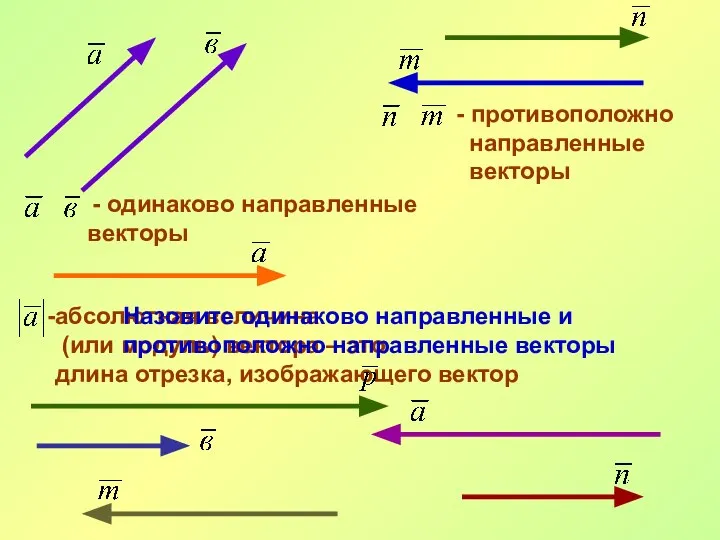
- 20. - одинаково направленные векторы - противоположно направленные векторы абсолютная величина (или модуль) вектора – это длина
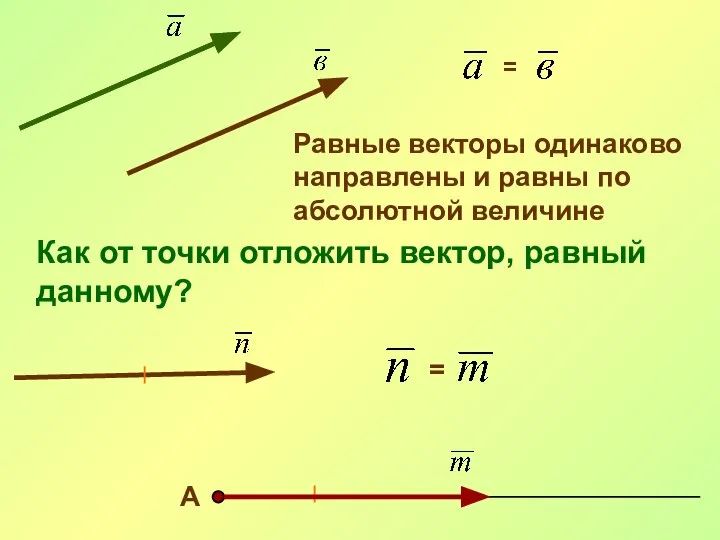
- 21. = Равные векторы одинаково направлены и равны по абсолютной величине Как от точки отложить вектор, равный
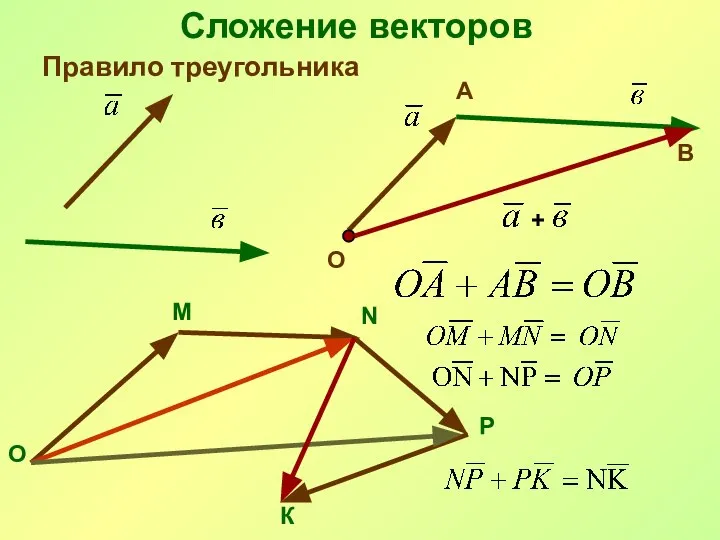
- 22. Сложение векторов Правило треугольника + О А В О М N Р К
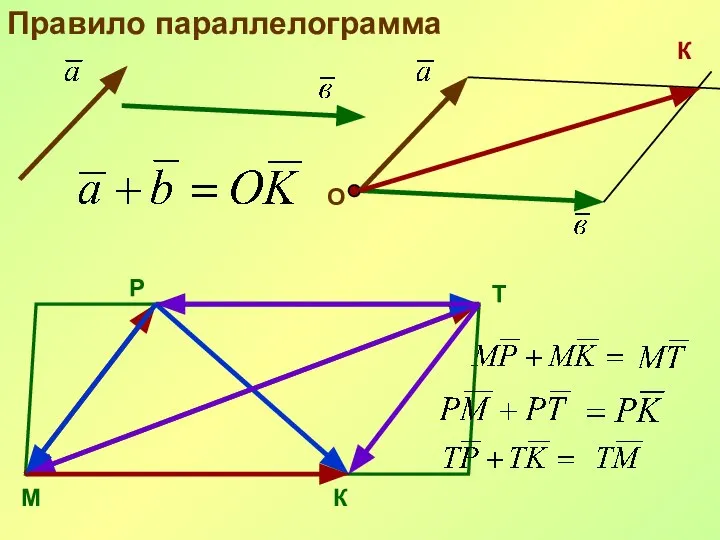
- 23. Правило параллелограмма О К М Р Т К
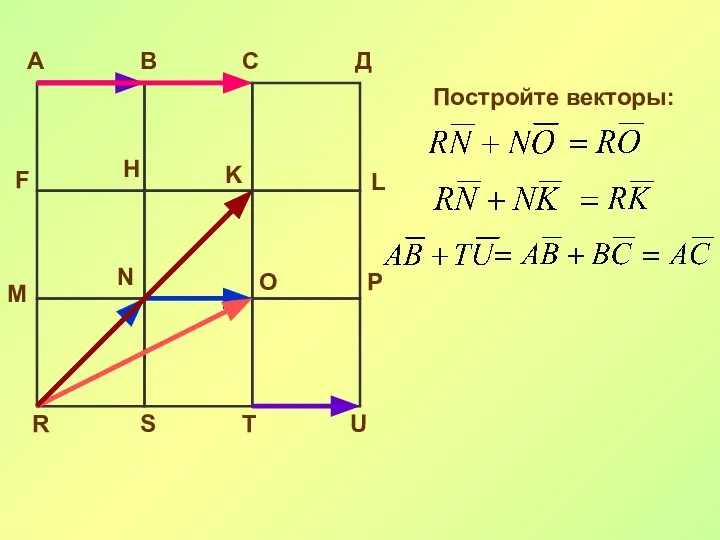
- 24. А В С Д F H K L M N O P R S T U
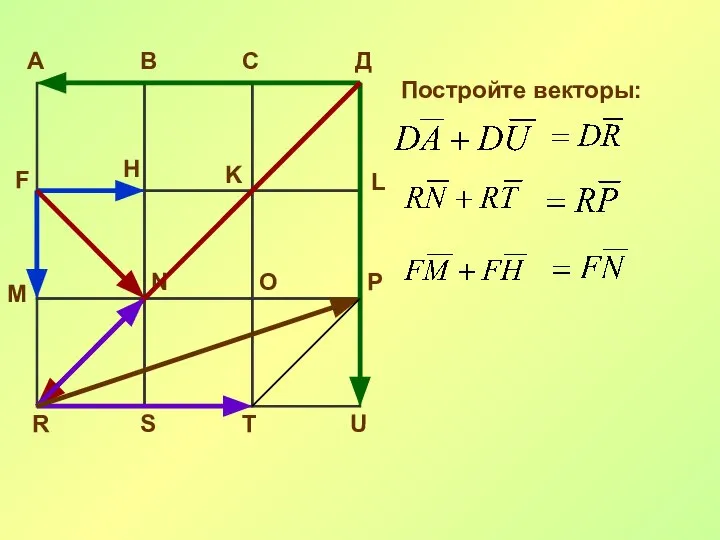
- 25. А В С Д F H K L M N O P R S T U
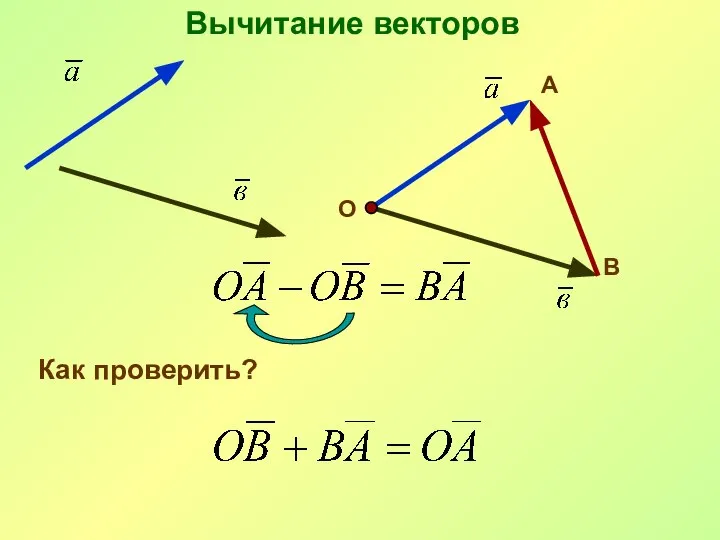
- 26. Вычитание векторов О А В Как проверить?
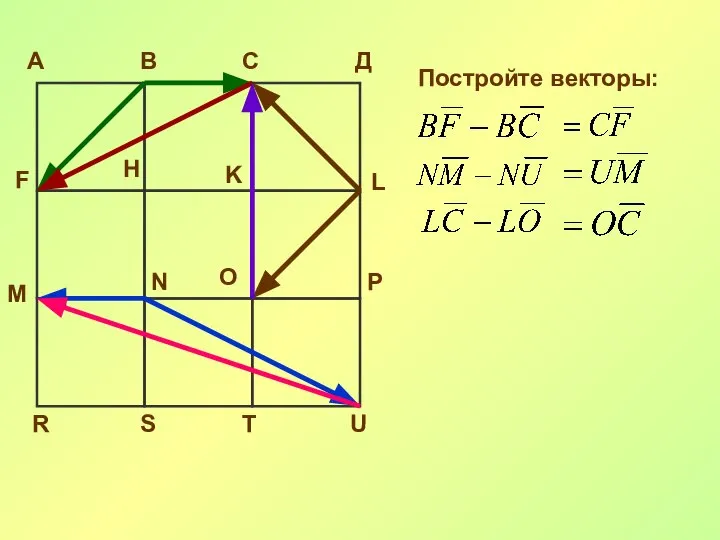
- 27. А В С Д F H K L M N O P R S T U
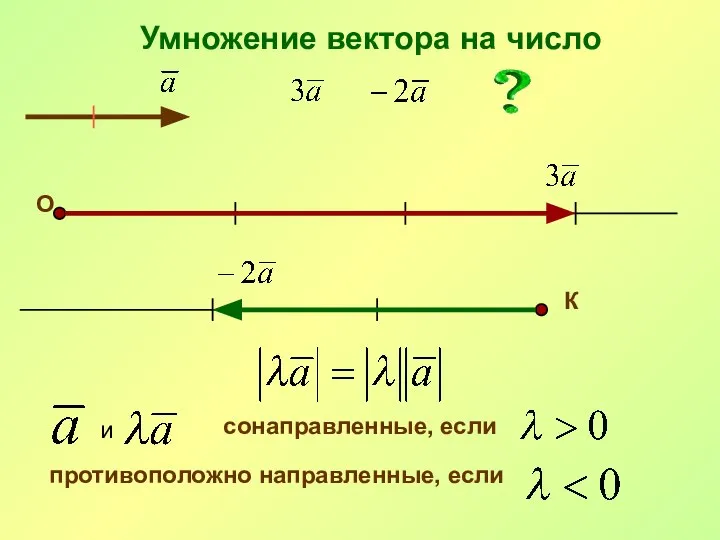
- 28. Умножение вектора на число О К и сонаправленные, если противоположно направленные, если
- 30. Скачать презентацию








 Методы оптимизации. Ограничения в виде равенств и неравенств
Методы оптимизации. Ограничения в виде равенств и неравенств Измерение углов
Измерение углов Тела и поверхности вращения
Тела и поверхности вращения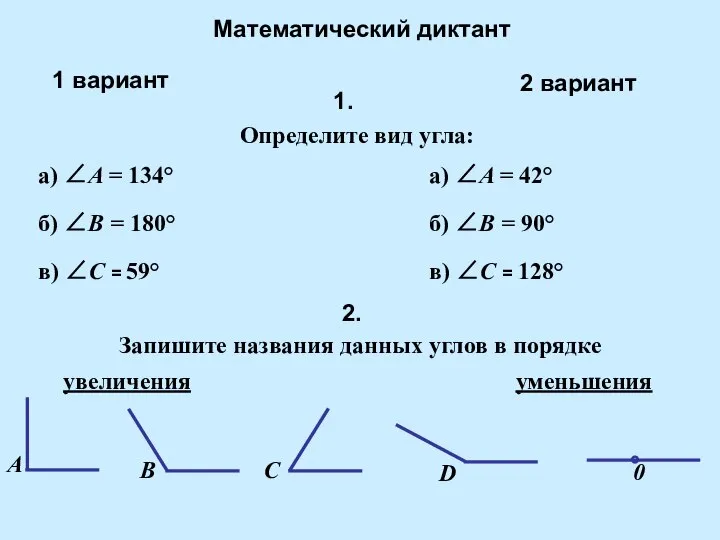 Математический диктант
Математический диктант Наибольшие и найменьшее значение функции
Наибольшие и найменьшее значение функции Первообразная. Интеграл
Первообразная. Интеграл Сложение с переходом через десяток
Сложение с переходом через десяток Критерии оценивания 22 задания (демонстрационный вариант 2022 года)
Критерии оценивания 22 задания (демонстрационный вариант 2022 года) Процент от числа
Процент от числа Знакочередующиеся и знакопеременные ряды
Знакочередующиеся и знакопеременные ряды Составление примеров на сложение
Составление примеров на сложение Порядок действий
Порядок действий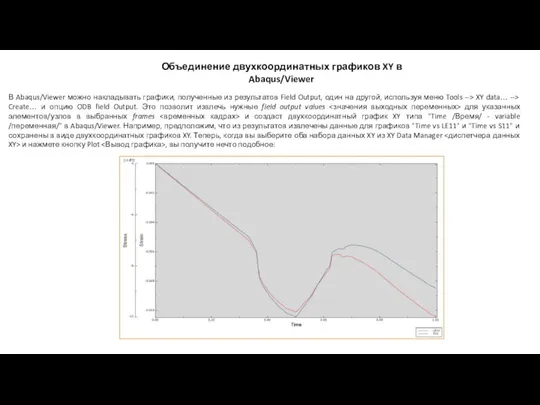 Объединение двухкоординатных графиков XY в Abaqus/Viewer
Объединение двухкоординатных графиков XY в Abaqus/Viewer 07.09.22 Огляд елементарних функцій (1)
07.09.22 Огляд елементарних функцій (1) Лист Мебиуса
Лист Мебиуса ВПР по математике. Тренировочные задания
ВПР по математике. Тренировочные задания Производные высших порядков
Производные высших порядков Параллельные прямые
Параллельные прямые Введение в комбинаторику. 7 класс
Введение в комбинаторику. 7 класс Генеральная средняя
Генеральная средняя Сфера описанная или вписанная
Сфера описанная или вписанная Цифры в пословицах
Цифры в пословицах Векторное и смешанное произведения векторов
Векторное и смешанное произведения векторов Преобразование выражений, содержащих квадратные корни
Преобразование выражений, содержащих квадратные корни Математический диктант
Математический диктант Теория вероятностей
Теория вероятностей Элементы теории фредгольмовых отображений
Элементы теории фредгольмовых отображений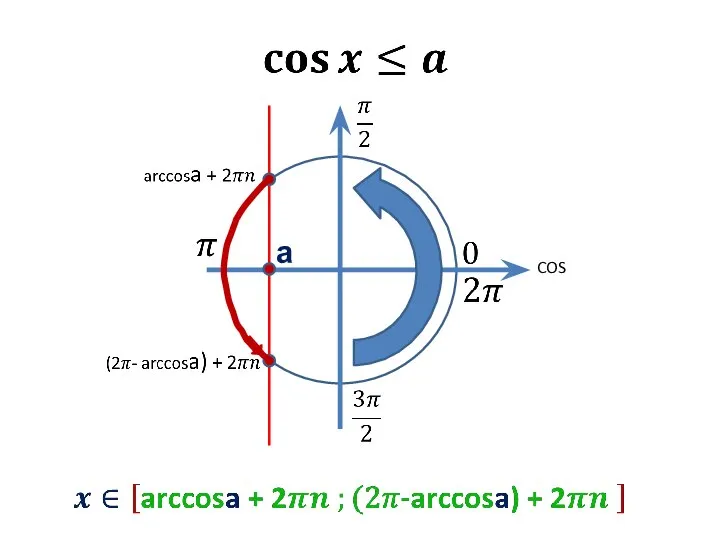 Неравенства вида Cos〖x≤a〗
Неравенства вида Cos〖x≤a〗