ug_skal

Цели урока:
Ввести понятия угла между
векторами и скалярного
произведения векторов.
Рассмотреть формулу
скалярного произведения в координатах.
Показать применение скалярного произведения векторов при решении задач.

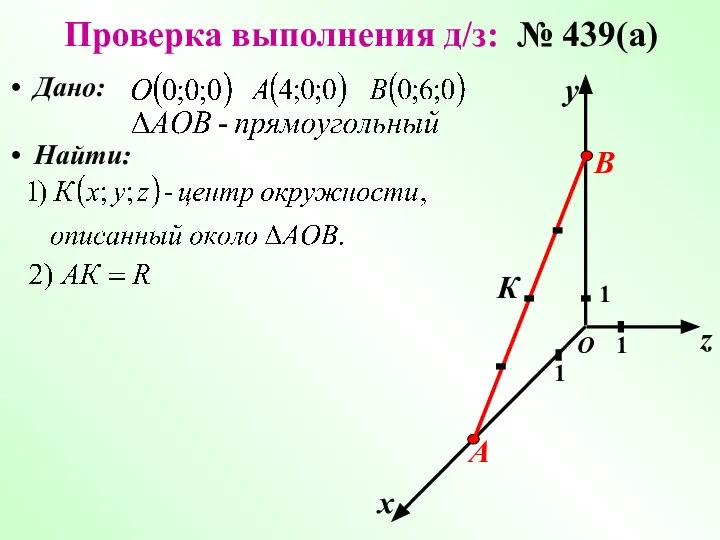
Проверка выполнения д/з: № 439(а)
Дано:
х
у
z
1
1
1
О
Найти:
А
В
К

Проверка выполнения д/з: № 439(а)
х
у
z
1
1
1
О
Решение:
А
В
К
Центр окружности К – середина
гипотенузы АВ. Найдем координаты К.
К (2; 3; 0)
Ответ:

Повторение:
Какие векторы называются равными?
Как найти длину вектора по координатам его начала и конца?
А
В
Какие векторы называются коллинеарными?
или

Повторение. (Устно)
Векторы в пространстве.
1) Дано:
Найти:
2) Дано:
Равны ли векторы и ?
Нет, т.к.равные векторы имеют равные
координаты.
3) Дано:
? Коллинеарны ли векторы и ?
Нет

Угол между векторами.
О
А
В
α
Если то
Если то
Если то

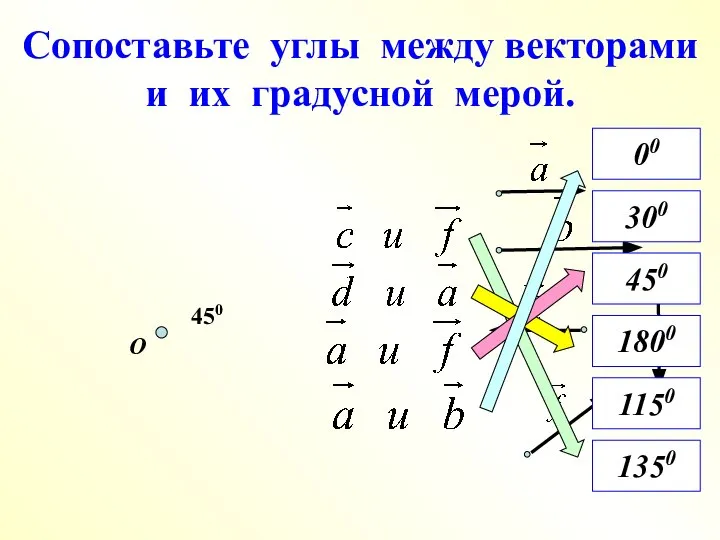
Сопоставьте углы между векторами и их градусной мерой.
О
450
1350
450
1800
00
300
1150

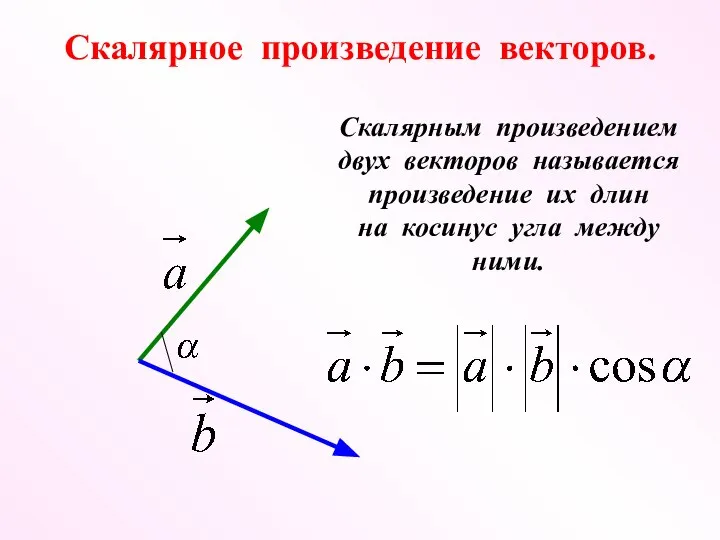
Скалярное произведение векторов.
Скалярным произведением
двух векторов называется
произведение их длин
на косинус угла между
ними.

Скаляр – лат. scale – шкала.
Ввел в 1845 г.
У. ГАМИЛЬТОН, английский математик.

Если , то
Если
, то
Если
, то
Если
, то
Скалярное произведение
называется
скалярным квадратом вектора
Вспомним планиметрию…

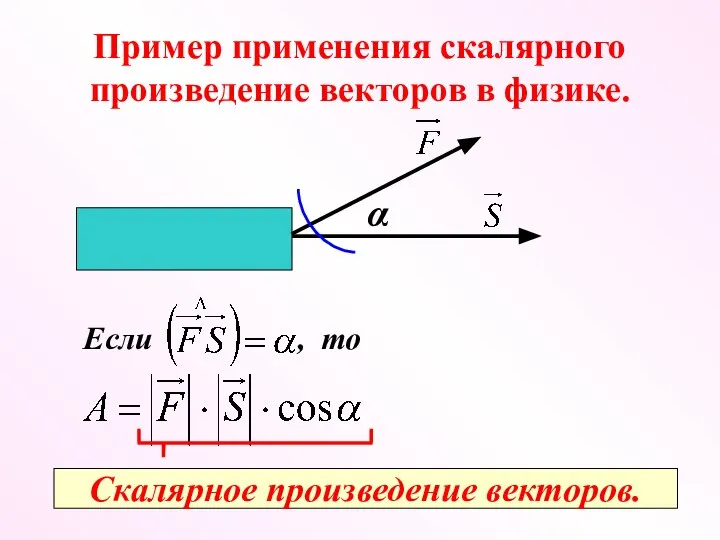
Пример применения скалярного произведение векторов в физике.
α
Если , то
Скалярное произведение векторов.

Формула скалярного произведения векторов в пространстве.
Скалярное произведение двух векторов равно сумме произведений соответствующих координат этих векторов.

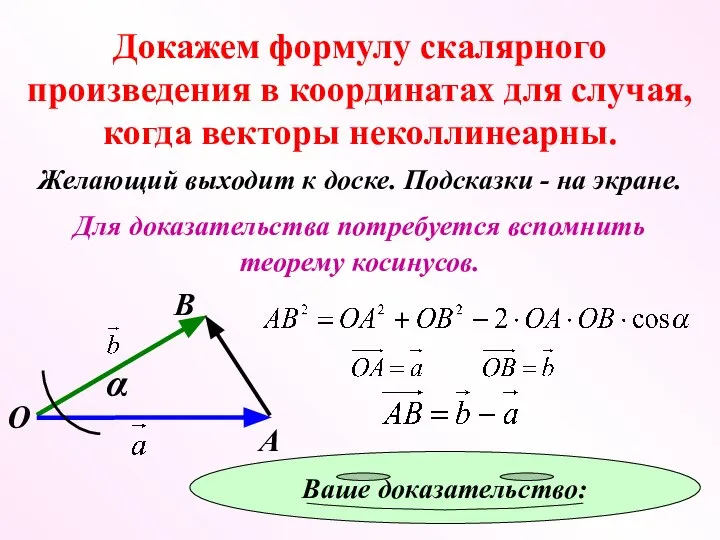
Докажем формулу скалярного произведения в координатах для случая, когда векторы неколлинеарны.
Желающий выходит к доске. Подсказки - на экране.
Для доказательства потребуется вспомнить
теорему косинусов.
А
В
О
α
Ваше доказательство:

Дома, следуя рекомендациям в учебнике, вывести формулу cos α
для двух ненулевых векторов в пространстве, зная их координаты.
«Геометрия 10-11», глава V, § 2, п.47.
№№ 141 (в – з); 443 (д; е)
+

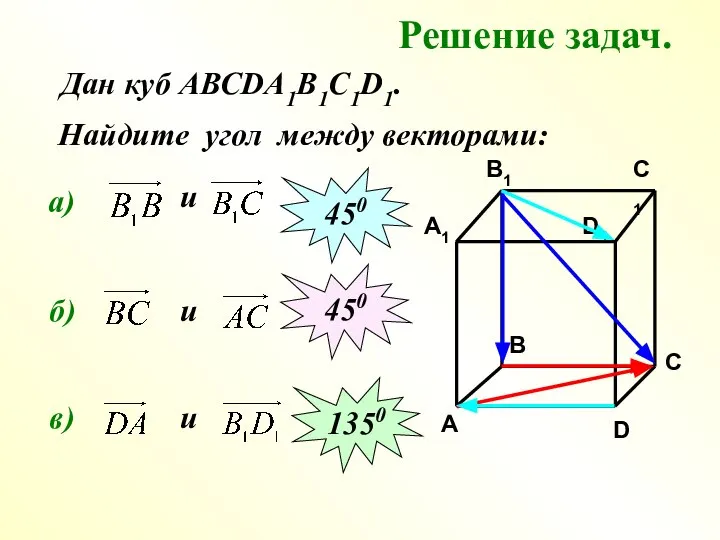
Решение задач.
Найдите угол между векторами:
а)
и
450
б)
и
450
в)
Дан куб АВСDA1B1C1D1.
и
1350

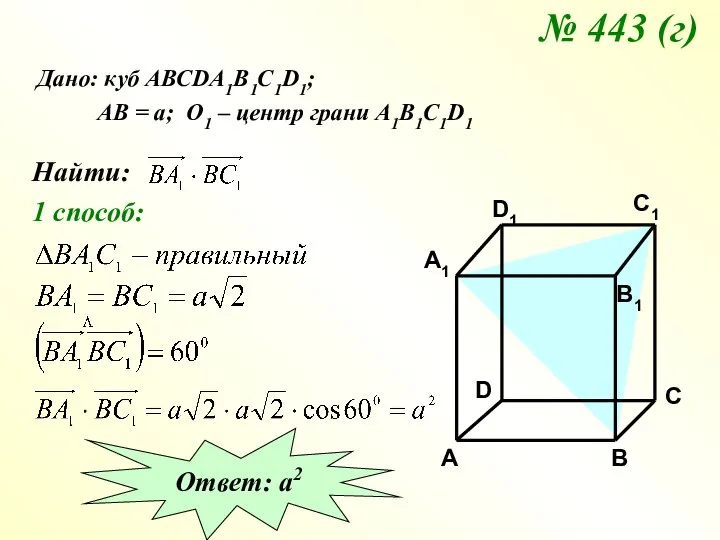
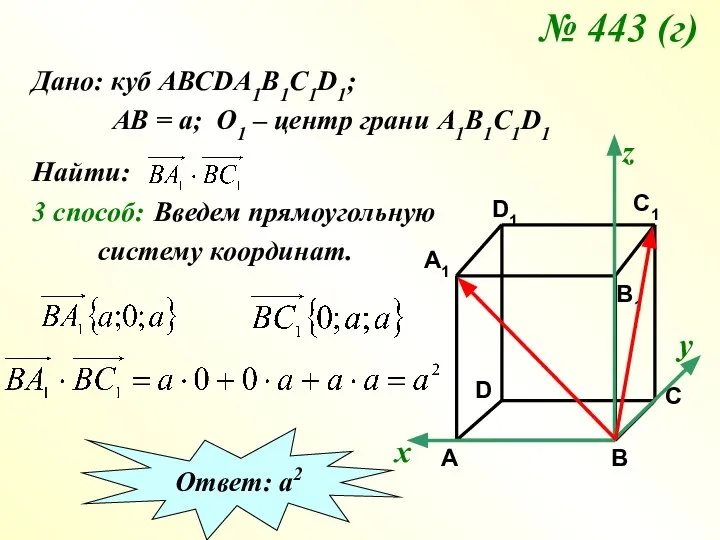
№ 443 (г)
Дано: куб АВСDA1B1C1D1;
АВ = а; О1 – центр грани А1В1С1D1
Найти:
1 способ:
Ответ: а2

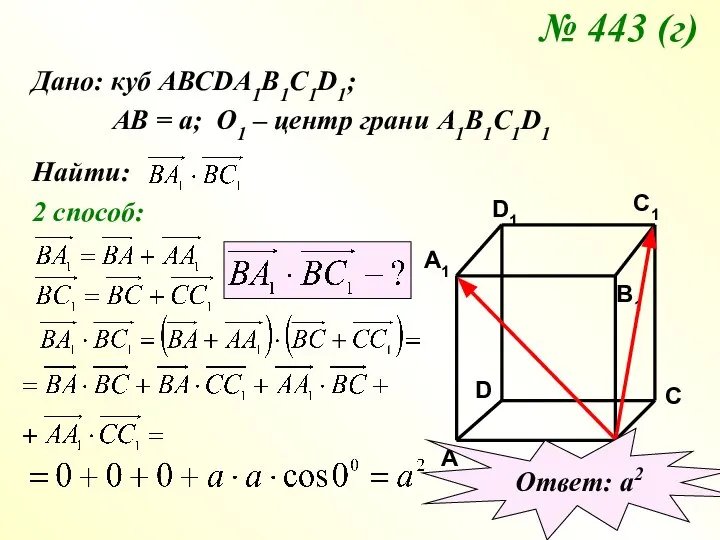
№ 443 (г)
Дано: куб АВСDA1B1C1D1;
АВ = а; О1 – центр грани А1В1С1D1
Найти:
2 способ:
Ответ: а2

№ 443 (г)
Дано: куб АВСDA1B1C1D1;
АВ = а; О1 – центр грани А1В1С1D1
Найти:
3 способ:
Введем прямоугольную
систему координат.
х
у
z
Ответ: а2

№ 443
Решаем по группам:
1 – а)
2 – б)
3 – в)
а2
-2а2
0
Дополнительная задача:
Вычислите угол между вектором а и координатным вектором i.