Содержание
- 2. Для чего нужны синусы и косинусы в обычной жизни? На практике синусы и косинусы применяются во
- 4. Детская школа Гауди в Барселоне
- 5. Ресторан в Лос-Манантиалесе в Аргентине
- 6. Мост в Сингапуре
- 10. Немного из истории… 1. Древние вавилоняне и египтяне изучали тригонометрию как часть астрономии; разделили окружность на
- 11. Немного из истории… 4. Насир ад-Дин Мухаммад ат-Туси (1201-1274) выделил раздел тригонометрии из астрономии. 5. Лев
- 12. Тригонометрия раздел математики, изучающий соотношение сторон и углов в треугольнике («три» - три, «гониа» - угол,
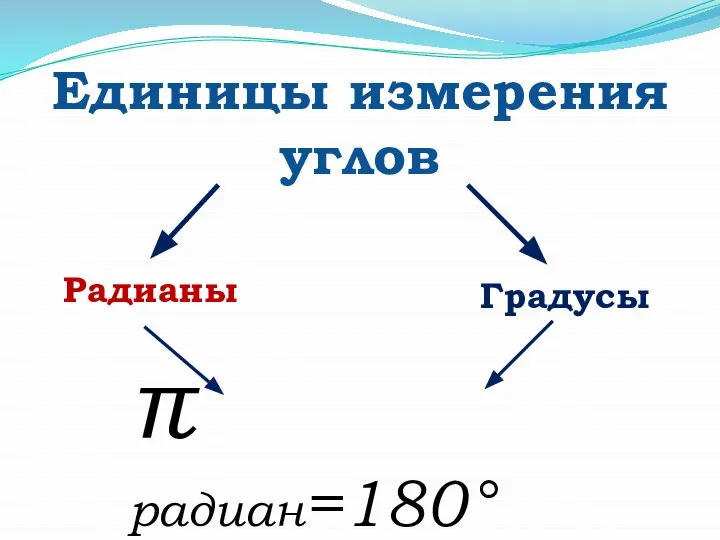
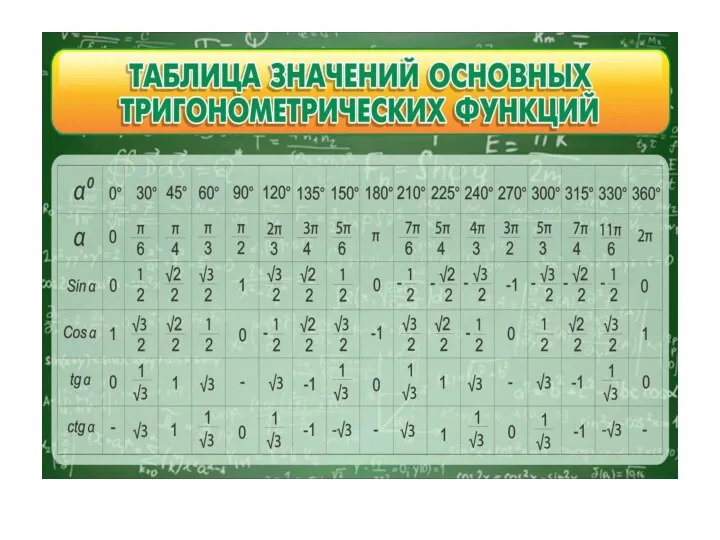
- 13. Единицы измерения углов Градусы Радианы
- 14. Градусная мера угла 1° – цена одного деления окружности, разделенной на 360 частей α=1°
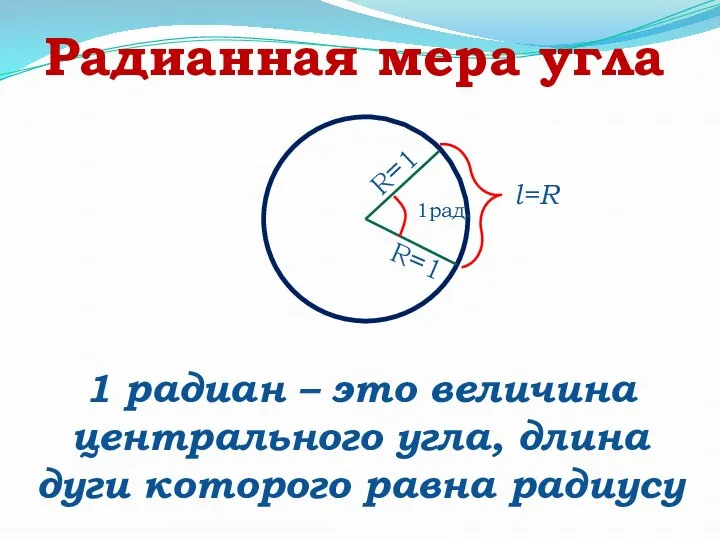
- 15. Радианная мера угла 1 радиан – это величина центрального угла, длина дуги которого равна радиусу 1рад.
- 16. Единицы измерения углов Градусы Радианы π радиан=180°
- 17. π радиан=180° Перевод из градусной меры в радианную: ⇓
- 18. Пример: 1. 2. 3.
- 19. Пример: 4. 5. 6.
- 20. Пример: 1. 2. 3.
- 21. Пример: 4. 5. 6.
- 22. π радиан=180° Перевод из радианной меры в градусную: ⇓
- 23. Пример: 1. 2. 3.
- 24. Пример: 1. 2. 3.
- 25. №1: Переведите в радианную меру углы: 1) 45° 2) 15° 3) 72° 4) 100° 5) 200°
- 26. №2: Переведите в градусную меру углы: 1) 2) 3) 4) 5) 6)
- 27. Перевод из градусной меры в радианную: Перевод из радианной меры в градусную:
- 28. Самостоятельная работа 1. Переведите в радианную меру углы: 1) 60° 2) 145° 3) 240° I вариант
- 29. Ответы 1. 1) 2) 3) I вариант II вариант 1) 2) 3) 2. 1) 72° 2)
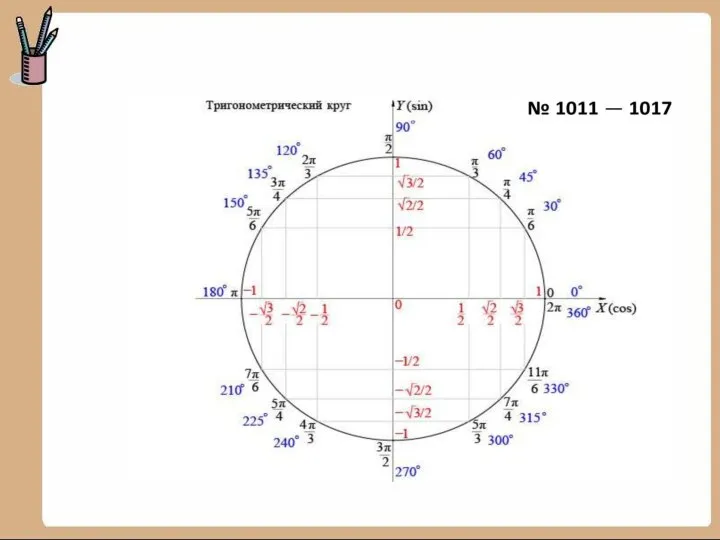
- 30. Окружность с радиусом, равным 1называется единичной. Данная окружность построена в декартовой системе координат. Радиус окружности равен
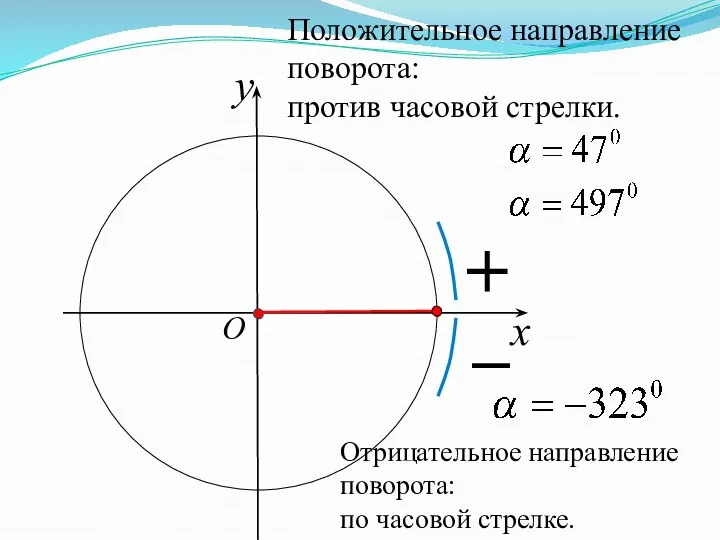
- 31. x y O Положительное направление поворота: против часовой стрелки. Отрицательное направление поворота: по часовой стрелке.
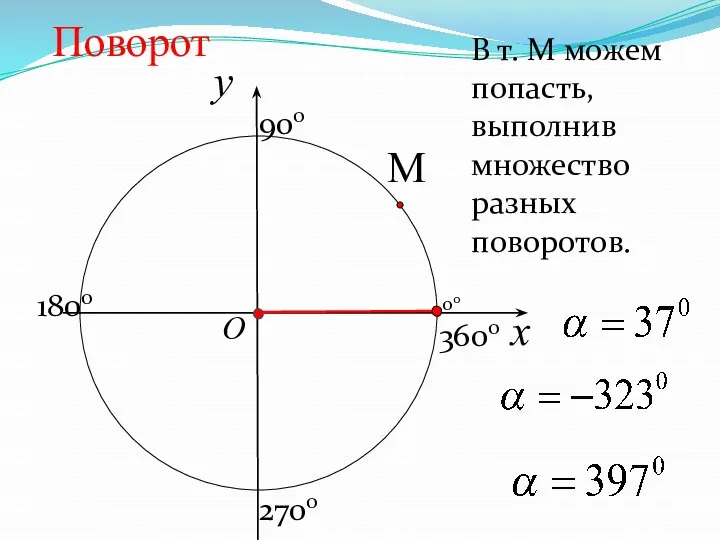
- 32. x y O Поворот В т. М можем попасть, выполнив множество разных поворотов. 900 1800 2700
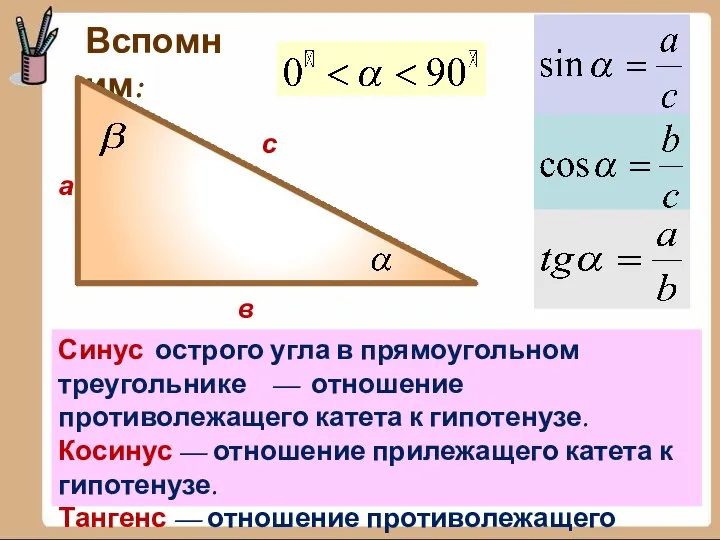
- 33. Вспомним: а в с Синус острого угла в прямоугольном треугольнике — отношение противолежащего катета к гипотенузе.
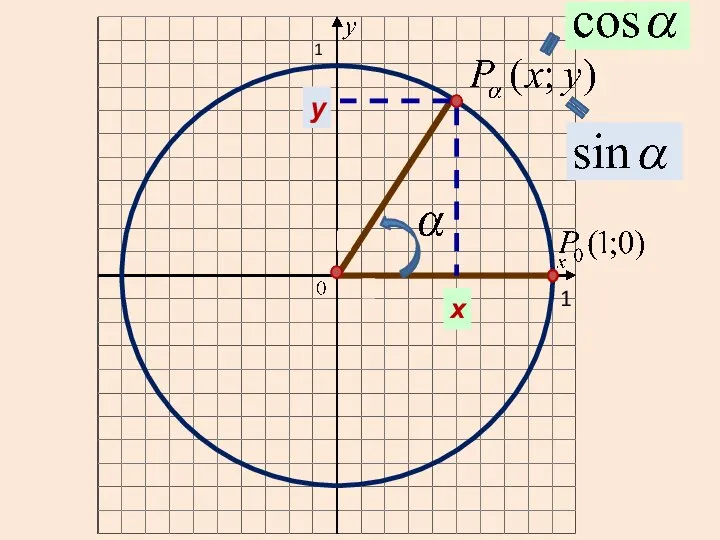
- 34. х у 1 1
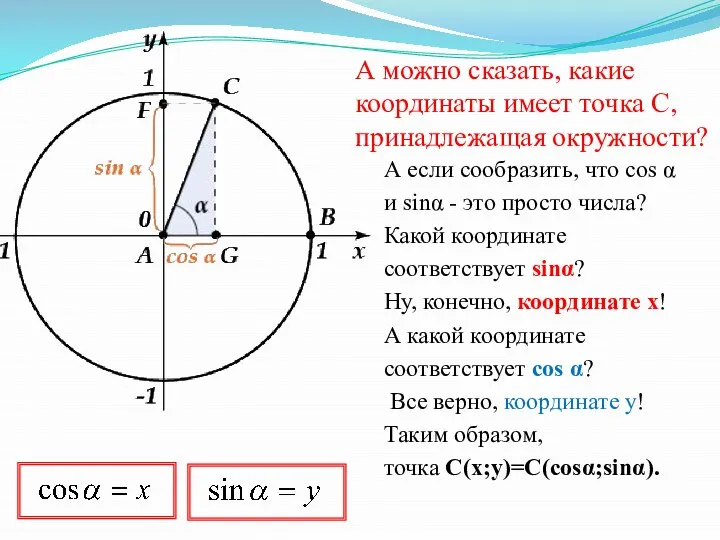
- 35. А можно сказать, какие координаты имеет точка C, принадлежащая окружности? А если сообразить, что cos α
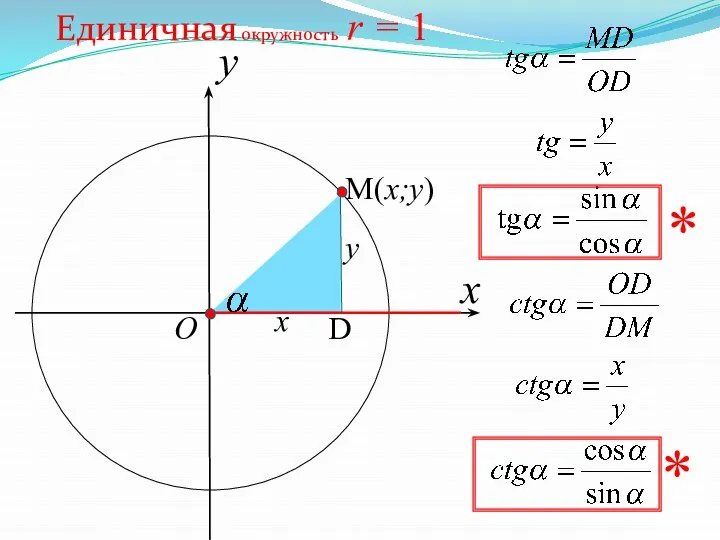
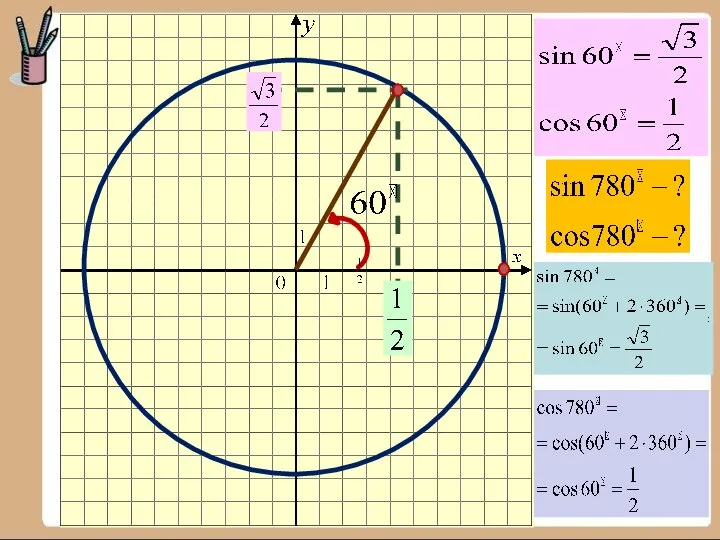
- 36. x Единичная окружность r = 1 y O x y
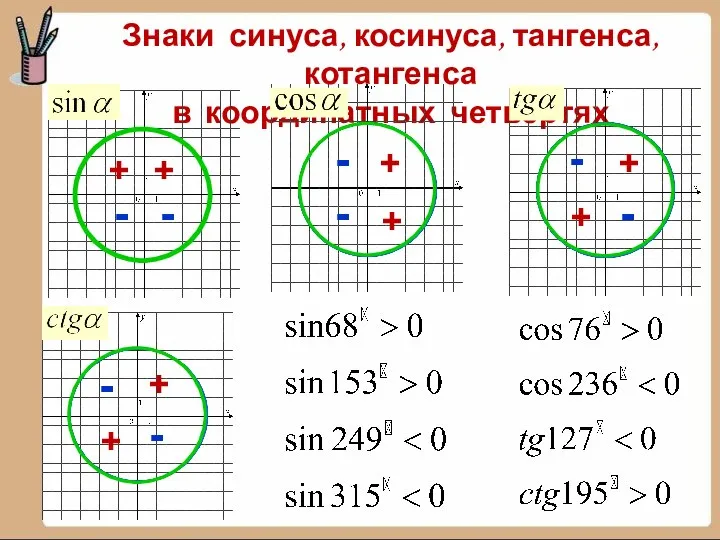
- 38. Знаки синуса, косинуса, тангенса, котангенса в координатных четвертях + + + + + + + +
- 39. Четность, нечетность синуса, косинуса, тангенса, котангенса Нечетные функции Четная функция
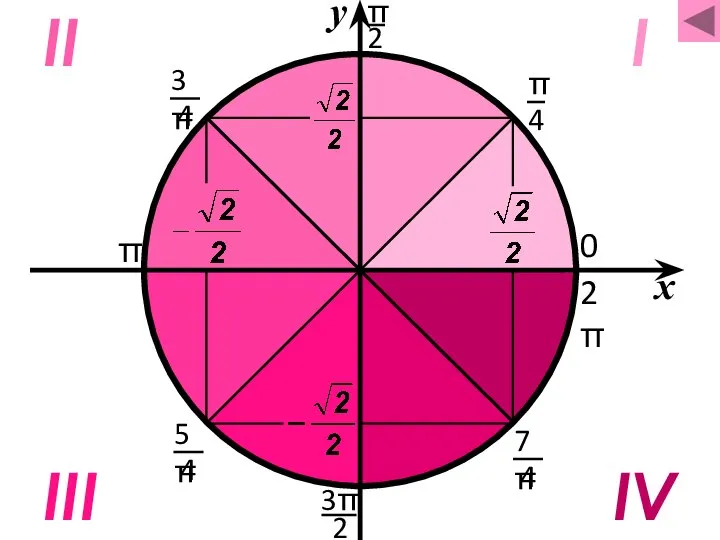
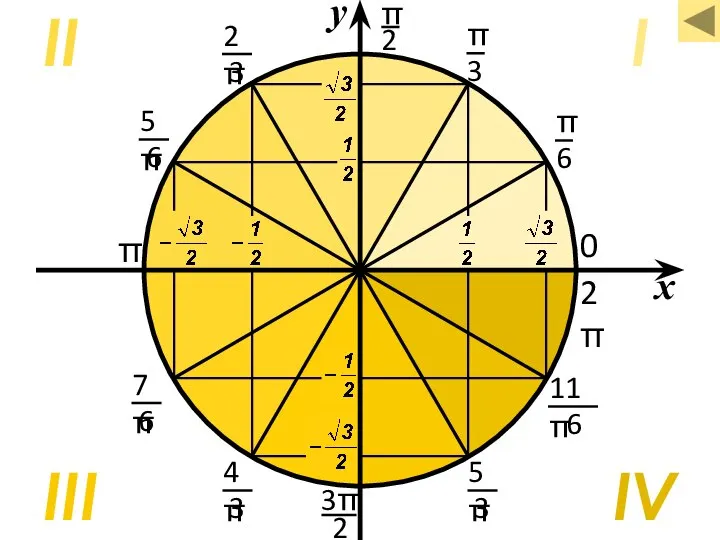
- 41. I II III IV π 2π 0 x у
- 42. x I IV II III π 2π 0 у
- 47. Домашнее задание Выучить формулы перевода из градусной меры угла в радианную и обратно. Выучить определения sin,
- 49. Скачать презентацию




























 Поверхности и тела. Проецирование геометрических фигур
Поверхности и тела. Проецирование геометрических фигур Решение простейших логарифмических неравенств
Решение простейших логарифмических неравенств Векторная алгебра. Скалярное, векторное и смешанное произведения векторов. Лекция 2
Векторная алгебра. Скалярное, векторное и смешанное произведения векторов. Лекция 2 Вектор. Равенство векторов. Откладывание вектора равного данному
Вектор. Равенство векторов. Откладывание вектора равного данному Презентация на тему Отношения и пропорции
Презентация на тему Отношения и пропорции  Перпендикуляр и наклонная к плоскости. Решение задач
Перпендикуляр и наклонная к плоскости. Решение задач Презентация на тему Статистика и математика
Презентация на тему Статистика и математика  Презентация на тему Цилиндры и цилиндрические поверхности (11 класс)
Презентация на тему Цилиндры и цилиндрические поверхности (11 класс)  Аксиома параллельных прямых
Аксиома параллельных прямых Работа с графиками функций
Работа с графиками функций Составление фигур из спичек
Составление фигур из спичек Признаки равенства треугольников
Признаки равенства треугольников Математика в кинематографии
Математика в кинематографии Погрешности измерительных приборов. Класс точности
Погрешности измерительных приборов. Класс точности Периметр восьмиугольника
Периметр восьмиугольника Базіс лінейнай прасторы. Каардынаты
Базіс лінейнай прасторы. Каардынаты Решение треугольников
Решение треугольников Симметрия относительно точки
Симметрия относительно точки Логика. Задания
Логика. Задания Презентация на тему Вычисления с многозначными числами
Презентация на тему Вычисления с многозначными числами  Неравенства. Решить систему неравенств
Неравенства. Решить систему неравенств Презентация на тему Биссектриса угла в треугольнике
Презентация на тему Биссектриса угла в треугольнике  Решение неравенств. Элективный курс. Алгебра 11 класс. Урок 3
Решение неравенств. Элективный курс. Алгебра 11 класс. Урок 3 История происхождения математических знаков
История происхождения математических знаков Открой свою звезду. Математический диктант
Открой свою звезду. Математический диктант ЕГЭ математика — профильный уровень. Задание 9
ЕГЭ математика — профильный уровень. Задание 9 Дифуры 1 порядка
Дифуры 1 порядка Матрицы
Матрицы