Содержание
- 2. Утверждения утверждения определяют истинность или ложность составных высказываний, не вникая в их содержание
- 3. Высказывания Любое утверждение, относительно которого имеет смысл говорить, сто оно истинно или ложно, называют высказыванием. Высказывания
- 4. В алгебре высказываний над логическими переменными (над высказываниями) можно производить определенные логические операции, в результате которых
- 5. Составные высказывания Высказывания, состоящие из нескольких простых суждений и содержащие в себе более, чем одну простую
- 6. Логические операции Конъюнкция (логическое умножение, «И») Дизъюнкция (логическое сложение, «ИЛИ») Инверсия (логическое отрицание, «НЕ») Импликация (логическое
- 7. Объединение двух или нескольких высказываний в одно с помощью союза «И» называется логическим умножением, или конъюнкцией
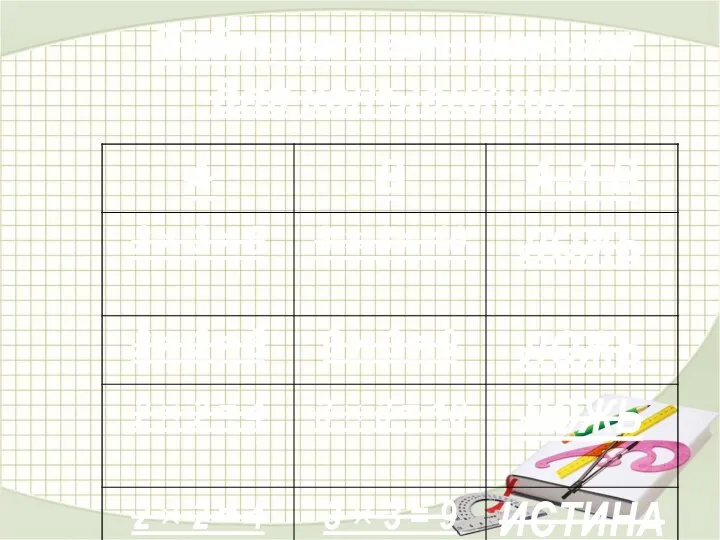
- 8. Конъюнкция. Определите истинность. «2 × 2 = 5» И «3 × 3 = 10» «2 ×
- 9. Запись конъюнкции на формальном языке алгебры высказываний F(A,B) = A ∧ B
- 10. Таблица истинности показывает какие значения принимает логическая функция при всех возможных значениях логических переменных
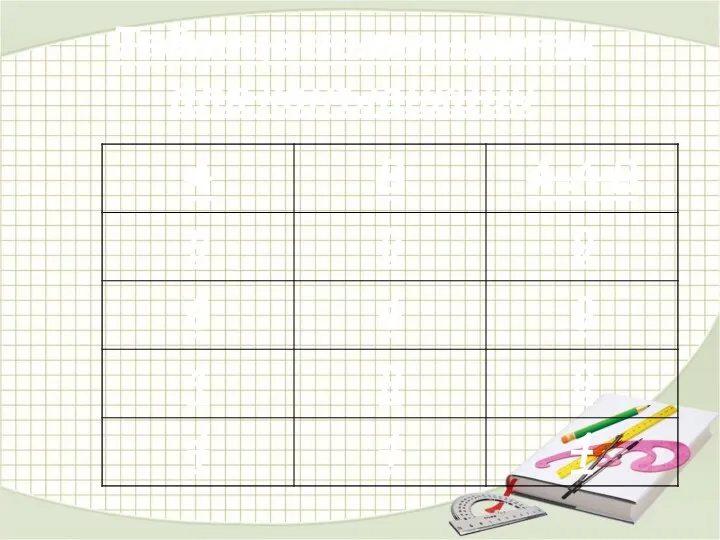
- 11. Таблица истинности для конъюнкции
- 12. Таблица истинности для конъюнкции
- 13. Объединение двух или нескольких высказываний в одно с помощью союза «ИЛИ» называется логической суммой, или дизъюнкцией
- 14. Логическая функция, полученная в результате дизъюнкции, истинна тогда, когда истинна хотя бы одна из входящих в
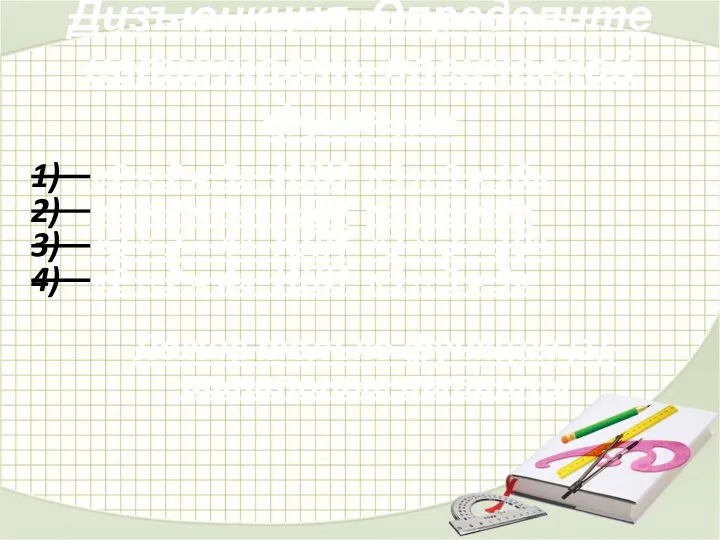
- 15. Дизъюнкция. Определите истинность логической функции «2 × 2 = 5» ИЛИ «3 × 3 = 10»
- 16. Запись дизъюнкции на формальном языке алгебры высказываний F(A,B) = A ∨ B Также может встретиться запись,
- 17. Таблица истинности для дизъюнкции
- 18. Таблица истинности для дизъюнкции
- 19. Дополнительные логические функции Импликацию и эквивалентность можно выразить через конъюнкцию, дизъюнкцию и отрицание, поэтому их называют
- 20. Объединение двух высказываний, из которых первое является условием, а второе – следствием из него, называется импликацией
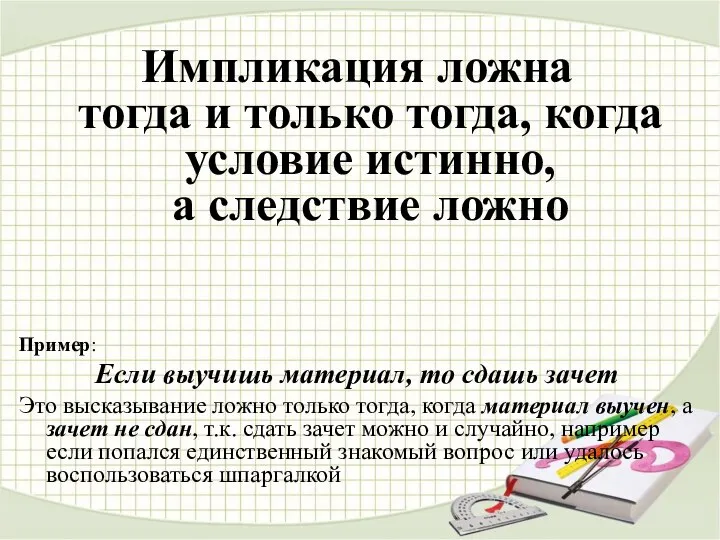
- 21. Импликация ложна тогда и только тогда, когда условие истинно, а следствие ложно Пример: Если выучишь материал,
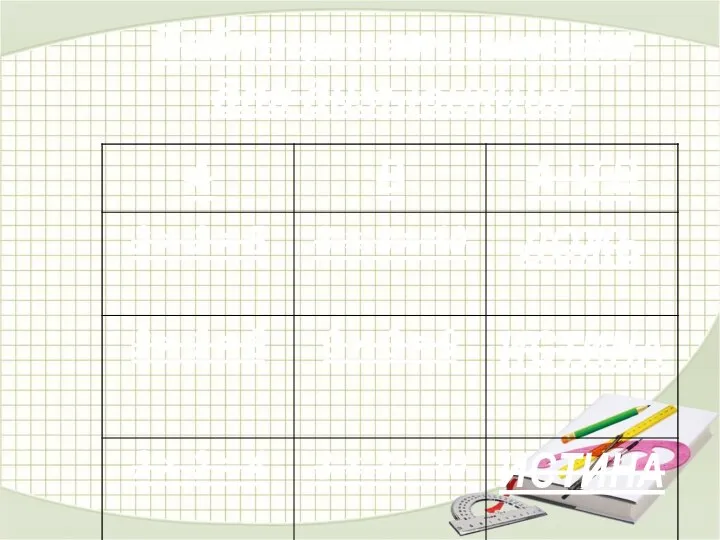
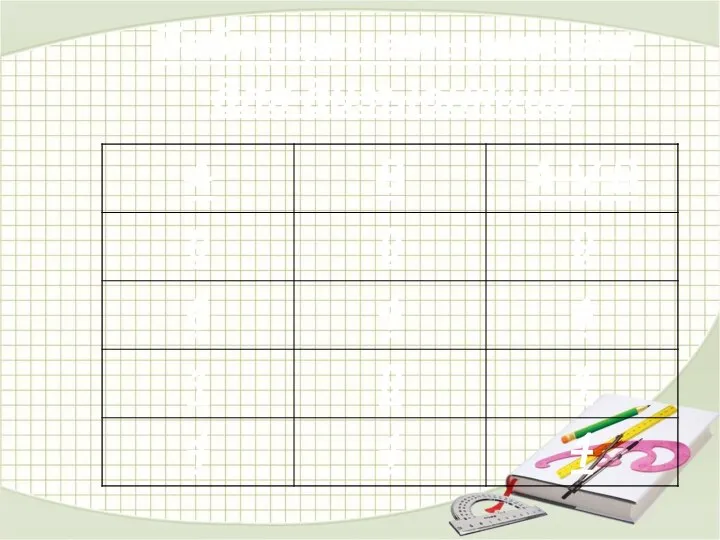
- 22. Таблица истинности для импликации
- 23. Эквивалентность – это логическая операция, объединяющая два простых высказывания в одно составное и которое является истинным
- 24. Таблица истинности для эквивалентности
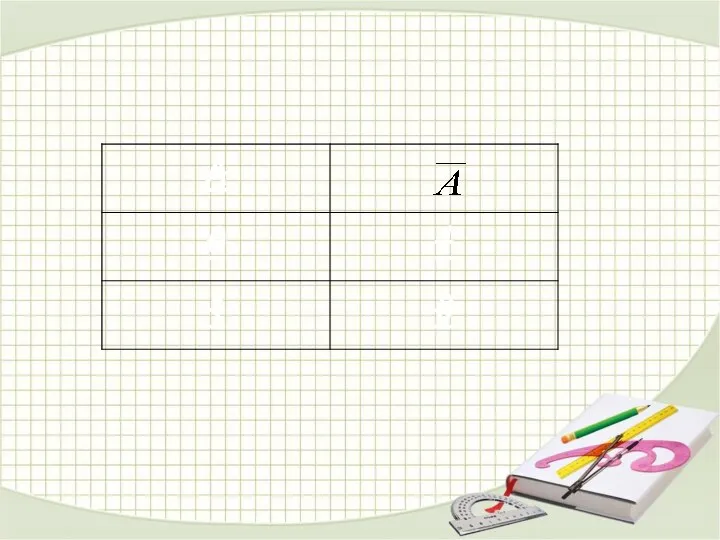
- 25. Отрицанием высказывания А называют высказывание, которое истинно, если высказывание А ложно, и ложно, если высказывание А
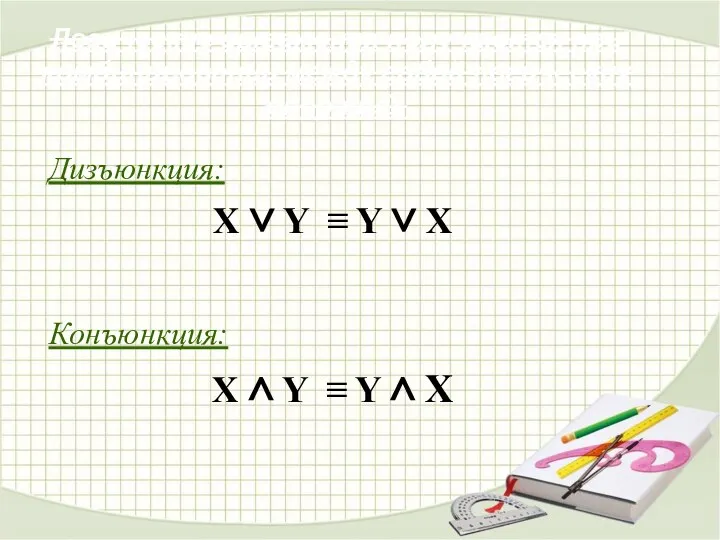
- 27. Дизъюнкция: X ∨ Y ≡ Y ∨ X Конъюнкция: X ∧ Y ≡ Y ∧ X
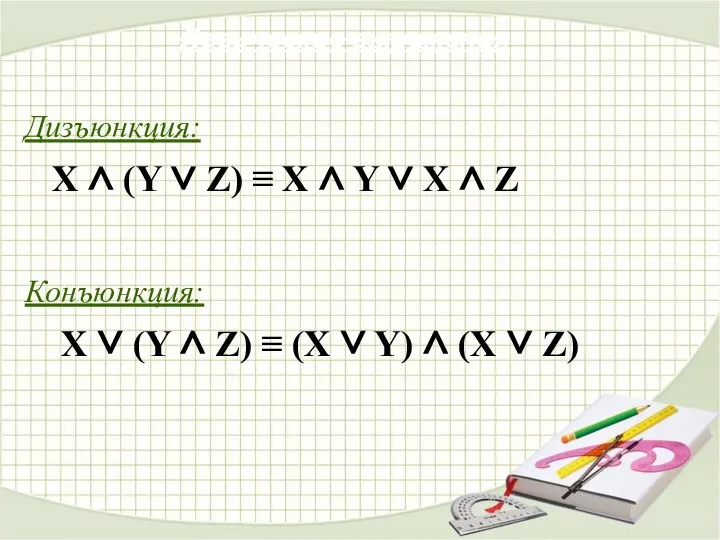
- 28. Дизъюнкция: X ∨ (Y ∨ Z) ≡ (X ∨ Y) ∨ Z Конъюнкция: X ∧ (Y
- 29. Дизъюнкция: X ∧ (Y ∨ Z) ≡ X ∧ Y ∨ X ∧ Z Конъюнкция: X
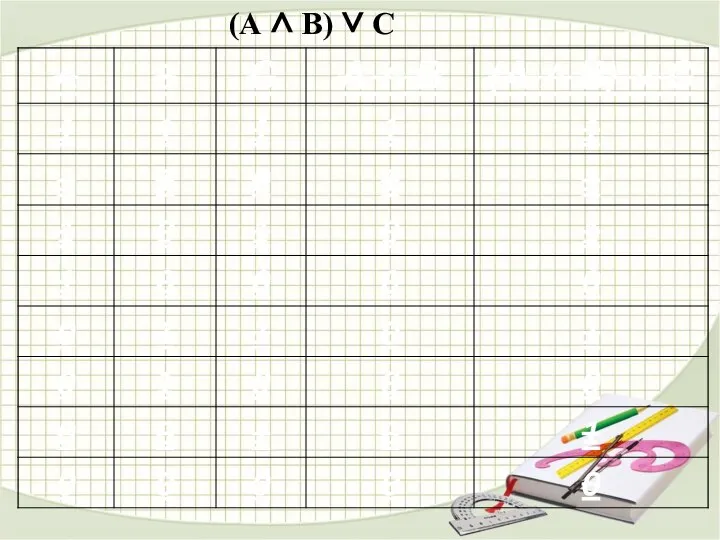
- 30. (А ∧ В) ∨ С
- 31. Высказывание А и В называют логически эквивалентными, если они или оба истинны, или оба ложны.
- 33. Скачать презентацию











 Предмет стереометрии. Аксиомы стереометрии
Предмет стереометрии. Аксиомы стереометрии Анимированный плакат Цифры – прописи
Анимированный плакат Цифры – прописи Математико-картографическое моделирование
Математико-картографическое моделирование Пропорциональные отрезки в прямоугольном треугольнике
Пропорциональные отрезки в прямоугольном треугольнике Верхняя, нижняя сумма Дарбу
Верхняя, нижняя сумма Дарбу Функции и графики
Функции и графики Умножение на 1. Проведите динозаврика по лабиринту (1)
Умножение на 1. Проведите динозаврика по лабиринту (1) Доли. Обыкновенные дроби
Доли. Обыкновенные дроби Тригонометрические Функции
Тригонометрические Функции Первый признак подобия треугольников
Первый признак подобия треугольников Признаки равенства треугольников
Признаки равенства треугольников Объём параллелепипеда. Задачи
Объём параллелепипеда. Задачи Задачи на движение в противоположных направлениях
Задачи на движение в противоположных направлениях Симметрия. Виды симметрии
Симметрия. Виды симметрии Состав чисел первого десятка
Состав чисел первого десятка Решение типовых задач Параллельность прямых и плоскостей
Решение типовых задач Параллельность прямых и плоскостей Презентация по математике "Приемы вычислений для случаев вида 60-24" -
Презентация по математике "Приемы вычислений для случаев вида 60-24" -  Міри маси, часу, довжини
Міри маси, часу, довжини Решение квадратных уравнений по формуле. Алгебра, 8 класс
Решение квадратных уравнений по формуле. Алгебра, 8 класс В мире геометрии
В мире геометрии Сумма углов треугольника
Сумма углов треугольника Доли. Обыкновенные дроби. 5 класс
Доли. Обыкновенные дроби. 5 класс 70 задач на чертежах по планиметрии
70 задач на чертежах по планиметрии Решение неравенств методом интервалов
Решение неравенств методом интервалов Число и цифра 2
Число и цифра 2 От землемерия к геометрии
От землемерия к геометрии Линейная алгебра. (Матрицы, определители)
Линейная алгебра. (Матрицы, определители) pril1
pril1