Содержание
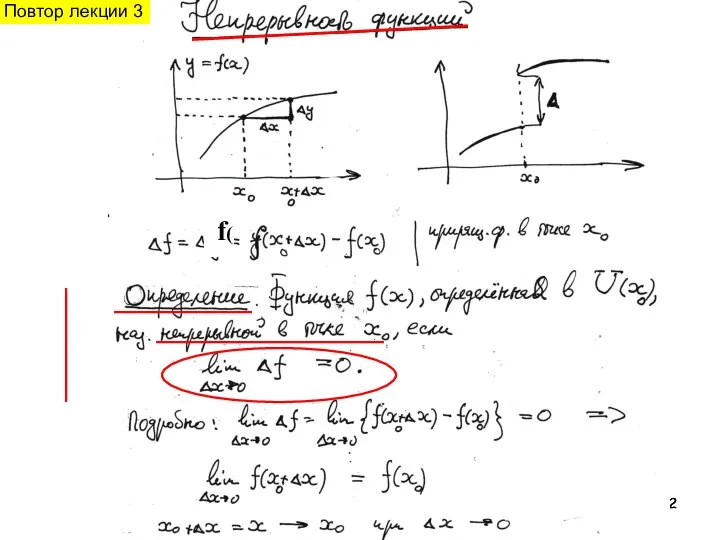
- 2. f( Повтор лекции 3
- 3. . Таким образом, приходим к важнейшему понятию : Определение. Пусть ф. f(x) определена в окр. т.
- 4. . ⎯⎯⎯⎯⎯⎯⎯ ⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯ ⎯⎯⎯ наз. предельное положение секущей при P M
- 5. Производная сложной функции Повтор лекции 4
- 6. Дифференциал функции Повтор лекции 4
- 7. Основные теоремы дифференциального исчисления Повтор лекции 5
- 8. нет локального экстремума! 1
- 9. по 2-й т. Вейерштасса по т. Ферма (слайд №11) 2
- 10. 3
- 11. 4
- 12. Правило Лопиталя-Бернулли Теорема тогда ⇒ ) х)
- 13. ) )
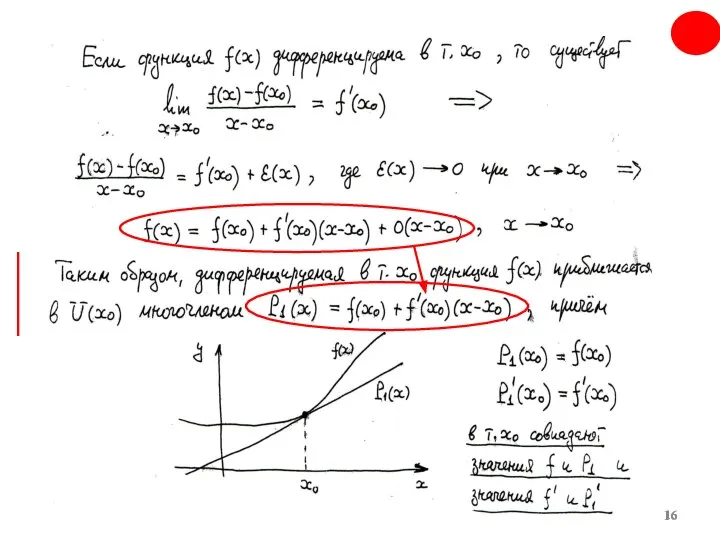
- 15. Формула Тейлора является одной из жемчужин математического анализа и широко используется и в теоретических исследованиях, и
- 17. n n _____________ Форма Пеано
- 18. Сл №26
- 20. ≡≡≡ 1 2 3 3
- 21. Продолжение 4 5
- 22. ) Вычисление пределов по формуле Тейлора см. слайд №20-21
- 23. n !
- 24. и нж Форма Пеано см. сл.15
- 25. −−−−−−−− _____
- 27. (см.сл №7)
- 28. Локальные экстремумы Из теоремы Ферма следует
- 29. Теорема (первый дост. признак строгого лок. экстремума в крит. точке) Пусть f(x) – дифференцируема в U(x
- 31. Теорема (2-й дост. признак строгого лок. экстремума ) __________________
- 33. Продолжение
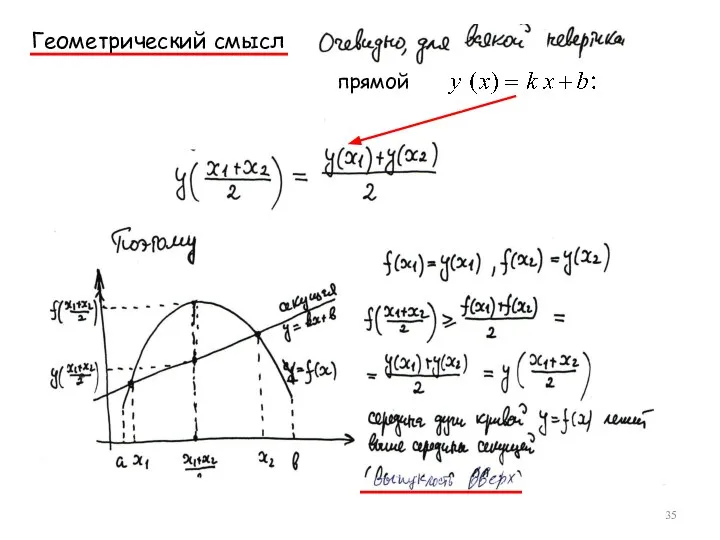
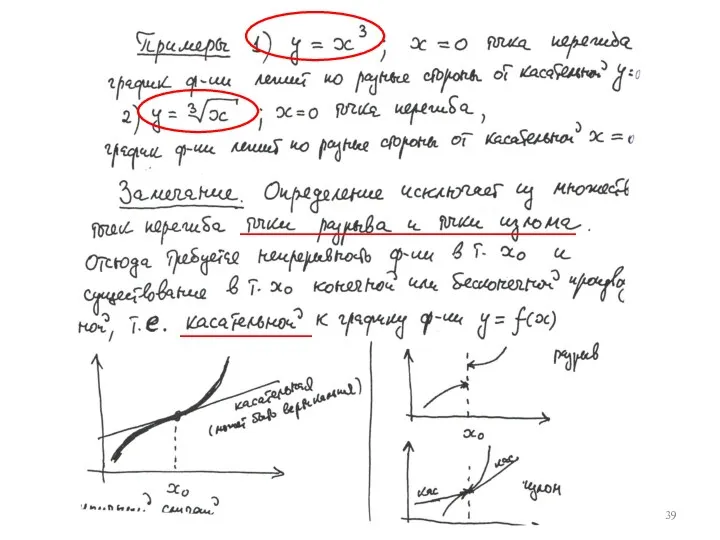
- 35. Геометрический cмысл прямой
- 36. 2
- 44. Таблица поведения функции Схема построения графиков
- 46. Спасибо за внимание
- 48. Скачать презентацию















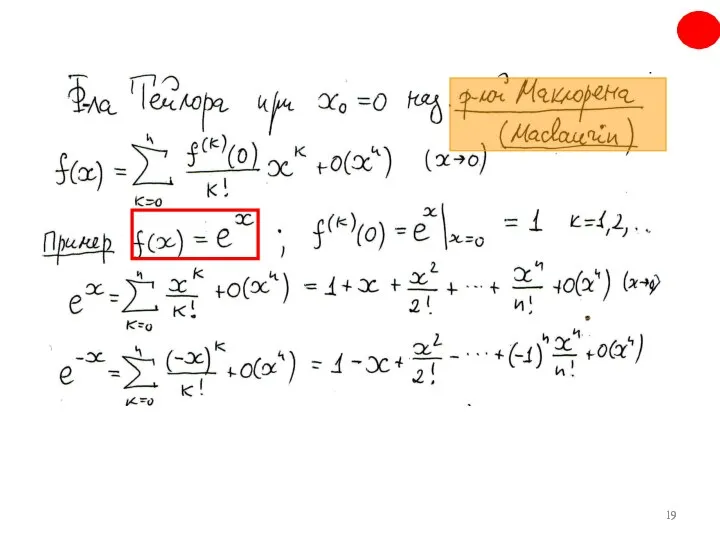

























 Построение сечения многогранника плоскостью
Построение сечения многогранника плоскостью Деление и умножение на 2
Деление и умножение на 2 Различные виды тестирования при изучении темы Десятичные дроби
Различные виды тестирования при изучении темы Десятичные дроби Решение уравнений
Решение уравнений Презентация на тему Построение точек по заданным координатам
Презентация на тему Построение точек по заданным координатам  Функция y=sin x, её свойства и график
Функция y=sin x, её свойства и график Стереометрия. Теория
Стереометрия. Теория Решение задач с помощью систем
Решение задач с помощью систем Тригонометрия в биологии и медицине
Тригонометрия в биологии и медицине Решение задач к главе IV §1,2
Решение задач к главе IV §1,2 Разнообразный мир линий
Разнообразный мир линий Riņķa līnija un daudzstūri
Riņķa līnija un daudzstūri Окружность, круг, их элементы и части. Центральный угол
Окружность, круг, их элементы и части. Центральный угол Скалярное произведение векторов
Скалярное произведение векторов Лабиринты. Решение найденных лабиринтов и поиск универсальных правил
Лабиринты. Решение найденных лабиринтов и поиск универсальных правил Титло
Титло Презентация на тему Графики тригонометрических функций
Презентация на тему Графики тригонометрических функций  Многогранники
Многогранники Правила вычисления производной
Правила вычисления производной جمع%20و%20تفریق%20اعداد%20مرکب%20و%20الگوها
جمع%20و%20تفریق%20اعداد%20مرکب%20و%20الگوها Вычисление длины дуги
Вычисление длины дуги Квадратный корень из степени
Квадратный корень из степени 29.09 Решение задач
29.09 Решение задач Преобразование выражения Asinx+Bcosx к виду Csin(x+t)
Преобразование выражения Asinx+Bcosx к виду Csin(x+t) В мире треугольников. (1) 7 класс
В мире треугольников. (1) 7 класс Решение задач по геометрии
Решение задач по геометрии Упрощение логических выражений
Упрощение логических выражений Функции и их свойства. Квадратный трехчлен
Функции и их свойства. Квадратный трехчлен