Содержание
- 2. Обсуждаемые вопросы Точность статистического анализа в зависимости от объема текста. Идентификация автора неизвестного текста в библиотеке
- 3. Обсуждаемые вопросы Анализ авторских тандемов и проверка текста на однородность. Динамические системы, генерирующие ряд расстояний между
- 4. Цель и программа работы Сопоставление тексту структуры в фазовом пространстве (букв, слов и т.п.) Введение нормы
- 5. Текстовый инвариант? – Нет! Текстовый инвариант – это функционал F(T) от текстовой структуры. Два текста близки
- 6. 1. Статистическая достоверность определения частот употребления букв в литературных произведениях
- 7. Выборочное распределение текста по буквам Пусть ξ – случайная величина (буква или буквосочетание), принимающая значения из
- 8. Минимально достаточная длина текста Тексты должны быть таких длин, чтобы статистическая неопределенность в оценке вероятностей буквосочетаний
- 9. Оценка достаточной длины текста Для стационарного процесса оценка среднего при неизвестной дисперсии дается статистикой Стьюдента Оценка
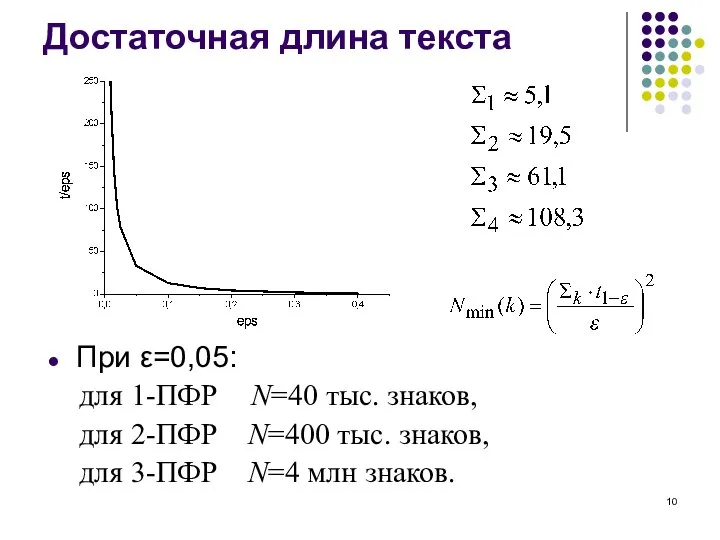
- 10. Достаточная длина текста При ε=0,05: для 1-ПФР N=40 тыс. знаков, для 2-ПФР N=400 тыс. знаков, для
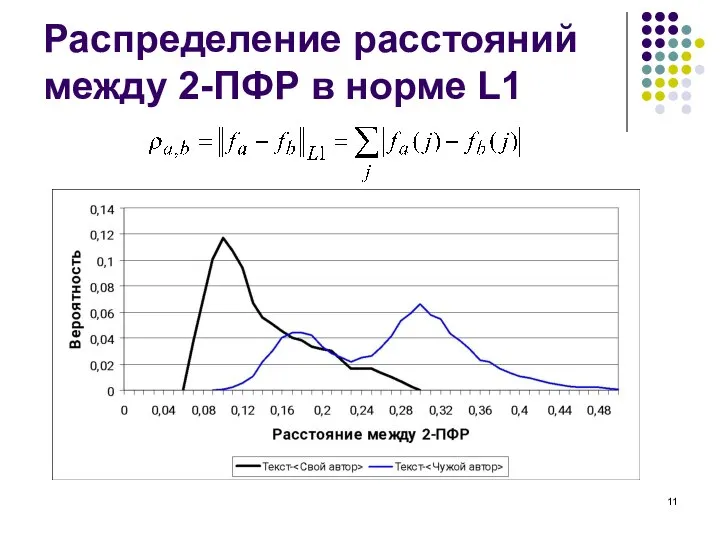
- 11. Распределение расстояний между 2-ПФР в норме L1
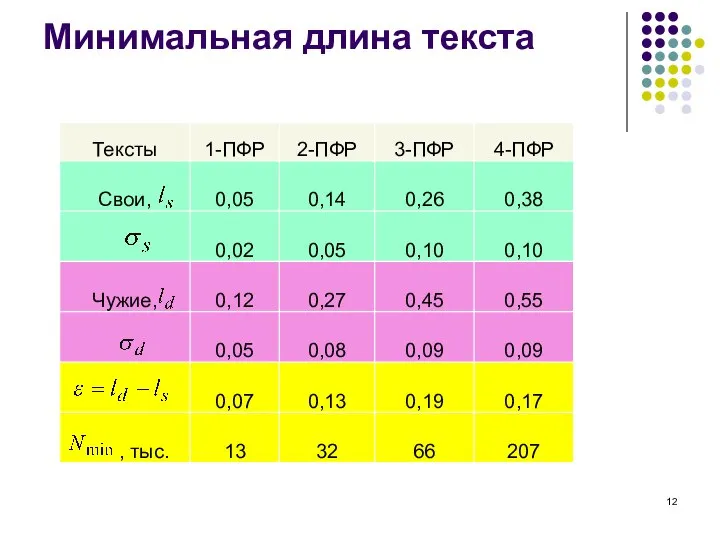
- 12. Минимальная длина текста
- 13. Уровень нестационарности текстов Расстояние между ПФР текстов: Чтобы сравнивать распределения текстов разных объемов, следует убедиться в
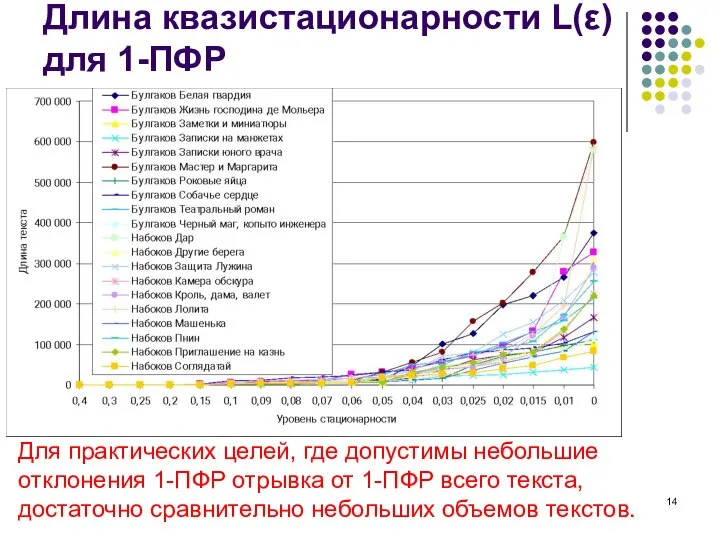
- 14. Длина квазистационарности L(ε) для 1-ПФР Для практических целей, где допустимы небольшие отклонения 1-ПФР отрывка от 1-ПФР
- 15. 2. Кластеризация текстов, создание эталонных распределений и метод идентификации автора
- 16. Идентификация автора текста Пусть имеется библиотека из A авторов, у a-го автора текстов, в i-ом тексте
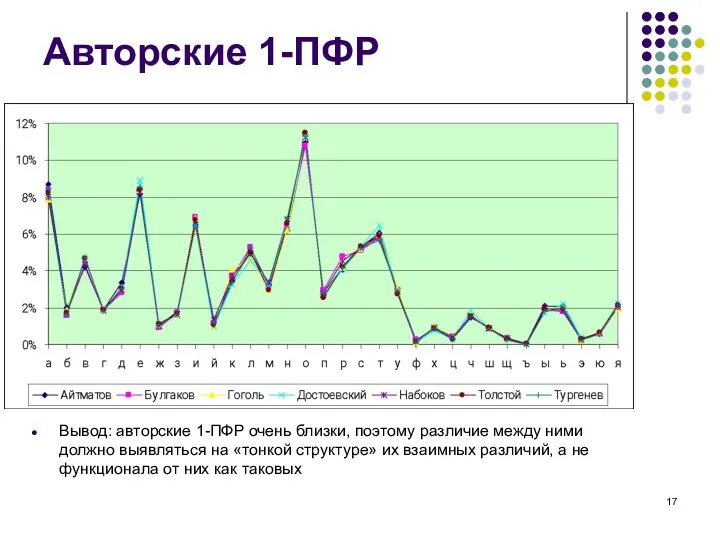
- 17. Авторские 1-ПФР Вывод: авторские 1-ПФР очень близки, поэтому различие между ними должно выявляться на «тонкой структуре»
- 18. Ошибки 1-го и 2-го родов функция распределения расстояний текстов автора от его эталона; чужих текстов от
- 19. Мощность статистических методов идентификации автора
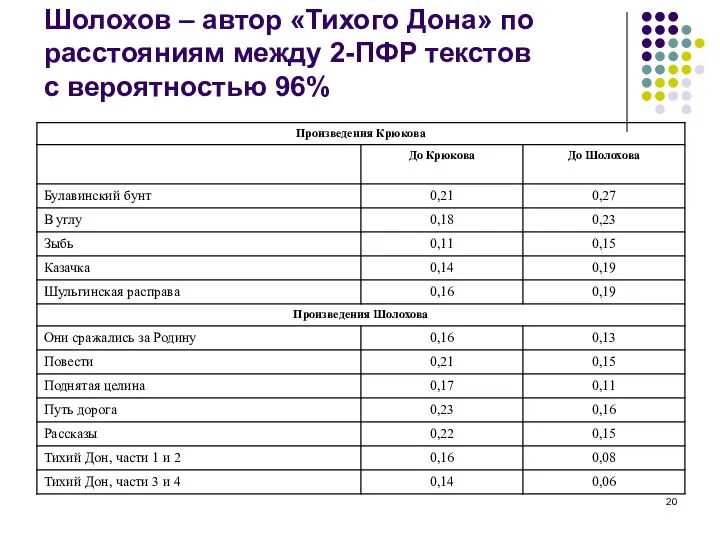
- 20. Шолохов – автор «Тихого Дона» по расстояниям между 2-ПФР текстов с вероятностью 96%
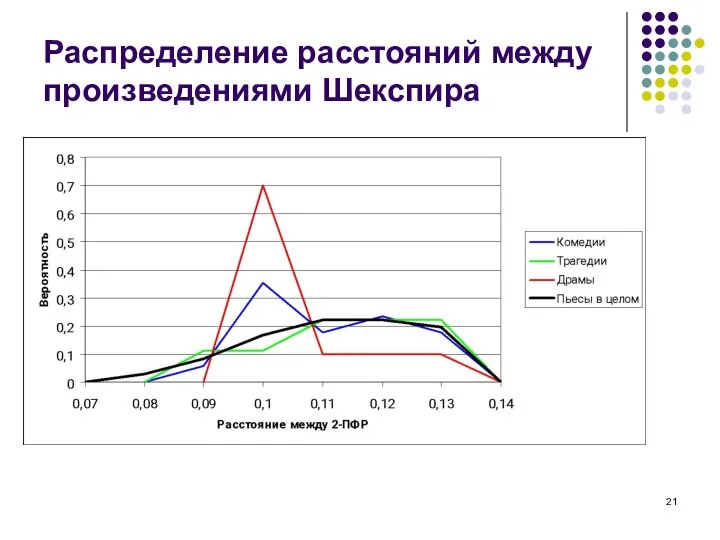
- 21. Распределение расстояний между произведениями Шекспира
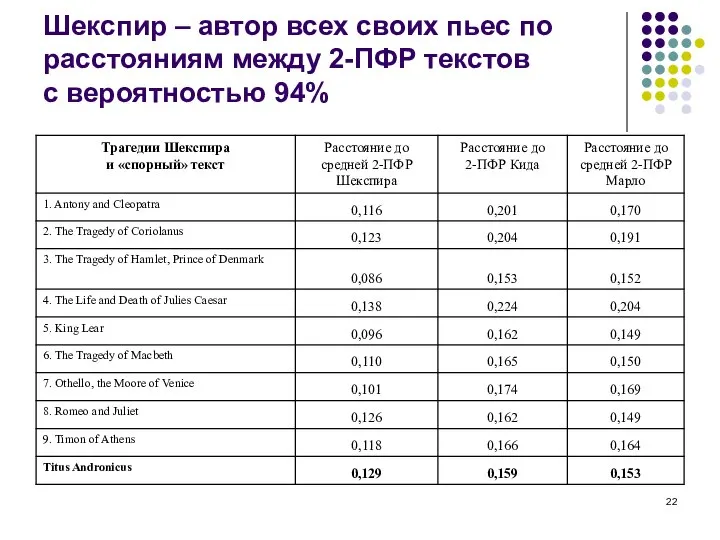
- 22. Шекспир – автор всех своих пьес по расстояниям между 2-ПФР текстов с вероятностью 94%
- 23. 3. Спектральные портреты авторов и эффект переводчика
- 24. Оператор трансляций Пусть есть условная вероятность того, что буква следует за буквой . Пусть также есть
- 25. Оператор трансляций на 1 шаг выражается через 1-ПФР и 2-ПФР: По формуле полной вероятности Следовательно, 1-ПФР
- 26. ε-спектр оператора соседних трансляций Число λ называется принадлежащим ε-спектру матрицы P, если существует матрица Δ такая,
- 27. Вычисление ε-спектра Параметром дихотомии спектра относительно кривой называется норма квадрата резольвенты на данной кривой: Если на
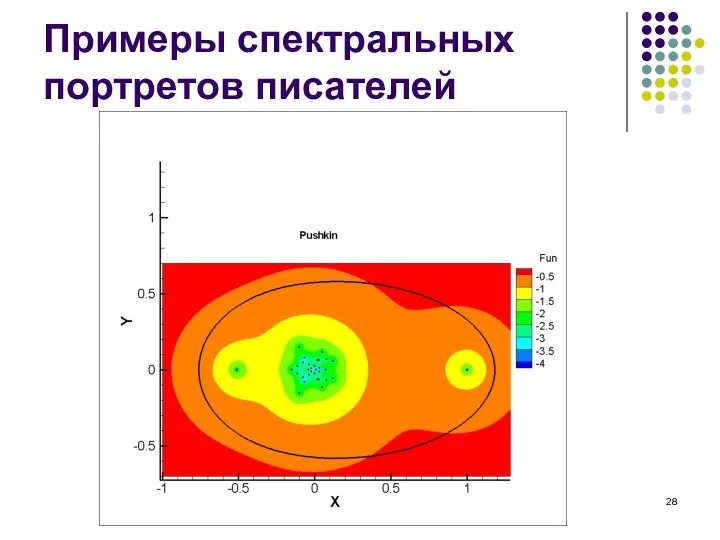
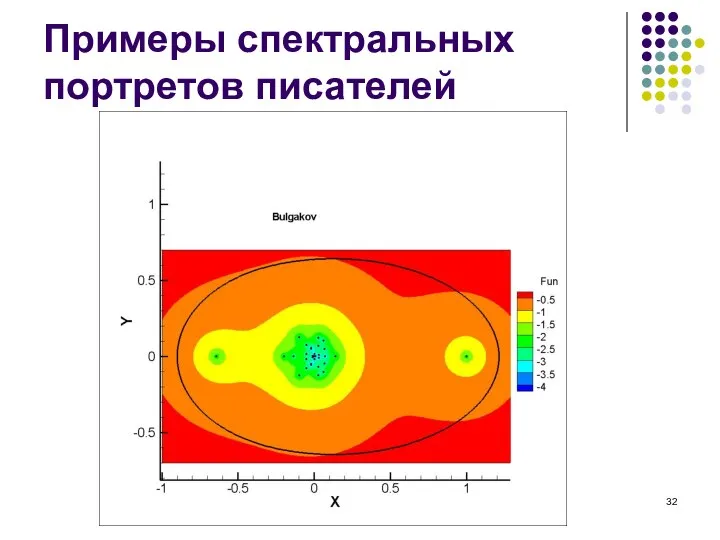
- 28. Примеры спектральных портретов писателей
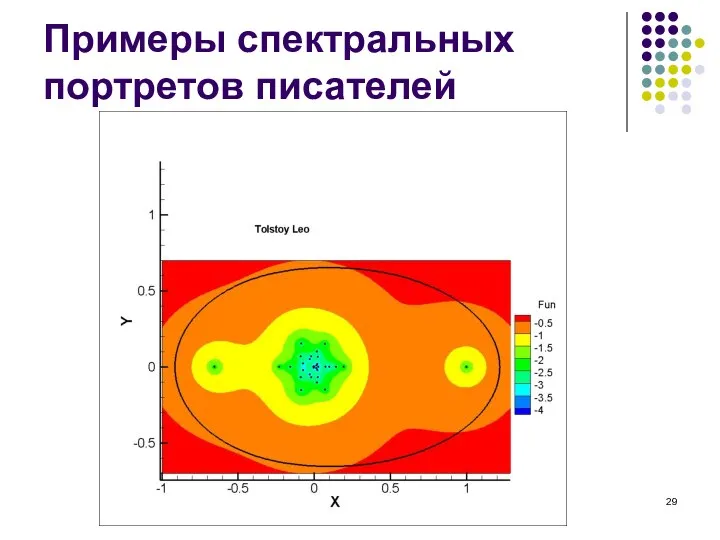
- 29. Примеры спектральных портретов писателей
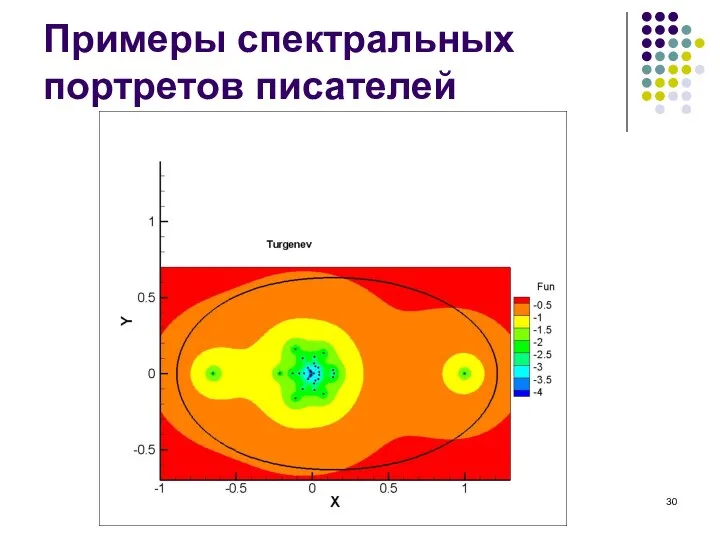
- 30. Примеры спектральных портретов писателей
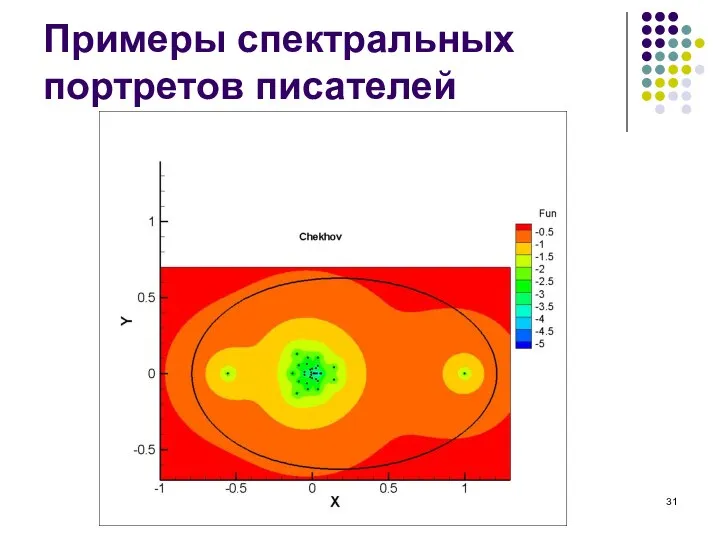
- 31. Примеры спектральных портретов писателей
- 32. Примеры спектральных портретов писателей
- 33. Эффект переводчика и вектор «подсознания» Кроме с.з. , которому отвечает с.в. 1-ПФР f , у оператора
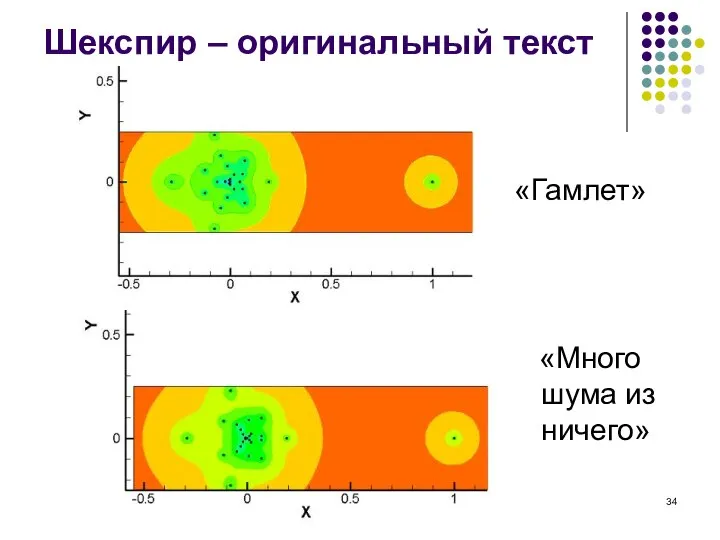
- 34. Шекспир – оригинальный текст «Гамлет» «Много шума из ничего»
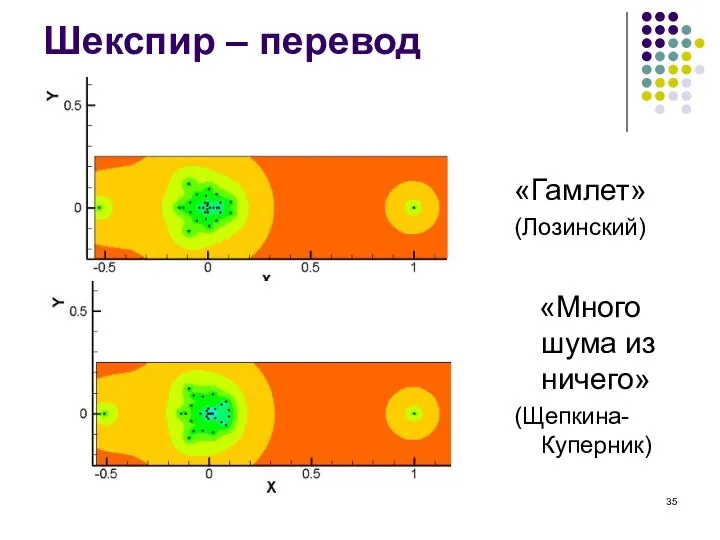
- 35. Шекспир – перевод «Гамлет» (Лозинский) «Много шума из ничего» (Щепкина-Куперник)
- 36. 4. Анализ авторских тандемов и проверка текста на однородность
- 37. Горизонтный ряд Пусть x(t) – эквидистантный временной ряд, f(N,t) – его ВПФР, построенная к моменту t
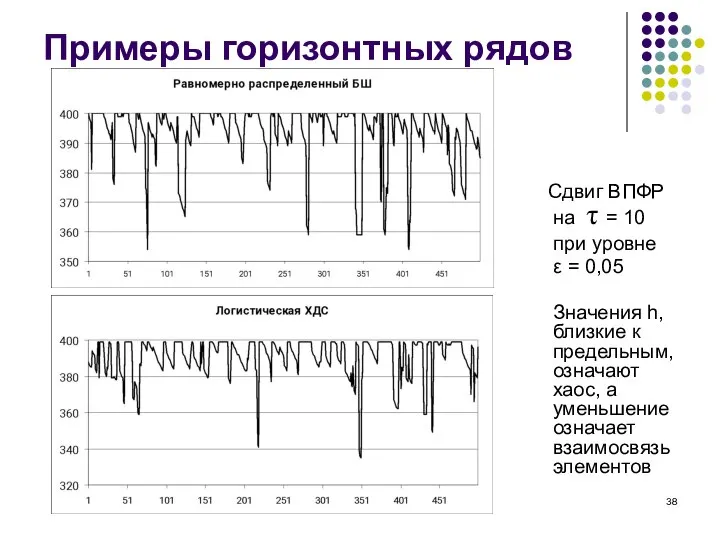
- 38. Примеры горизонтных рядов Сдвиг ВПФР на τ = 10 при уровне ε = 0,05 Значения h,
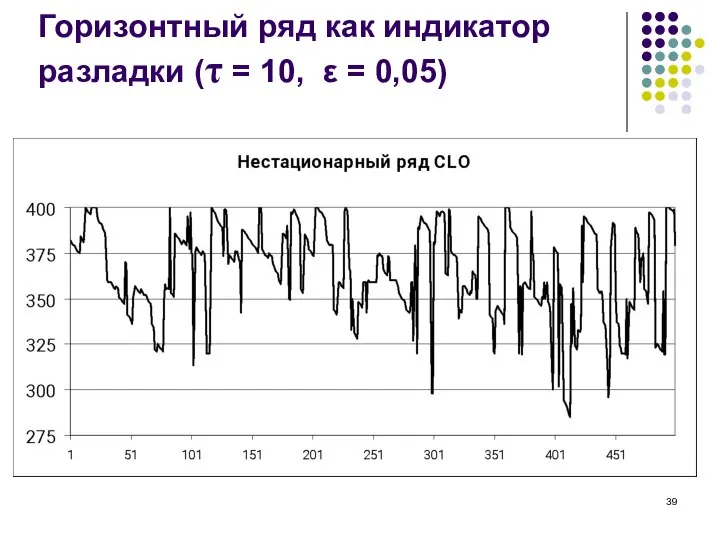
- 39. Горизонтный ряд как индикатор разладки (τ = 10, ε = 0,05)
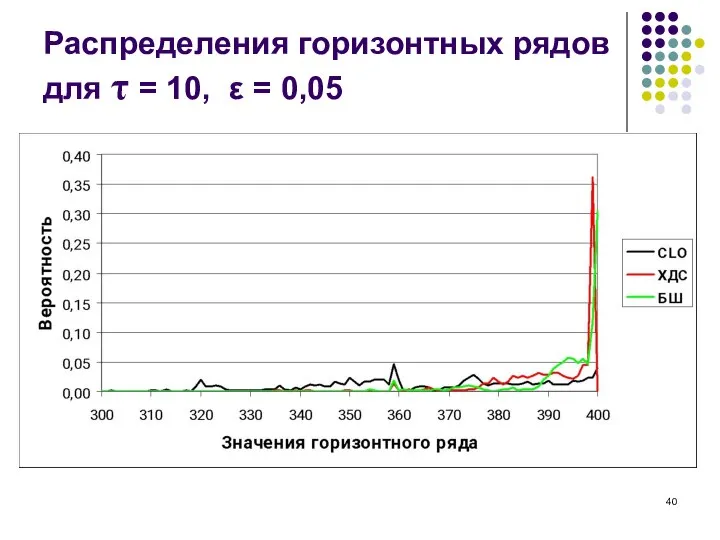
- 40. Распределения горизонтных рядов для τ = 10, ε = 0,05
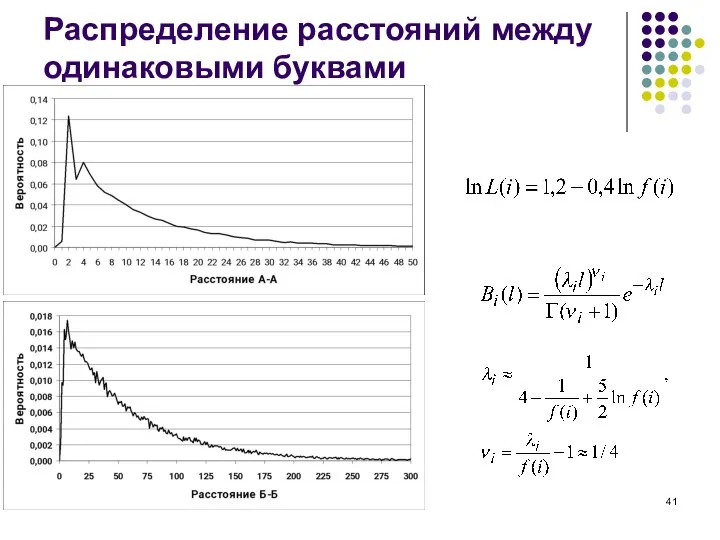
- 41. Распределение расстояний между одинаковыми буквами
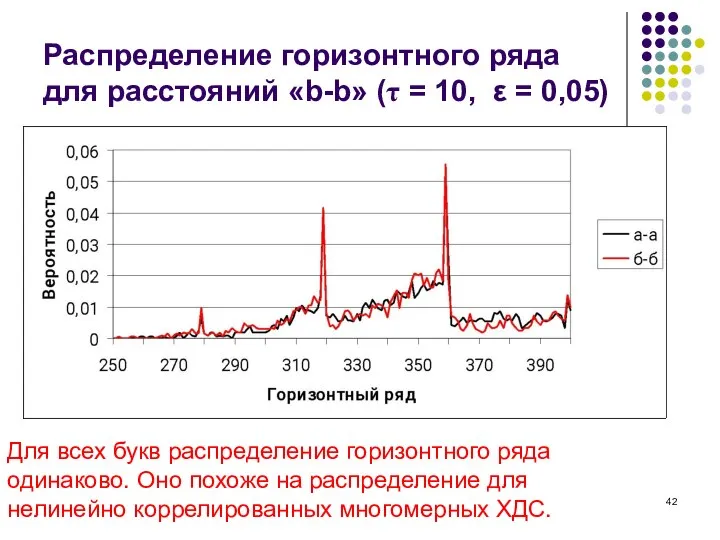
- 42. Распределение горизонтного ряда для расстояний «b-b» (τ = 10, ε = 0,05) Для всех букв распределение
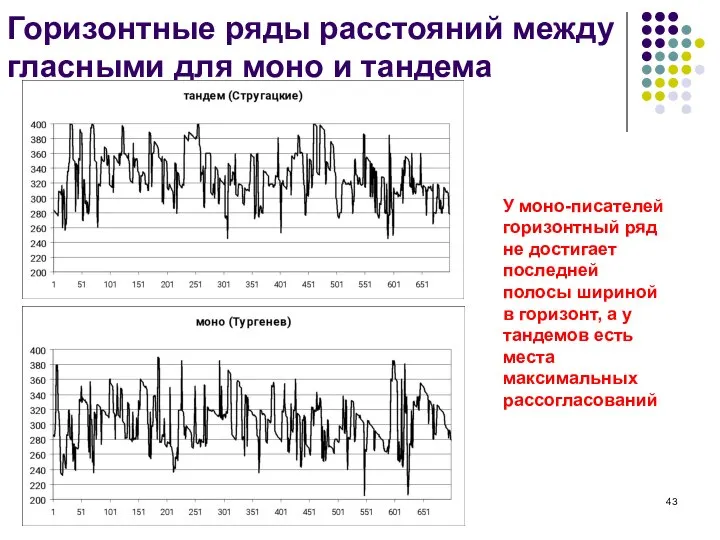
- 43. Горизонтные ряды расстояний между гласными для моно и тандема У моно-писателей горизонтный ряд не достигает последней
- 44. 5. Упорядоченность букв по частоте встречаемости в европейских языках
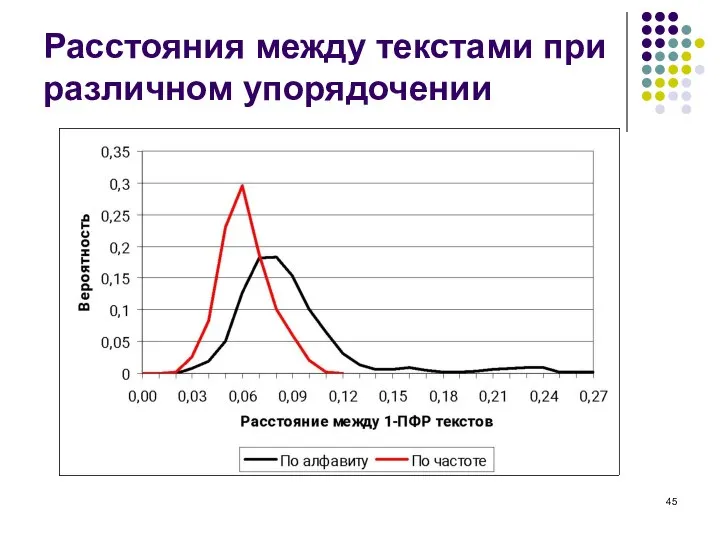
- 45. Расстояния между текстами при различном упорядочении
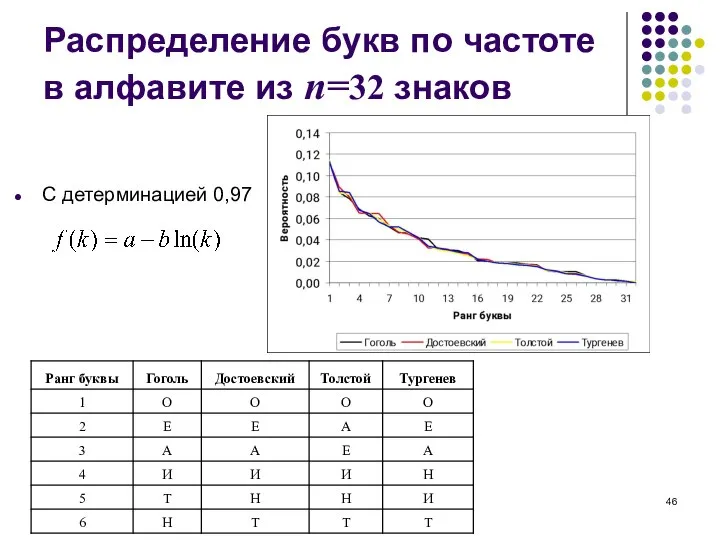
- 46. Распределение букв по частоте в алфавите из n=32 знаков С детерминацией 0,97
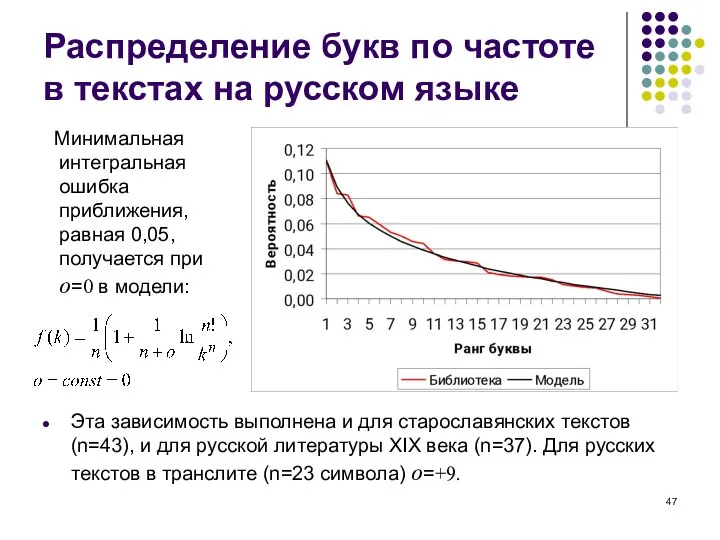
- 47. Распределение букв по частоте в текстах на русском языке Минимальная интегральная ошибка приближения, равная 0,05, получается
- 48. Избыточность и недостаточность алфавитов европейских языков Параметр o трактуем как оценку избыточности (o 0) алфавита по
- 49. Основные результаты 3-ПФР представляет ту текстовую структуру, расстояние в которой позволяет с высокой точностью опознавать автора
- 51. Скачать презентацию
























 Презентация на тему Площадь треугольника
Презентация на тему Площадь треугольника  Координаты вектора
Координаты вектора Примеры на сложение
Примеры на сложение Число 10
Число 10 Вероятность события (часть 3)
Вероятность события (часть 3) Готовимся к ЕГЭ
Готовимся к ЕГЭ Теория вероятностей
Теория вероятностей Свойства степеней
Свойства степеней Повторение 1 класс
Повторение 1 класс Кенгуру – математика для всех
Кенгуру – математика для всех Таблица умножения на 2
Таблица умножения на 2 Косинус угла
Косинус угла Презентация по математике "Решение задач. Закрепление" -
Презентация по математике "Решение задач. Закрепление" -  Финансовая математика: банки, вклады, кредиты. Часть 2
Финансовая математика: банки, вклады, кредиты. Часть 2 Системы булевых функций. Лекция 5
Системы булевых функций. Лекция 5 Простейшие линейные цепи при гармоническом воздействии
Простейшие линейные цепи при гармоническом воздействии Математический калейдоскоп. Игра
Математический калейдоскоп. Игра Проценты
Проценты Дифференциальные уравнения
Дифференциальные уравнения Вариационный ряд. Группировка данных при качественной и количественной вариациях
Вариационный ряд. Группировка данных при качественной и количественной вариациях Геометрия. Заготовка
Геометрия. Заготовка Презентация на тему Скорость, время, расстояние
Презентация на тему Скорость, время, расстояние  Уравнения, системы уравнений. Задание №9
Уравнения, системы уравнений. Задание №9 Интеграл. Определенный интеграл. Свойства
Интеграл. Определенный интеграл. Свойства Показательная функция, ее свойства и график
Показательная функция, ее свойства и график Математическая индукция
Математическая индукция Математический кроссворд. Для учащихся 5-6 классов
Математический кроссворд. Для учащихся 5-6 классов Бинарные отношения
Бинарные отношения