Содержание
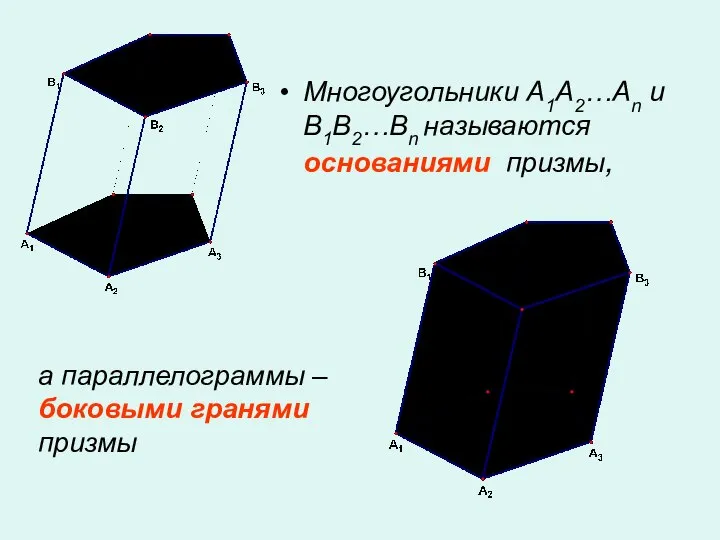
- 2. Многоугольники A1A2…An и B1B2…Bn называются основаниями призмы, а параллелограммы – боковыми гранями призмы
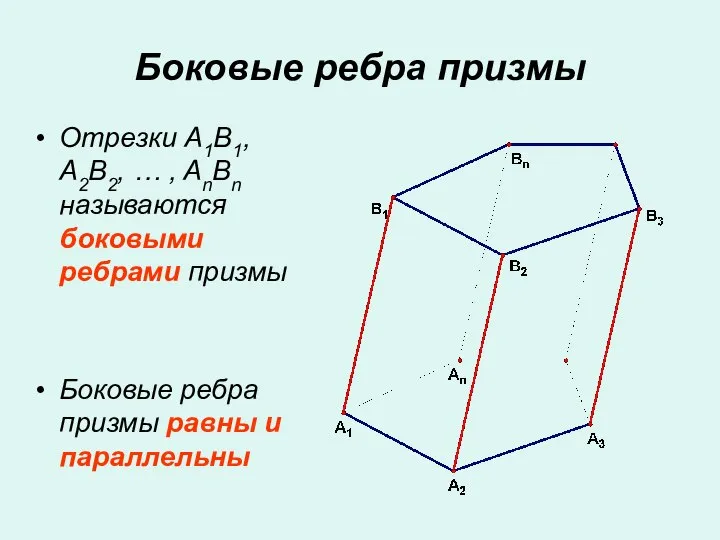
- 3. Отрезки A1B1, A2B2, … , AnBn называются боковыми ребрами призмы Боковые ребра призмы равны и параллельны
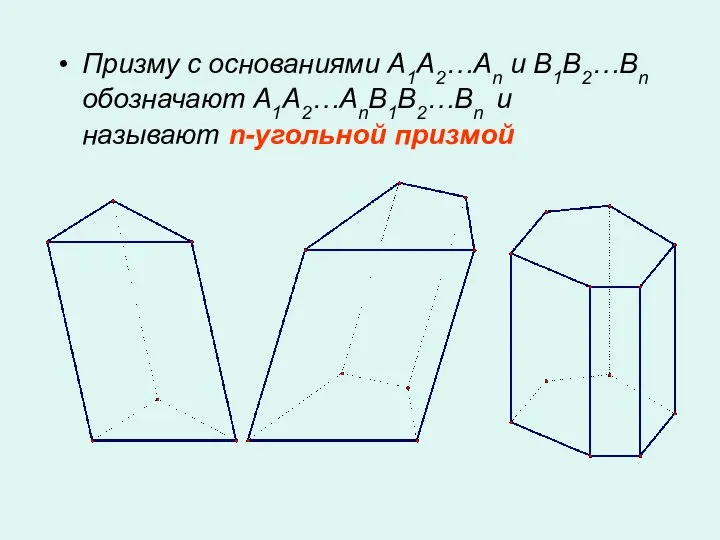
- 4. Призму с основаниями A1A2…An и B1B2…Bn обозначают A1A2…AnB1B2…Bn и называют n-угольной призмой
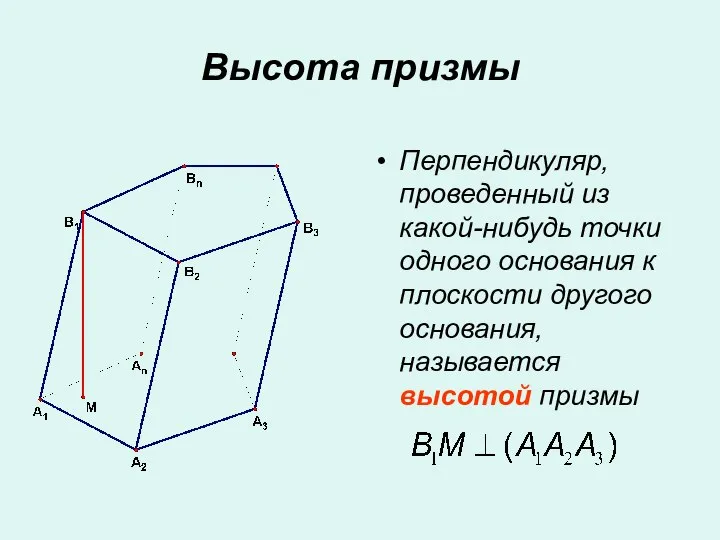
- 5. Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы Высота призмы
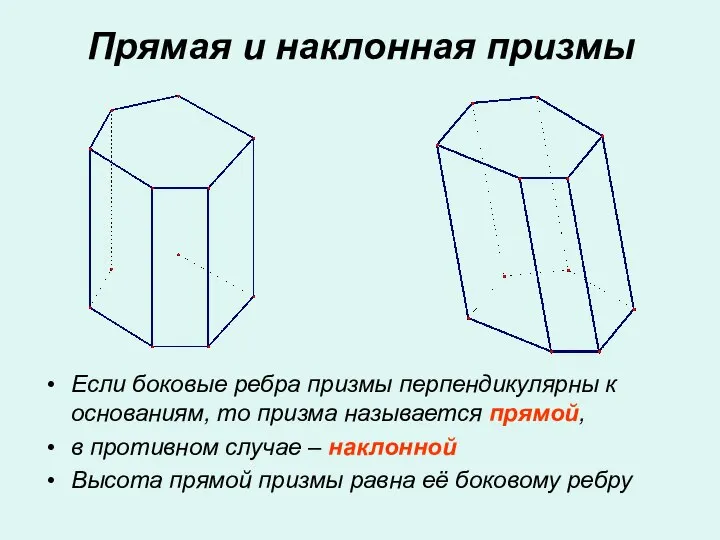
- 6. Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой, в противном случае – наклонной
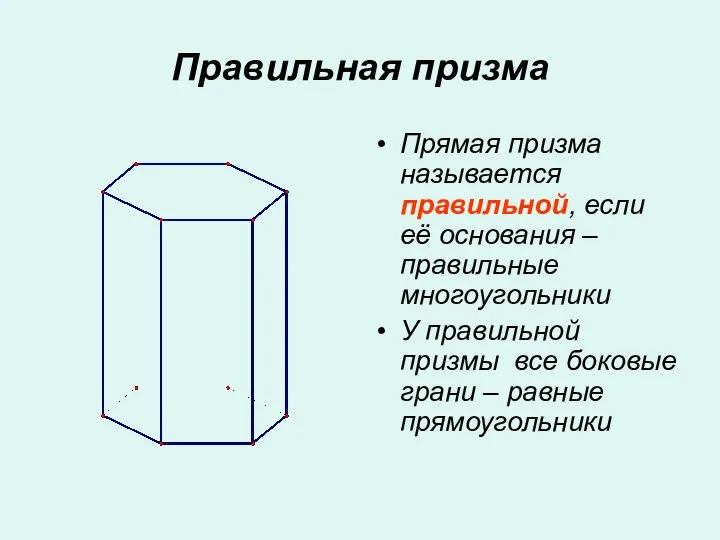
- 7. Правильная призма Прямая призма называется правильной, если её основания – правильные многоугольники У правильной призмы все
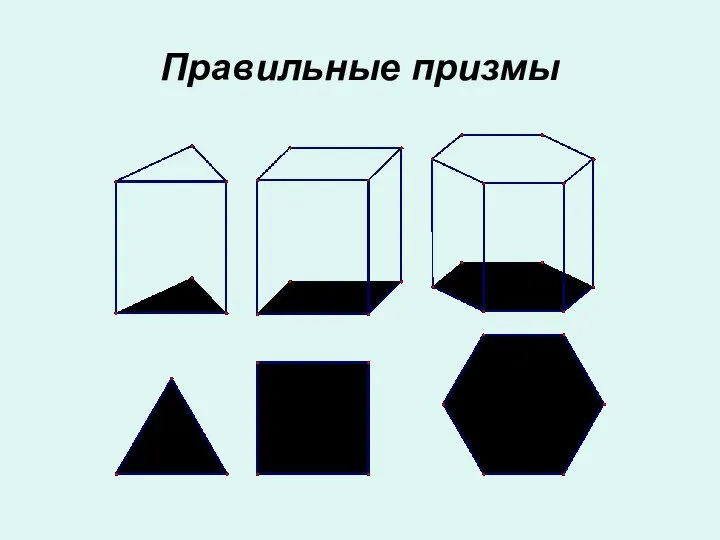
- 8. Правильные призмы
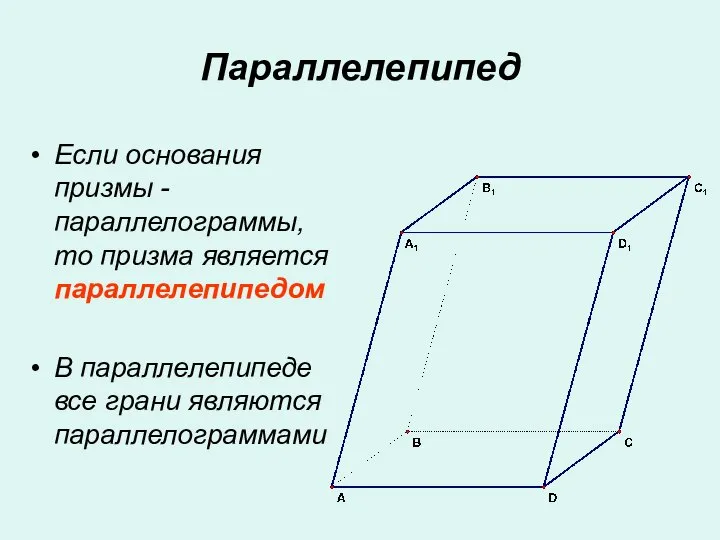
- 9. Параллелепипед Если основания призмы - параллелограммы, то призма является параллелепипедом В параллелепипеде все грани являются параллелограммами
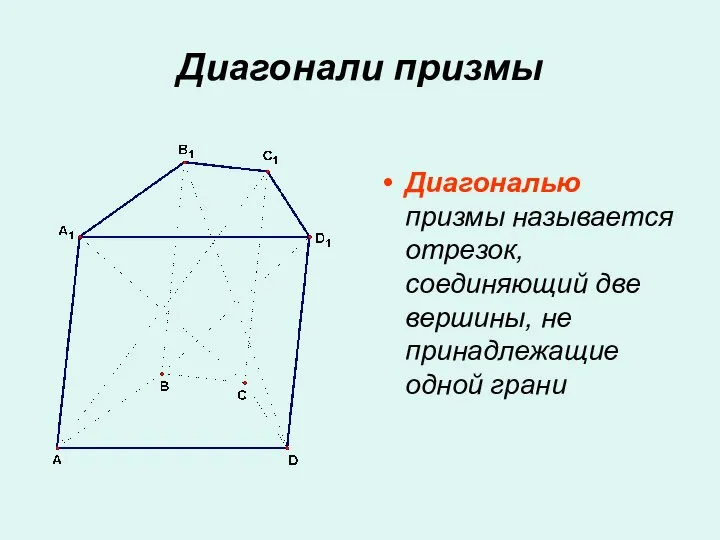
- 10. Диагонали призмы Диагональю призмы называется отрезок, соединяющий две вершины, не принадлежащие одной грани
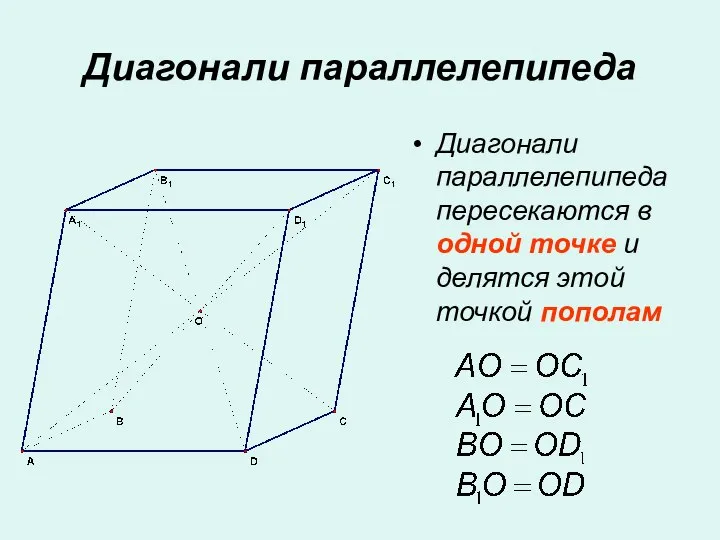
- 11. Диагонали параллелепипеда Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам
- 13. Скачать презентацию
 1 замечательный предел
1 замечательный предел Матрицы и действия над ними
Матрицы и действия над ними Элементы математической статистики
Элементы математической статистики Задачи на движение
Задачи на движение Параллельные прямые. Практическая работа
Параллельные прямые. Практическая работа Презентация на тему Линейная функция (7 класс)
Презентация на тему Линейная функция (7 класс)  Своя игра
Своя игра Сложение десятичных дробей
Сложение десятичных дробей Квадратичная функция и её график
Квадратичная функция и её график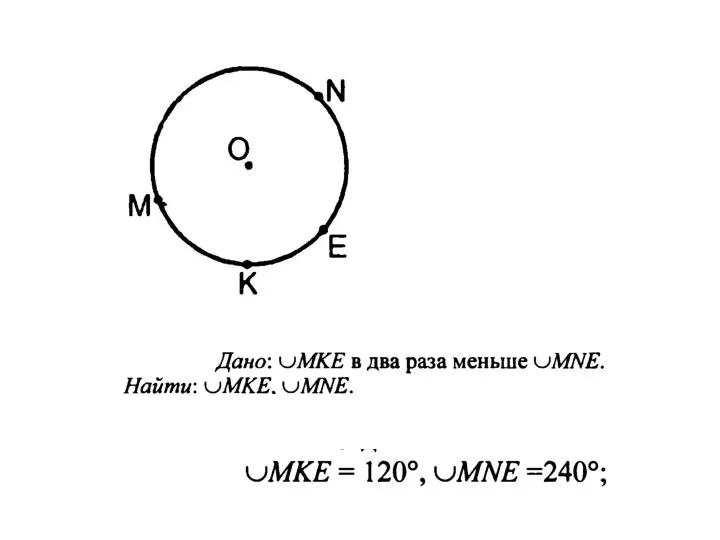 Теорема о вписанном угле
Теорема о вписанном угле Графики уравнений
Графики уравнений Множення числа на суму. Обчислення значень виразів на кілька дій. Урок №119
Множення числа на суму. Обчислення значень виразів на кілька дій. Урок №119 Лекция №5. Основные понятия теории вероятностей и математической статистики
Лекция №5. Основные понятия теории вероятностей и математической статистики Геометрические фигуры вокруг нас
Геометрические фигуры вокруг нас Четырехугольники. 2 урок
Четырехугольники. 2 урок МатШах(0.1)
МатШах(0.1) Контрольная работа. Умножение и деление
Контрольная работа. Умножение и деление Почти все об углах
Почти все об углах Площадь параллелограмма. Задачи
Площадь параллелограмма. Задачи История введения понятия функции в школьный курс математики и современность
История введения понятия функции в школьный курс математики и современность Методы решения логических задач
Методы решения логических задач Математические методы в психологии. Генеральная совокупность и выборка
Математические методы в психологии. Генеральная совокупность и выборка Уравнения! Реформа образования
Уравнения! Реформа образования Решение уравнений
Решение уравнений Математика. Треугольник
Математика. Треугольник обратные тригонометрические функции
обратные тригонометрические функции Теоремы косинусов и синусов
Теоремы косинусов и синусов Исследование функции с помощью производной и построение графика функции
Исследование функции с помощью производной и построение графика функции