Слайд 2Содержание
Определение
История возникновения логарифмов
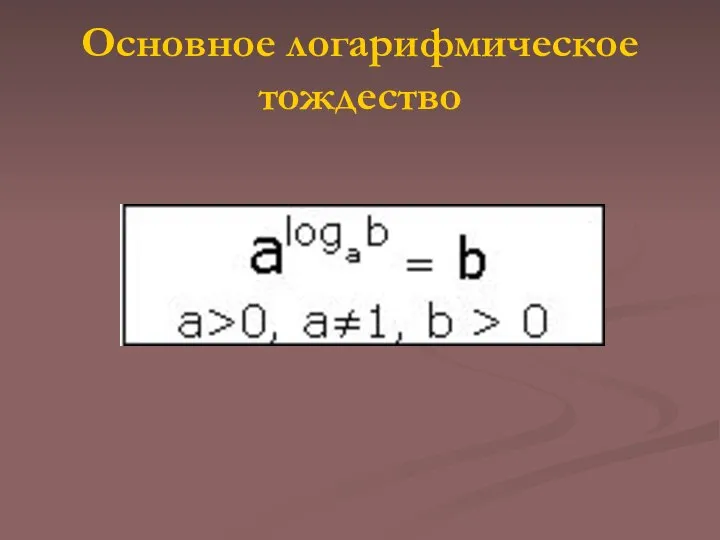
Основное логарифмическое тождество
Свойства логарифмов
Натуральные логарифмы

Десятичный логарифм
Формула перехода к новому основанию
Кологарифмы
Примеры
Слайд 3Определение:
Логарифмом положительного числа b по основанию называется показатель степени с, в которую

надо возвести число а, чтобы получить число b.
Слайд 4История возникновения логарифмов
Логарифмы были введены шотландским математиком Джоном Непером (1550-1617) и математиком

Иостом Бюрги (1552-1632
Бюрги пришел к логарифмам раньше, но опубликовал свои таблицы с опозданием (в 1620г.), а первой в 1614г. появилась работа Непера «Описание удивительной таблицы логарифмов».
Слайд 5Основное логарифмическое тождество
Слайд 7Натуральные логарифмы
Таблицы и свойства натуральных логарифмов аналогичны таблицам и свойствам обычных логарифмов.

Основное различие между теми и другими состоит в том, что целочисленная часть натурального логарифма не имеет существенного значения при определении положения десятичной запятой, и поэтому различие между мантиссой и характеристикой не играет особой роли.
Слайд 8Десятичный логарифм
lga = log10a

Слайд 9Формула перехода к новому основанию

Слайд 10Кологарифмы
Пропорциональные логарифмы при a = 1 называются кологарифмами и применяются в вычислениях,

когда приходится иметь дело с произведениями и частными. Кологарифм числа n равен логарифму обратного числа; т.е. cologn = log1/n = – logn. Если log2 = 0,3010, то colog2 = – 0,3010 = 0,6990 – 1. Преимущество использования кологарифмов состоит в том, что при вычислении значения логарифма выражений вида pq/r тройная сумма положительных десятичных долей logp + logq + cologr находится легче, чем смешанная сумма и разность logp + logq – logr.
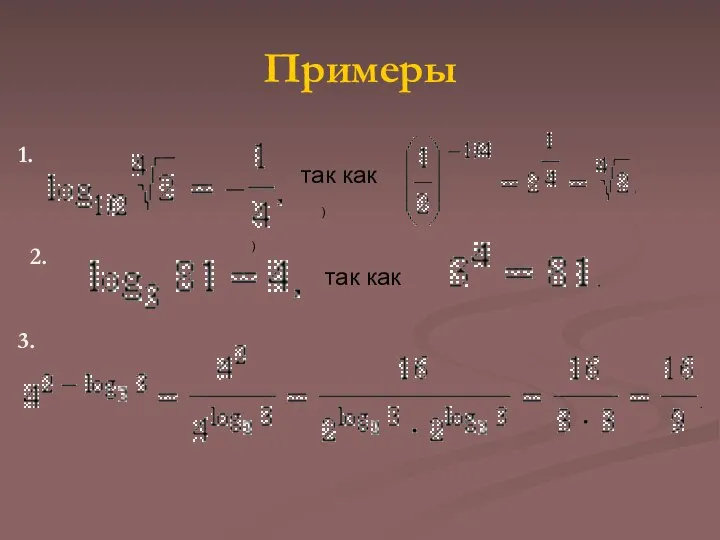
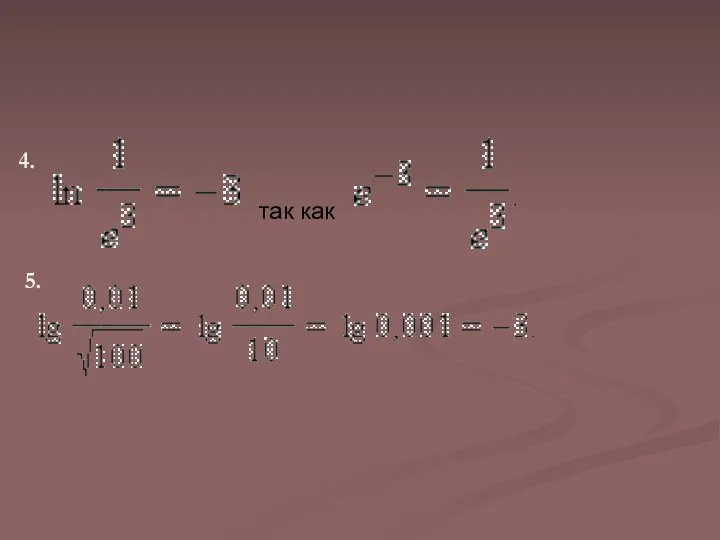
Слайд 11Примеры
)
так как
так как
)
1.
2.
3.











 Равнобедренный треугольник
Равнобедренный треугольник Математическое моделирование
Математическое моделирование Параллелограмм. Свойства. Признаки
Параллелограмм. Свойства. Признаки Презентация на тему Использование здоровьесберегающих технологий на уроках математики
Презентация на тему Использование здоровьесберегающих технологий на уроках математики  Элементы математической статистики
Элементы математической статистики Письменное умножение трёхзначного числа на однозначное
Письменное умножение трёхзначного числа на однозначное Matematika_5_klass_21_09_Chtenie_i_zapis_naturalnykh_chisel (1)
Matematika_5_klass_21_09_Chtenie_i_zapis_naturalnykh_chisel (1) Осевая и центральная симметрии
Осевая и центральная симметрии Геометрическая прогрессия
Геометрическая прогрессия Нумерация. Подготовка к ВПР
Нумерация. Подготовка к ВПР Теория множеств
Теория множеств Великие математики древности. Архимед, Пифагор, Евклид, Фалес
Великие математики древности. Архимед, Пифагор, Евклид, Фалес Деление дробей. Путешествие в Китай
Деление дробей. Путешествие в Китай Расстояние от точки до фигуры
Расстояние от точки до фигуры Однородные системы линейных алгебраических уравнений
Однородные системы линейных алгебраических уравнений Презентация на тему Теорема о сумме углов треугольника
Презентация на тему Теорема о сумме углов треугольника  Перехідна та імпульсна перехідна функції
Перехідна та імпульсна перехідна функції Решение уравнений, содержащих параметры
Решение уравнений, содержащих параметры Взаимное расположение двух окружностей
Взаимное расположение двух окружностей Презентация на тему Сравнение дробей (5 класс)
Презентация на тему Сравнение дробей (5 класс)  Случаи сложения и вычитания основанные на знаниях нумерации
Случаи сложения и вычитания основанные на знаниях нумерации Степень с натуральным показателем. Применение свойств к построению графиков степенных функций. 7 класс
Степень с натуральным показателем. Применение свойств к построению графиков степенных функций. 7 класс Методика изучения длины в процессе изучения геометрического материала
Методика изучения длины в процессе изучения геометрического материала Формула полной вероятности и формула Байеса
Формула полной вероятности и формула Байеса Арккосинус а. Решение уравнений
Арккосинус а. Решение уравнений Дифференциальное исчисление функции одной переменной
Дифференциальное исчисление функции одной переменной Задачи с параметрами.Расположение корней квадратного трёхчлена
Задачи с параметрами.Расположение корней квадратного трёхчлена