Признак параллелограма

Признак параллелограмма
Теорема 2. (Второй признак параллелограмма.) Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник - параллелограмм.

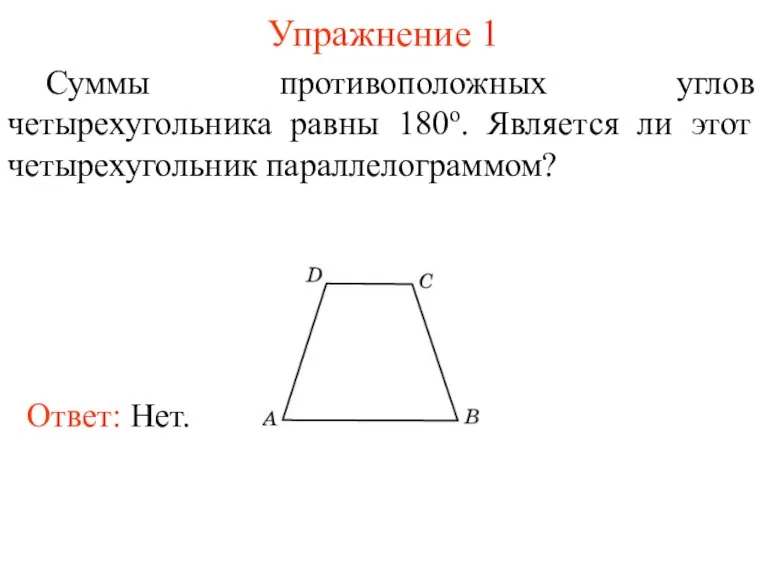
Упражнение 1
Суммы противоположных углов четырехугольника равны 180о. Является ли этот четырехугольник параллелограммом?

Упражнение 2
Все углы четырехугольника равны. Является ли этот четырехугольник параллелограммом?
Ответ: Да.

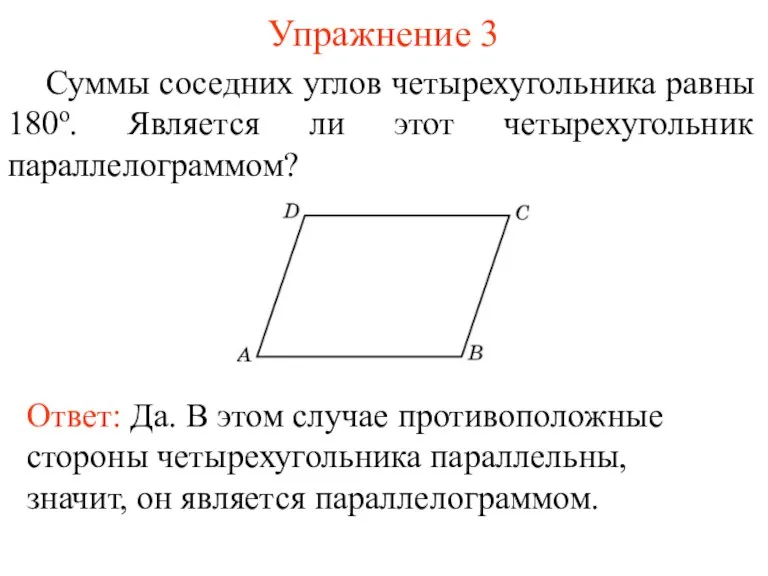
Упражнение 3
Суммы соседних углов четырехугольника равны 180о. Является ли этот четырехугольник параллелограммом?
Ответ: Да. В этом случае противоположные стороны четырехугольника параллельны, значит, он является параллелограммом.

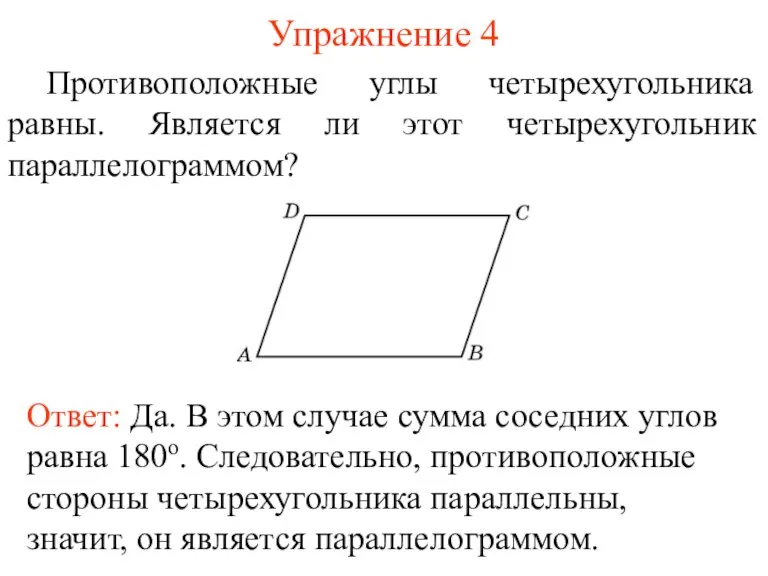
Упражнение 4
Противоположные углы четырехугольника равны. Является ли этот четырехугольник параллелограммом?
Ответ: Да. В этом случае сумма соседних углов равна 180о. Следовательно, противоположные стороны четырехугольника параллельны, значит, он является параллелограммом.

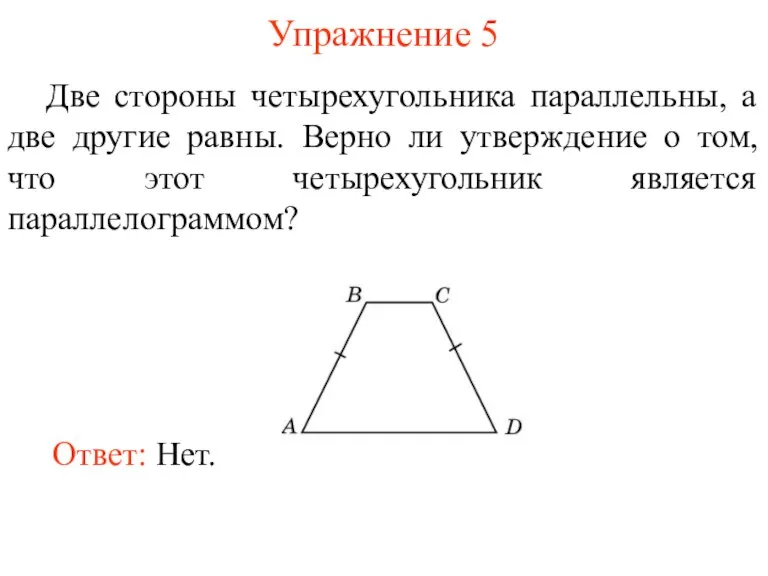
Упражнение 5
Две стороны четырехугольника параллельны, а две другие равны. Верно ли утверждение о том, что этот четырехугольник является параллелограммом?

Упражнение 6
В четырехугольнике ABCD AB = AD и BC = CD. Является ли этот четырехугольник параллелограммом?

Упражнение 7
Все стороны четырехугольника равны. Является ли этот четырехугольник параллелограммом?
Ответ: Да.

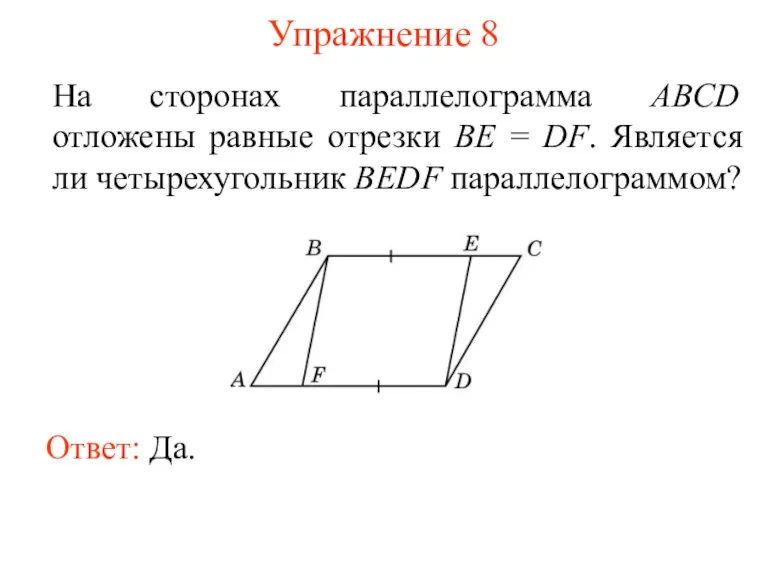
Упражнение 8
На сторонах параллелограмма ABCD отложены равные отрезки BE = DF. Является ли четырехугольник BEDF параллелограммом?
Ответ: Да.

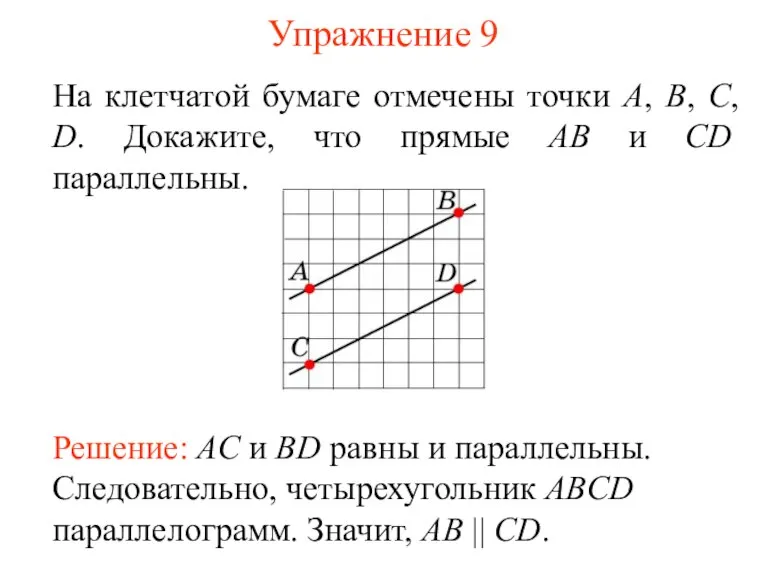
Упражнение 9
На клетчатой бумаге отмечены точки А, В, С, D. Докажите, что прямые АВ и CD параллельны.
Решение: AC и BD равны и параллельны. Следовательно, четырехугольник ABCD параллелограмм. Значит, AB || CD.

Упражнение 10
Из данной точки к окружности радиуса R проведены две взаимно перпендикулярные касательные. Чему равны отрезки этих касательных, заключенных между данной точкой и точками касания?
Ответ: R.

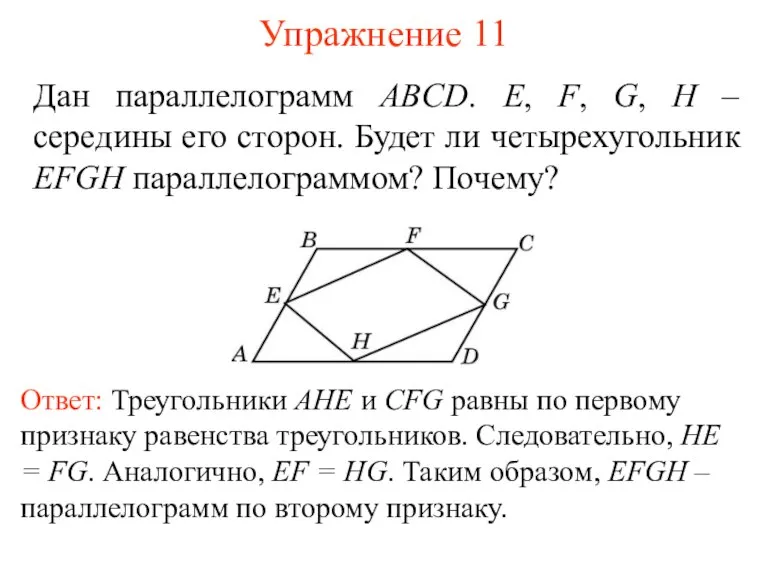
Упражнение 11
Дан параллелограмм ABCD. E, F, G, H – середины его сторон. Будет ли четырехугольник EFGH параллелограммом? Почему?
Ответ: Треугольники AHE и CFG равны по первому признаку равенства треугольников. Следовательно, HE = FG. Аналогично, EF = HG. Таким образом, EFGH – параллелограмм по второму признаку.

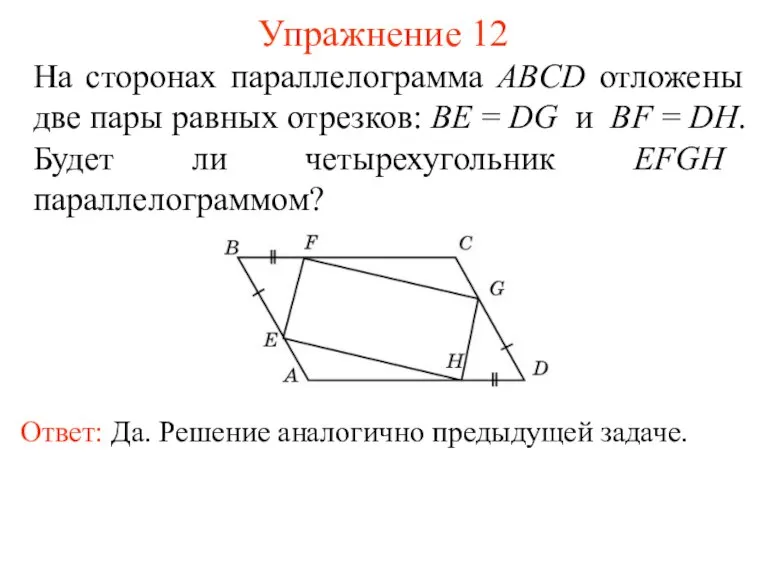
Упражнение 12
На сторонах параллелограмма ABCD отложены две пары равных отрезков: BE = DG и BF = DH. Будет ли четырехугольник EFGH параллелограммом?
Ответ: Да. Решение аналогично предыдущей задаче.

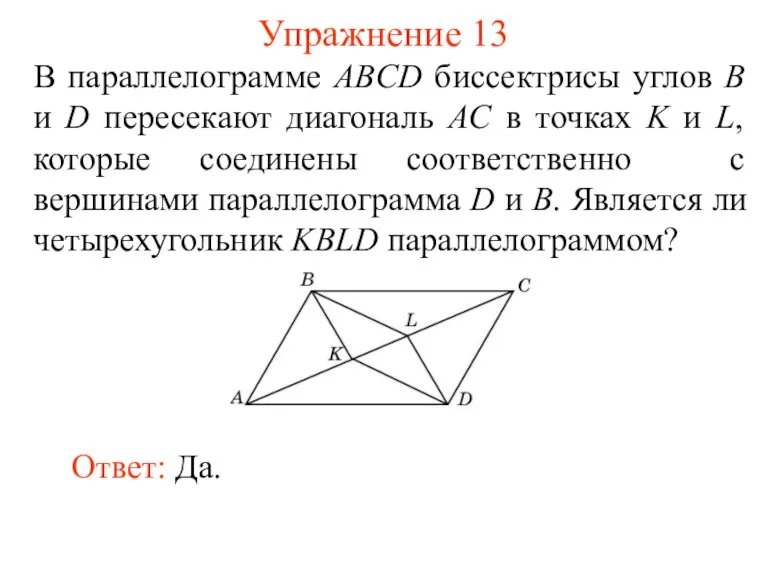
Упражнение 13
В параллелограмме ABCD биссектрисы углов B и D пересекают диагональ AC в точках K и L, которые соединены соответственно с вершинами параллелограмма D и B. Является ли четырехугольник KBLD параллелограммом?
Ответ: Да.

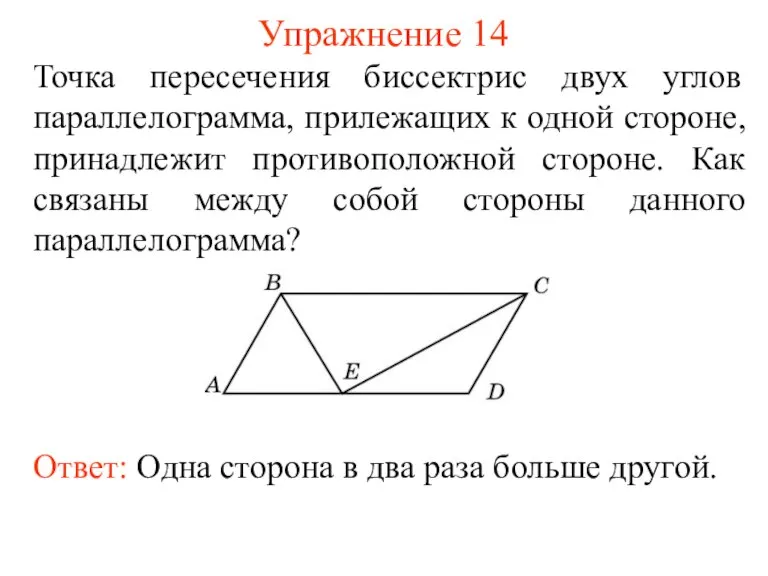
Упражнение 14
Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Как связаны между собой стороны данного параллелограмма?
Ответ: Одна сторона в два раза больше другой.

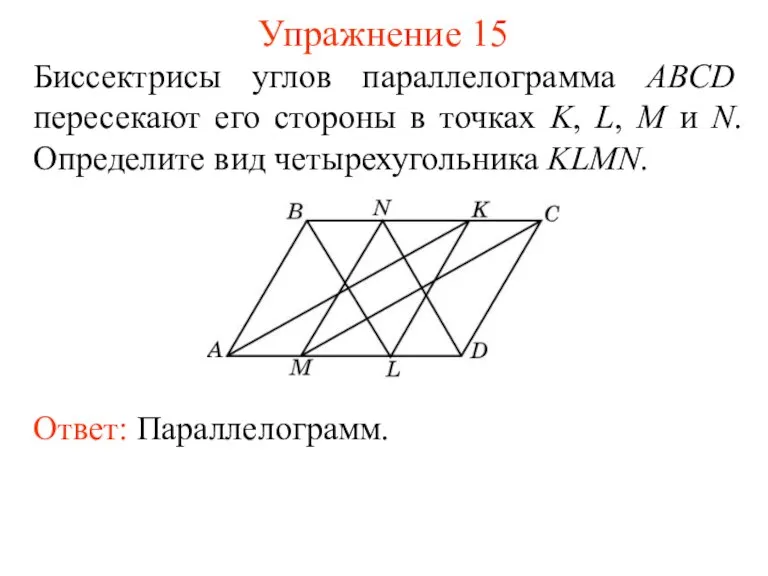
Упражнение 15
Биссектрисы углов параллелограмма ABCD пересекают его стороны в точках K, L, M и N. Определите вид четырехугольника KLMN.
Ответ: Параллелограмм.