Содержание
- 2. Актуализация знаний Что такое вектор Какой вектор называется коллинеарный Какой вектор называется нулевой
- 4. Скорость Путь Время Масса Перемещение Температура Ускорение Распредели физические величины в таблице.
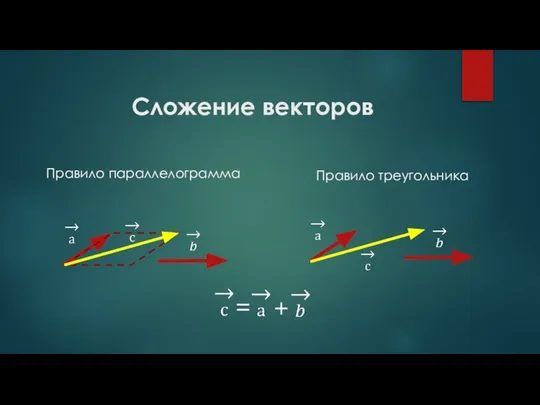
- 5. Сложение векторов Правило параллелограмма Правило треугольника = +
- 6. Тело из точки 1 переместилось вправо на расстояние 3 м в точку 2, а затем переместилось
- 7. 4. Точка совершила один полный оборот по окружности радиуса 50 см. Найти путь и перемещение. s
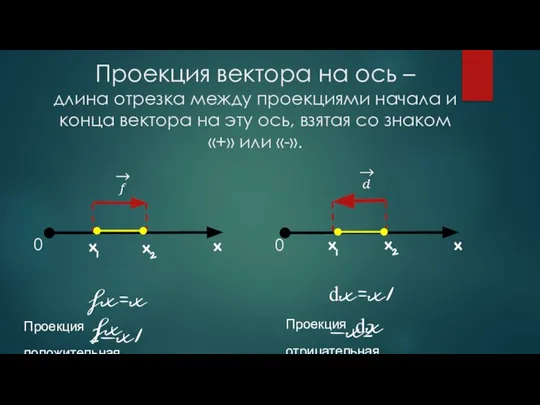
- 8. Проекция вектора на ось – длина отрезка между проекциями начала и конца вектора на эту ось,
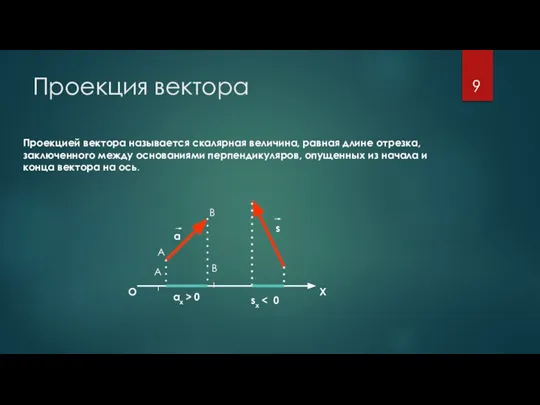
- 9. Проекция вектора Проекцией вектора называется скалярная величина, равная длине отрезка, заключенного между основаниями перпендикуляров, опущенных из
- 10. Если направление вектора не совпадает с направлением оси координат, то проекция этого вектора отрицательная Если вектор
- 11. Вычисление модуля вектора по его проекциям y 0 x x1 x2 y1 y2 vx vy
- 12. = +
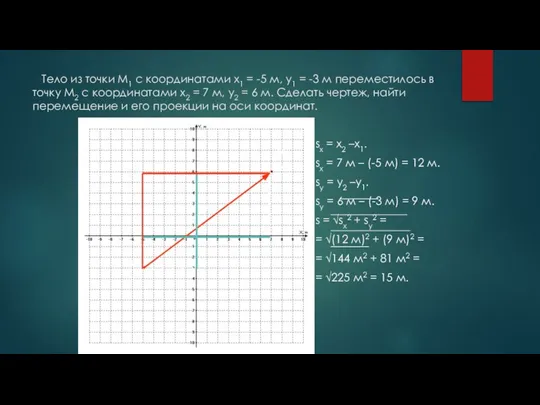
- 13. Тело из точки М1 с координатами x1 = -5 м, y1 = -3 м переместилось в
- 15. Скачать презентацию








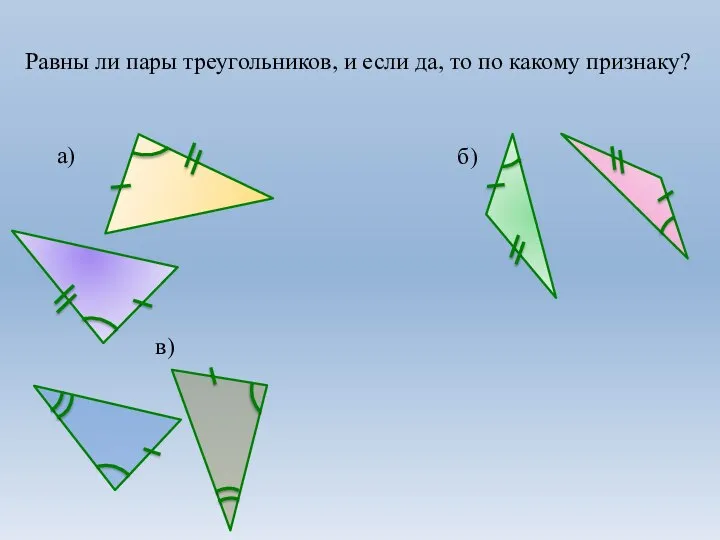 Второй признак равенства треугольников. 7 класс
Второй признак равенства треугольников. 7 класс Показательные функции
Показательные функции Решение задач с помощью составления систем уравнений. 9 класс
Решение задач с помощью составления систем уравнений. 9 класс Дискретная математика: теория алгоритмов и сложность вычислений
Дискретная математика: теория алгоритмов и сложность вычислений Основы логики
Основы логики Бином Ньютона
Бином Ньютона Решение задач на движение в противоположных направлениях
Решение задач на движение в противоположных направлениях Теория вероятностей, подготовка к ЕГЭ - 2019
Теория вероятностей, подготовка к ЕГЭ - 2019 Произведение событий. Условная вероятность. Теорема умножения вероятностей
Произведение событий. Условная вероятность. Теорема умножения вероятностей Prezentatsia_k_uroku_matematiki_v_6_kl
Prezentatsia_k_uroku_matematiki_v_6_kl Параллелограмм и трапеция. Урок 3
Параллелограмм и трапеция. Урок 3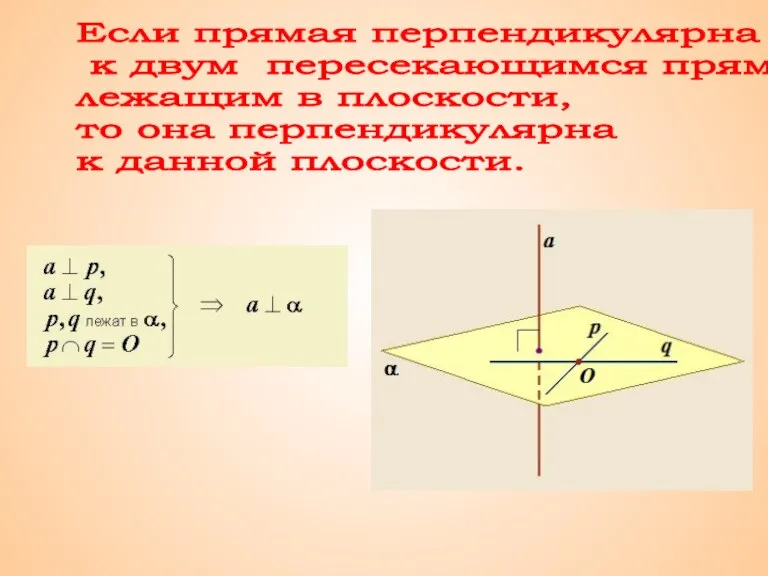 Признак перпендикулярности прямой и плоскости
Признак перпендикулярности прямой и плоскости История дробей
История дробей Математический магазин
Математический магазин Тест по теме Цилиндр
Тест по теме Цилиндр Презентация на тему Площадь прямоугольника: практикум
Презентация на тему Площадь прямоугольника: практикум  Кластерный анализ. Лекция 8
Кластерный анализ. Лекция 8 Возникновение комбинаторной теории
Возникновение комбинаторной теории Числовое значение буквенного выражения (часть 2)
Числовое значение буквенного выражения (часть 2) Презентация на тему Линейная функция 6 класс
Презентация на тему Линейная функция 6 класс  Игра-тренажер А знаете ли вы…. Математика 3 класс
Игра-тренажер А знаете ли вы…. Математика 3 класс Связь между суммой и слагаемыми (1 класс)
Связь между суммой и слагаемыми (1 класс) Параллельные прямые
Параллельные прямые Числа и точки на прямой. 5 класс
Числа и точки на прямой. 5 класс Funksiya. Funksiyaning berilish usullari
Funksiya. Funksiyaning berilish usullari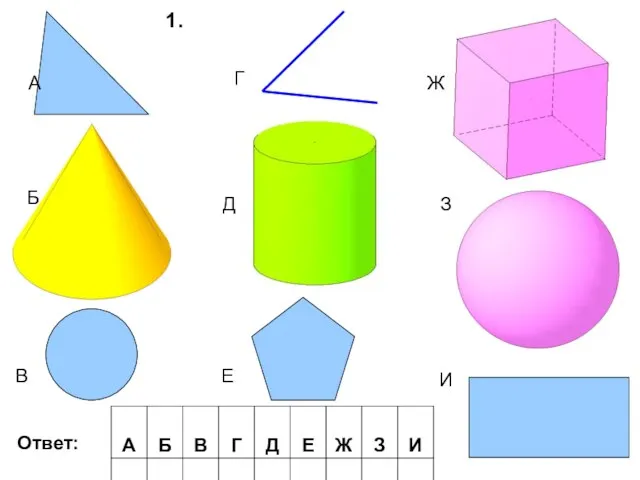 Геометрические тела. 5 класс
Геометрические тела. 5 класс Тригонометрические уравнения
Тригонометрические уравнения Решение задач по теме Параллельность прямой и плоскости
Решение задач по теме Параллельность прямой и плоскости