Статистика, вероятность, помеха, точность

Области применения ЦОС

Смежные области знаний

СТАТИСТИКА, ВЕРОЯТНОСТЬ, ПОМЕХА, ТОЧНОСТЬ
Тема №2

Понятие сигнал в ЦОС
Сигнал есть описание зависимости одного параметра от другого..
Непрерывные и дискретные сигналы.

Средняя величина и стандартное отклонение
Вычисление среднего значения.
Сигнал содержится в величинах от x0 до xN-1. Индекс i проходит через все эти величины, μ есть средняя величина.
ФОРМУЛА 2-2
Вычисление стандартного отклонения сигнала. Сигнал хранится в xi; μ есть среднее значение, найденное по формуле 2-1; N – число отсчетов;
σ - стандартное отклонение.

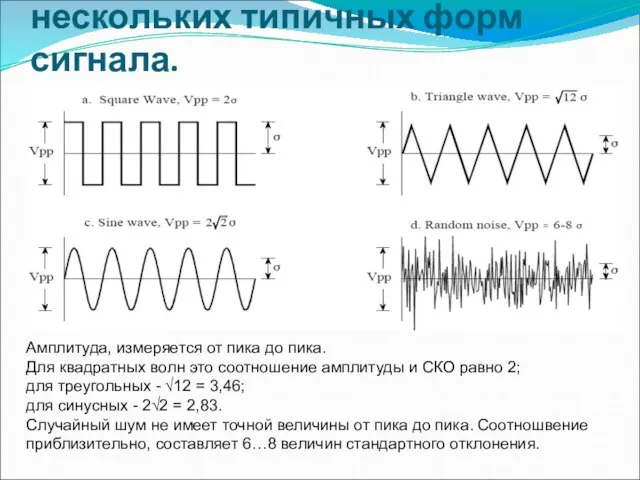
Стандартное отклонение для нескольких типичных форм сигнала.
Амплитуда, измеряется от пика до пика.
Для квадратных волн это соотношение амплитуды и СКО равно 2;
для треугольных - √12 = 3,46;
для синусных - 2√2 = 2,83.
Случайный шум не имеет точной величины от пика до пика. Соотношвение приблизительно, составляет 6…8 величин стандартного отклонения.

Программа для расчета среднего значения и стандартного отклонения

Расчет стандартного отклонения для динамической статистики

Взаимосвязь сигнала и порождающего его физического процесса

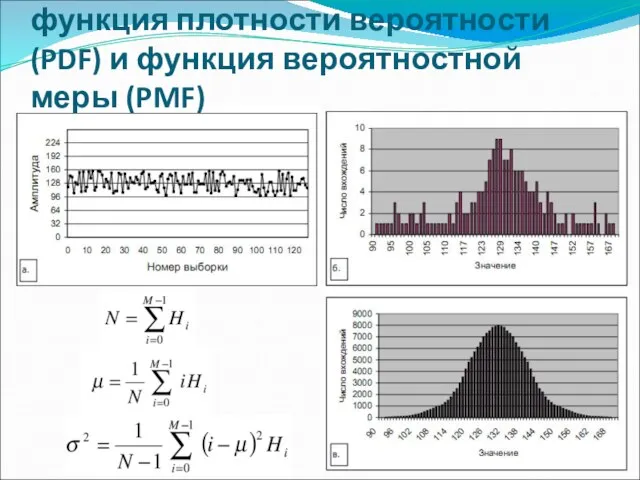
Гистограмма,
функция плотности вероятности (PDF) и функция вероятностной меры (PMF)

Расчета гистограммы, среднего значения и стандартного отклонения

Расчета гистограммы, среднего значения и стандартного отклонения

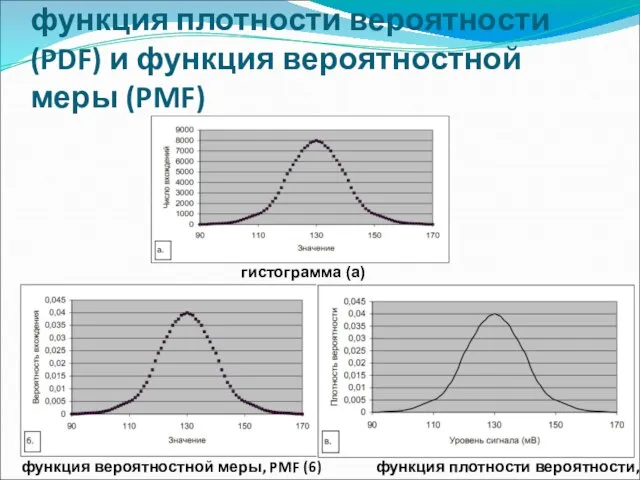
Гистограмма,
функция плотности вероятности (PDF) и функция вероятностной меры (PMF)
функция вероятностной меры, PMF (6) функция плотности вероятности, PDF (в)
гистограмма (а)

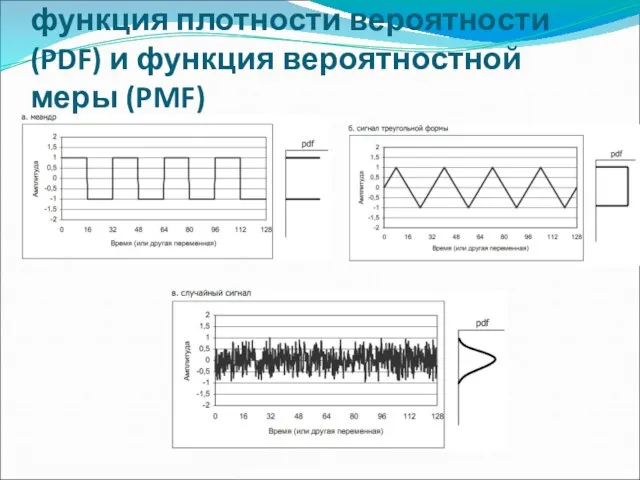
Гистограмма,
функция плотности вероятности (PDF) и функция вероятностной меры (PMF)

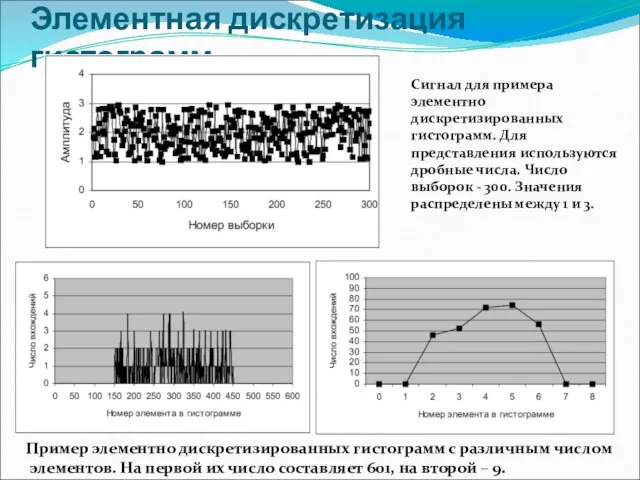
Элементная дискретизация гистограмм
Сигнал для примера элементно дискретизированных гистограмм. Для представления используются дробные числа. Число выборок - 300. Значения распределены между 1 и 3.
Пример элементно дискретизированных гистограмм с различным числом
элементов. На первой их число составляет 601, на второй – 9.

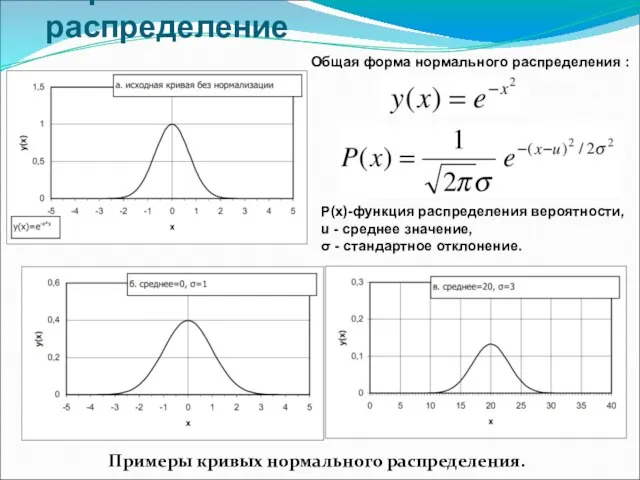
Нормальное распределение
Примеры кривых нормального распределения.
Общая форма нормального распределения :
Р(х)-функция распределения вероятности,
u - среднее значение,
σ - стандартное отклонение.

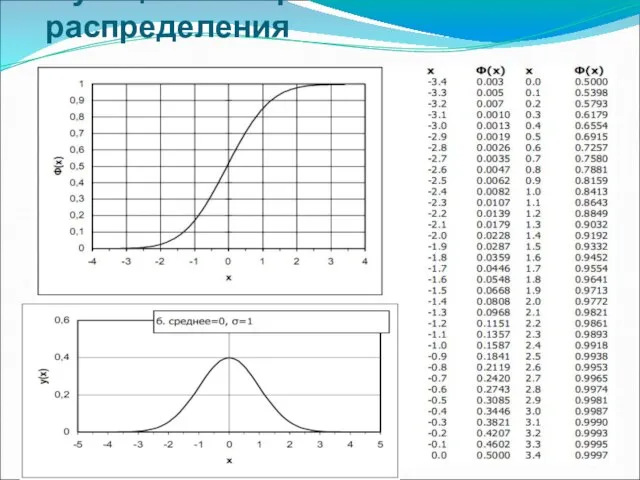
Функция интегрального распределения

Цифровая генерация помех
Способ генерации случайных сигналов с нормальным распределением
Генератор случайных чисел с нормальным распределением, средним значением 0 и стандартным отклонением 1.
R1 и R2 – случайные числа с равномерным распределением между 0 и 1.
Log по основанию e, cos в радианах.
Типичный алгоритм генерации равномерно распределенных случайных чисел между 0 и 1. S – исходное число; R – новое случайное число; a, b, c – соответствующим образом выбранные коэффициенты. Величина aS+b делится на c, и остаток запоминается как R.
R = (aS + b) mod c

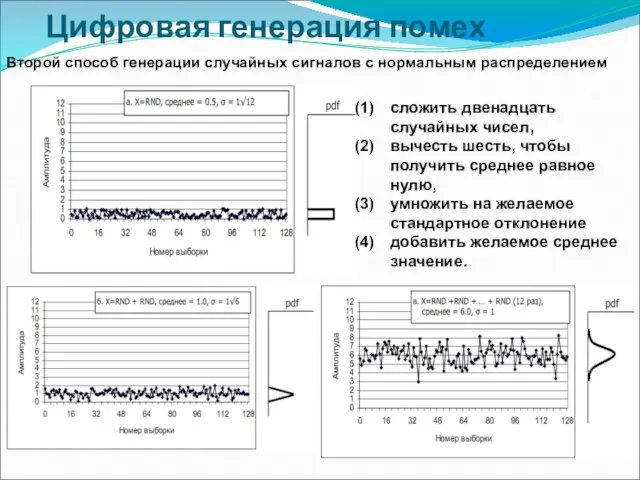
Цифровая генерация помех
Второй способ генерации случайных сигналов с нормальным распределением
сложить двенадцать случайных чисел,
вычесть шесть, чтобы получить среднее равное нулю,
умножить на желаемое стандартное отклонение
добавить желаемое среднее значение.