Содержание
- 2. определена Пример : в точке x = 0 не определена , но Предел функции Повтор лекции
- 3. Первый замечательный предел Рассмотрим окружность единичного радиуса, х - центральный угол, 0 Повтор лекции 2
- 4. . При этом , т.е. последовательность возрастает и она ограничена : . Повтор лекции 2
- 5. Повтор лекции 2
- 6. Повтор лекции 2
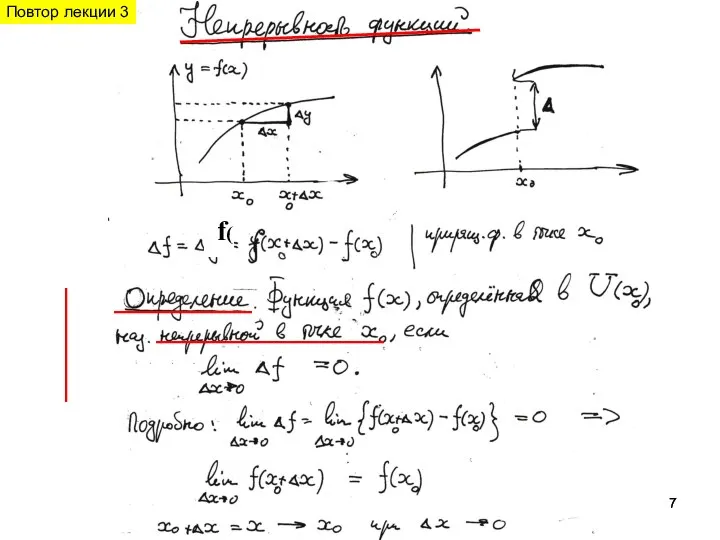
- 7. f( Повтор лекции 3
- 8. Непрерывные функции Рис.3 ≡≡≡≡≡≡≡≡≡≡≡≡≡≡≡≡≡≡≡≡ положительны. Поскольку Непрерывность функции f(x) в окрестности т. a сформулируем на языке
- 9. . 10 10 Повтор лекции 3 Повтор лекции 3
- 10. в точке Непрерывные функции Повтор лекции 3
- 11. 1 2 3 4 5 Повтор лекции 3
- 12. . Повтор лекции 3
- 13. Односторонние пределы. Повтор лекции 3
- 14. Продолжение. Если
- 15. Свойства непрерывных функций Рис. 9.6
- 16. .
- 17. ≡≡
- 18. .
- 20. Производная функции В
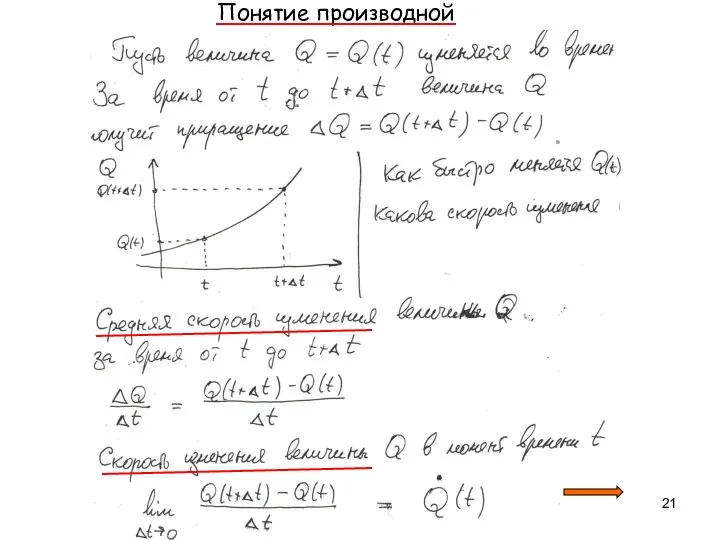
- 21. Понятие производной
- 22. . Таким образом, приходим к важнейшему понятию : Определение. Пусть ф. f(x) определена в окр. т.
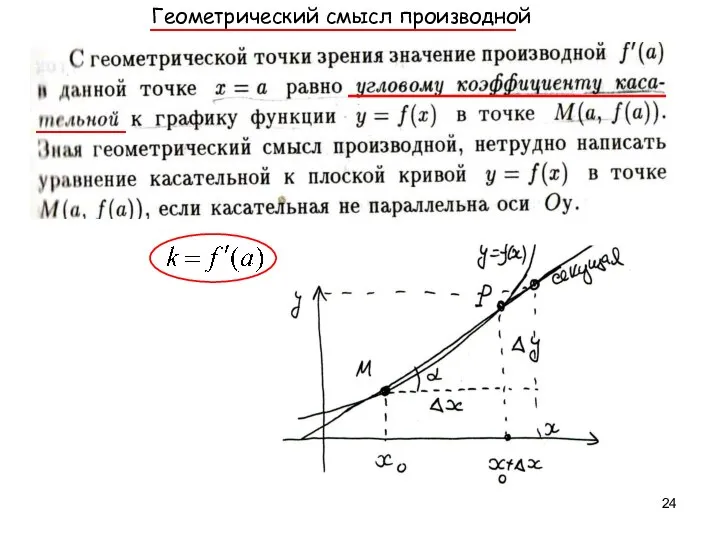
- 23. . ⎯⎯⎯⎯⎯⎯⎯ ⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯ ⎯⎯⎯ наз. предельное положение секущей при P M
- 24. Геометрический смысл производной
- 25. Уравнение нормали в точке Прямая, проходящая через точку М и перпендикулярная к касательной, наз. нормалью к
- 27. Дифференцируемость функций
- 30. Продолжение
- 31. ≡≡≡≡≡≡
- 34. Производные обратных элементарных функций
- 35. Продолжение
- 37. Спасибо за внимание
- 38. Десять открытий в физике океана А.С. Монин, Н.Н. Корчагин Прикладная математика и . открытия в Мировом
- 41. .
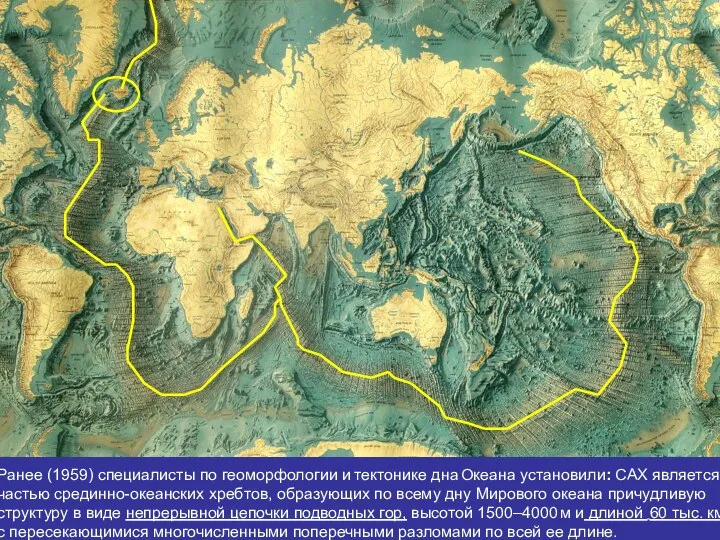
- 42. . . Ранее (1959) специалисты по геоморфологии и тектонике дна Океана установили: САХ является частью срединно-океанских
- 45. Скачать презентацию






































 Презентация по математике "Единицы длины. Метр" -
Презентация по математике "Единицы длины. Метр" -  Прибавление и вычитание числа 6
Прибавление и вычитание числа 6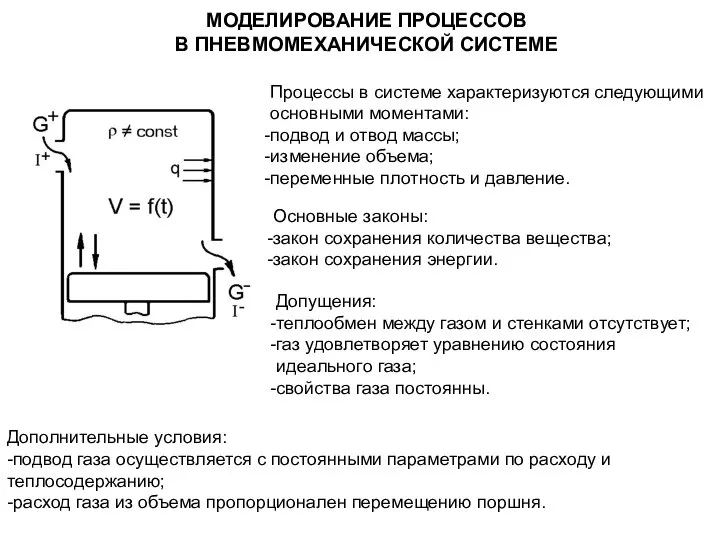 Моделирование процессов в пневмомеханической системе
Моделирование процессов в пневмомеханической системе Алгоритм принятия решения о выборе критерия оценки измерений
Алгоритм принятия решения о выборе критерия оценки измерений Переместительное свойство сложения
Переместительное свойство сложения Понятие формы. Многообразие форм окружающего мира
Понятие формы. Многообразие форм окружающего мира Подобие треугольников. Признаки
Подобие треугольников. Признаки Четырехугольники. Чертежи
Четырехугольники. Чертежи Итоговое повторение курса геометрии 8 класса
Итоговое повторение курса геометрии 8 класса Математика для анализа больших данных
Математика для анализа больших данных Стародубцева Анна 9-а класс
Стародубцева Анна 9-а класс Решение уравнений с переменной под знаком модуля
Решение уравнений с переменной под знаком модуля Деление с остатком. 4 класс
Деление с остатком. 4 класс Определители второго и третьего порядков
Определители второго и третьего порядков Возведение в квадрат суммы и разности двух выражений. Тест
Возведение в квадрат суммы и разности двух выражений. Тест Многранники в нашей жизни
Многранники в нашей жизни Построение сечений в многогранниках
Построение сечений в многогранниках Теория вероятностей. Действия над вероятностями
Теория вероятностей. Действия над вероятностями Площадь многоугольников
Площадь многоугольников Моделирование в среде МАTLAB
Моделирование в среде МАTLAB Статистика. Необходимость возникновения статистики-науки
Статистика. Необходимость возникновения статистики-науки Презентация на тему История возникновения интеграла
Презентация на тему История возникновения интеграла  Опорні конспекти на уроках математики
Опорні конспекти на уроках математики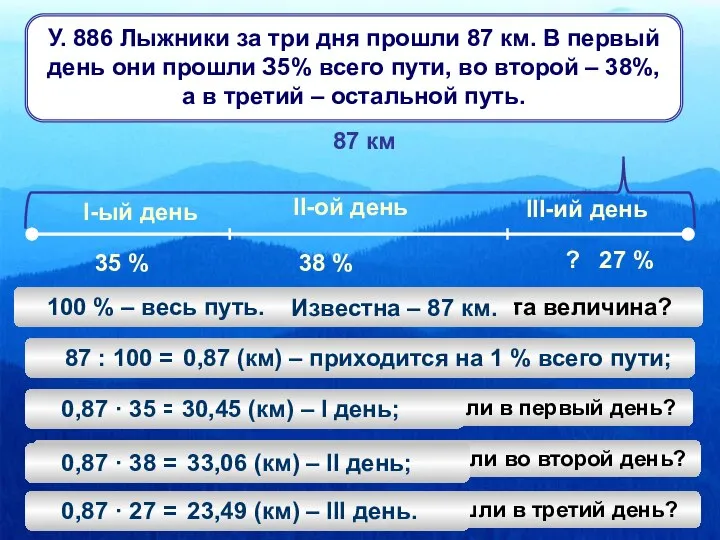 Задачи о лыжниках
Задачи о лыжниках Обратные тригонометрические функции, их графики и формулы
Обратные тригонометрические функции, их графики и формулы Collatz Conjecture
Collatz Conjecture Аксиомы стереометрии и следствия из них
Аксиомы стереометрии и следствия из них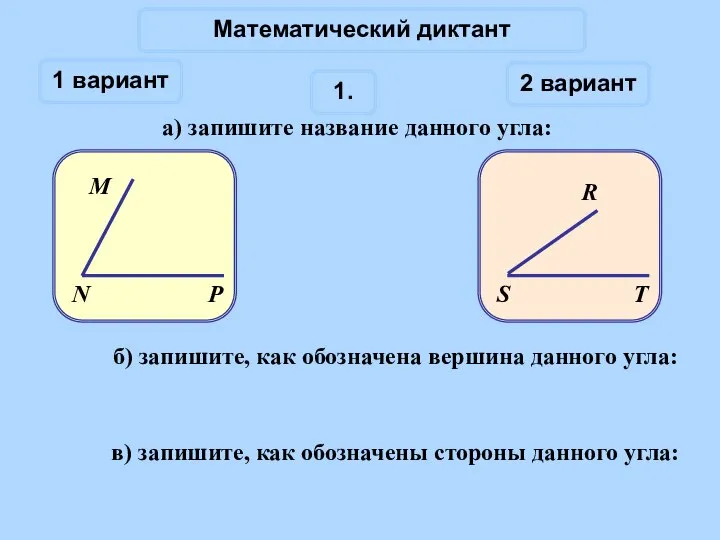 Углы. Математический диктант
Углы. Математический диктант