- Главная
- Математика
- Производная функция

Содержание
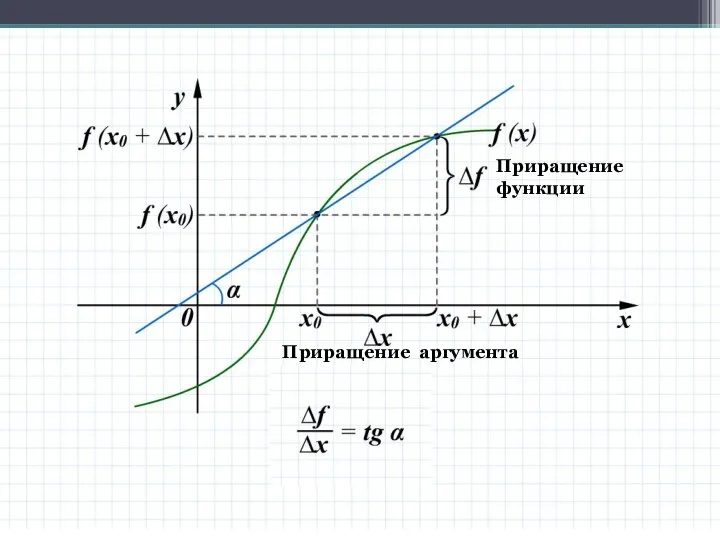
Слайд 3Приращение аргумента
Приращение функции
Приращение аргумента
Приращение функции
Слайд 12Механический смысл производной
Механический смысл производной

Слайд 14Задача 2:
Тело движется по закону:
?= 5 + 5t + 7t²
Чему равна
Задача 2:
Тело движется по закону:
?= 5 + 5t + 7t²
Чему равна

скорость тела через 5 секунд?
Задача 1:
Автомобиль, стартуя с места и двигаясь с постоянным ускорением, через 12 секунд достигает скорости 100 км/ч. Какое расстояние в метрах он пройдет за это время, если скорость и пройденный путь при равноускоренном движении с ускорением a определяется по формулам: ?(t)=? ̥+ at; s(t)=?t + ?
- Предыдущая
Цитостатики. Азатиоприн и 6-меркаптопуринСледующая -
Семейный бюджет






 Презентация на тему ТАБЛИЦА УМНОЖЕНИЯ
Презентация на тему ТАБЛИЦА УМНОЖЕНИЯ  Представление о замкнутой и незамкнутой линиях
Представление о замкнутой и незамкнутой линиях Показательные и логарифмические уравнения, системы, неравенства
Показательные и логарифмические уравнения, системы, неравенства Решение задач на временные отношения (подготовка к олимпиаде по математике обучающихся 4 класса)
Решение задач на временные отношения (подготовка к олимпиаде по математике обучающихся 4 класса) Иррациональные уравнения и их системы
Иррациональные уравнения и их системы Задачи по комбинаторике
Задачи по комбинаторике Функция одной переменной. Предел функции в точке и непрерывность функции. Точки разрыва. (Лекция 2)
Функция одной переменной. Предел функции в точке и непрерывность функции. Точки разрыва. (Лекция 2) Числовые последовательности
Числовые последовательности Презентация на тему РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ
Презентация на тему РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ  Многоугольник
Многоугольник Проценты в нашей жизни
Проценты в нашей жизни Логика предикатов. Лекция 8
Логика предикатов. Лекция 8 ВПР по математике. Тренировочные задания
ВПР по математике. Тренировочные задания Решение треугольников
Решение треугольников Площадь правильного треугольника
Площадь правильного треугольника Логика. Введение
Логика. Введение Рабочая программа внеурочной деятельности по математике для 5 класса Математическая мозаика
Рабочая программа внеурочной деятельности по математике для 5 класса Математическая мозаика Вписанi й описанi. Чотирикутники
Вписанi й описанi. Чотирикутники Найди соседей числа
Найди соседей числа Длина окружности
Длина окружности Многогранники. Основные понятия
Многогранники. Основные понятия Неопределенный интеграл. Способы вычисления
Неопределенный интеграл. Способы вычисления Векторы
Векторы Співвідношення між тригонометричними функціями
Співвідношення між тригонометричними функціями Асимптоты функции
Асимптоты функции Занятие 1. Вводное занятие
Занятие 1. Вводное занятие Разложение вектора по трём некомпланарным векторам
Разложение вектора по трём некомпланарным векторам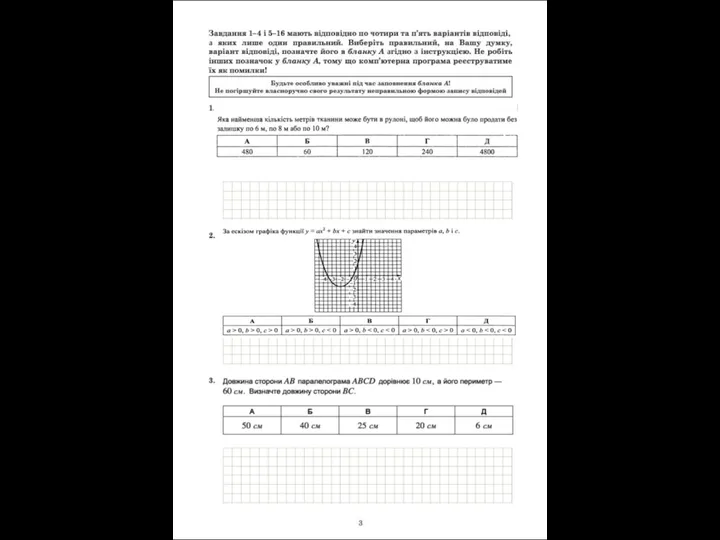 Задания для ЗНО
Задания для ЗНО