Содержание
- 5. Часть 2.Производная функции Определение производной Геометрический смысл производной Связь между непрерывностью и дифференцируемостью Производные основных элементарных
- 6. Live version
- 7. Live version
- 8. Определение производной Пусть функция y = f(x) определена в некотором интервале (a; b). Аргументу x придадим
- 9. Определение производной Итак, по определению: Функция y = f(x) , имеющая производную в каждой точке интервала
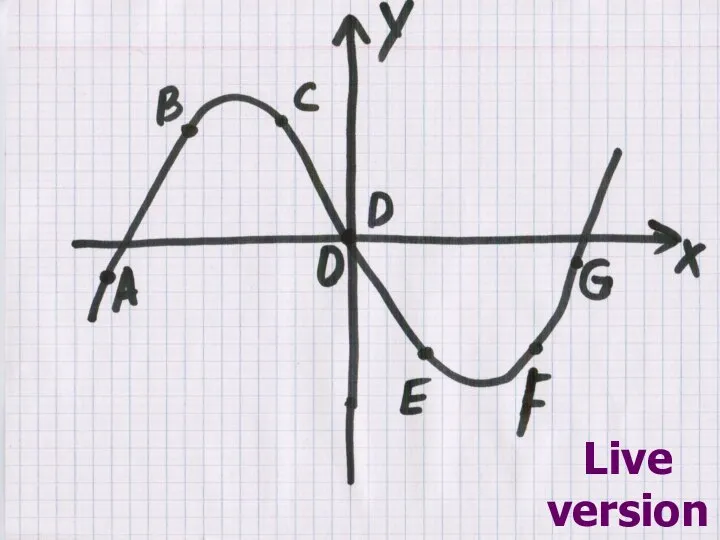
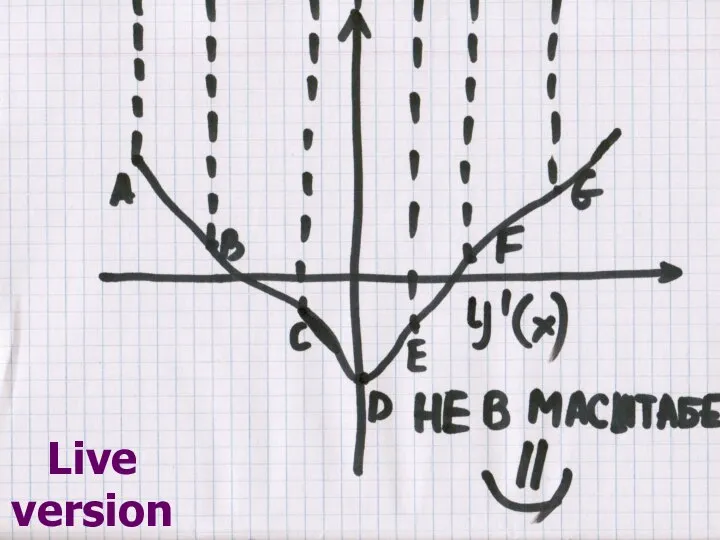
- 10. Геометрический смысл производной Возьмем на непрерывной кривой L две точки М и М1: х f(x )
- 11. Геометрический смысл производной Производная f ’(x) равна угловому коэффициенту касательной к графику функции y = f(x)
- 12. Связь между непрерывностью и дифференцируемостью функции Если функция f(x) дифференцируема в некоторой точке , то она
- 13. Производные основных элементарных функций
- 14. Правила дифференцирования Пусть u(x) , v(x) и w(x) – дифференцируемые в некотором интервале (a; b) функции,
- 15. Пример Вычислить производную функции
- 16. Пример Вычислить производную функции Данную функцию можно представить следующим образом: Коротко:
- 17. Производная неявно заданной функции Если функция задана уравнением y = f(х) , разрешенным относительно y, то
- 18. Производная функции, заданной параметрически
- 19. Логарифмическое дифференцирование В ряде случаев для нахождения производной целесообразно заданную функцию сначала прологарифмировать, а затем результат
- 21. Скачать презентацию
















 Десятичные дроби. Колесо истории
Десятичные дроби. Колесо истории Знаки сравнения и знак равенства
Знаки сравнения и знак равенства Прямые измерения, косвенные, совокупные и совместные
Прямые измерения, косвенные, совокупные и совместные Неравенства системы и совокупности неравенств
Неравенства системы и совокупности неравенств Решение типовой задачи
Решение типовой задачи Числа. Комплексные числа
Числа. Комплексные числа Анаграмма. Великолепная семерка
Анаграмма. Великолепная семерка Задачи с дробями
Задачи с дробями Подготовка к экзамену по математике
Подготовка к экзамену по математике Конус. Виды конусов. Конусы в нашей жизни
Конус. Виды конусов. Конусы в нашей жизни Решение нормальных систем обыкновенных дифференциальных уравнений (ОДУ)
Решение нормальных систем обыкновенных дифференциальных уравнений (ОДУ) История развития экономико-математических методов (ЭММ) и моделей. Лекция 1
История развития экономико-математических методов (ЭММ) и моделей. Лекция 1 Понятие интеграла
Понятие интеграла Уравнение плоскости
Уравнение плоскости Старинные меры длины на Руси
Старинные меры длины на Руси Волшебный треугольник
Волшебный треугольник Неравенства с двумя переменными
Неравенства с двумя переменными Определение предела последовательности
Определение предела последовательности Решение логарифмических уравнений
Решение логарифмических уравнений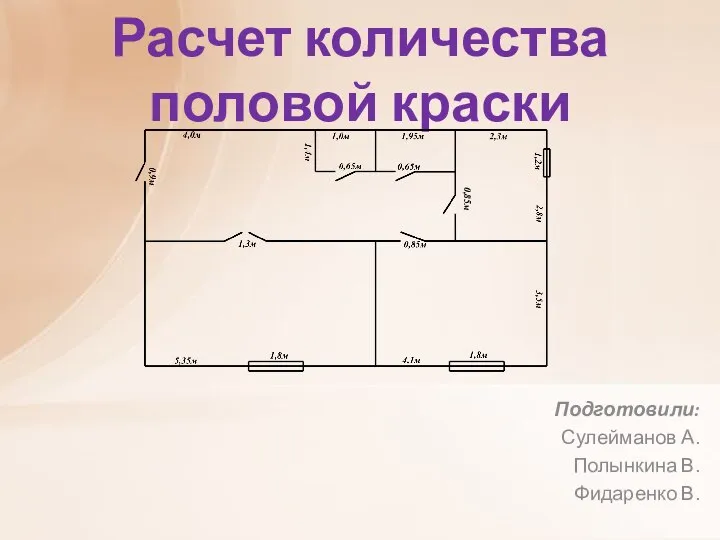 Расчет количества половой краски
Расчет количества половой краски Презентация на тему Наглядная геометрия для начальной школы
Презентация на тему Наглядная геометрия для начальной школы  Презентация на тему Сложение и вычитание круглых десятков и однозначных чисел
Презентация на тему Сложение и вычитание круглых десятков и однозначных чисел  Առարկա՝ Հյուսվածքները եւ դրանց մոդելները երկրաչափության դպրոցական դասընթացում (ընտրովի դասընթաց)
Առարկա՝ Հյուսվածքները եւ դրանց մոդելները երկրաչափության դպրոցական դասընթացում (ընտրովի դասընթաց) В мире чисел и цифр
В мире чисел и цифр Прямоугольный параллелепипед
Прямоугольный параллелепипед Сложение и вычитание натуральных чисел. Тренажер
Сложение и вычитание натуральных чисел. Тренажер Математическая карусель
Математическая карусель Занимательная математика (3 класс)
Занимательная математика (3 класс)