Свойства абсолютно регурярного графа

Введение
Абсолютно регулярным называется граф,
который может быть наложен сам на себя
так, чтобы любая выбранная вершина
совместилась с любой другой.
Цели:
- изучить свойства абсолютно регулярных графов;
- научиться находить абсолютно регулярные графы и использовать их свойства.

Теорема
Четыре параметра в srg(v,k,λ,μ) не являются независимыми
и должны удовлетворять следующему условию: (v-k-1)μ=k(k-λ-1)

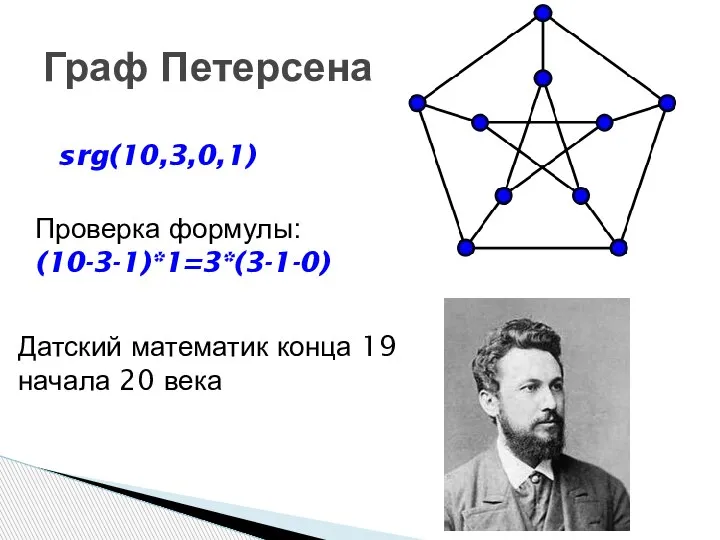
Граф Петерсена
srg(10,3,0,1)
Проверка формулы:
(10-3-1)*1=3*(3-1-0)
Датский математик конца 19
начала 20 века

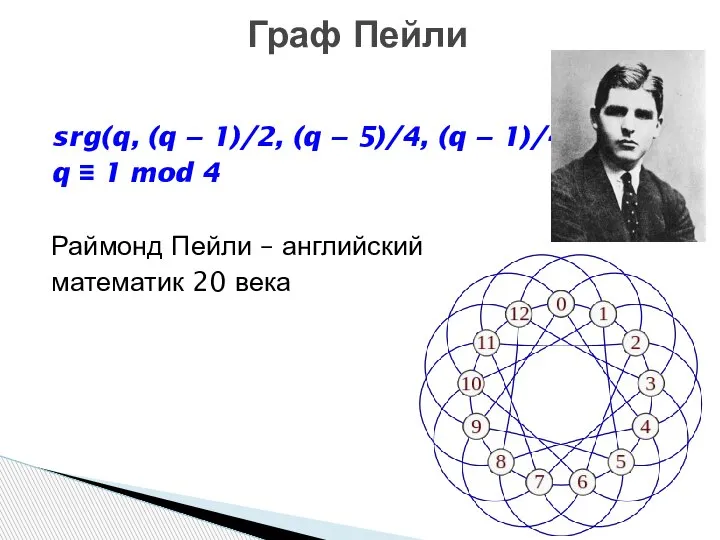
srg(q, (q − 1)/2, (q − 5)/4, (q − 1)/4)
q ≡ 1 mod 4
Раймонд Пейли – английский
математик 20 века
Граф Пейли

сильно регулярный граф с
параметрами srg(27, 16, 10, 8).
Граф Шлефли
Людвиг Шлефли – швейцарский
математик 19 века

n × n квадратный ладейный
граф является
абсолютно регулярным
с параметрами
srg(n2, 2n − 2, n − 2, 2)
Ладейный граф
В теории графов ладейным графом
называется граф, представляющий
все допустимые ходы ладьи
на прямоугольной доске.

Антиграф к абсолютно регулярному графу srg(v,k,λ,μ) тоже абсолютно регулярен. Это srg(v, v−k−1, v−2−2k+μ, v−2k+λ)
Любой полный граф тоже является абсолютно регулярным – это
srg(v,v−1,v−2,v−2)
Простой цикл длины 4 и 5 является абсолютно регулярным – это srg(4,2,0,2) и srg(5,2,0,1).
Факты

Абсолютно регулярный граф – красивая и
крайне любопытная математическая
структура, которая может быть изображена
на плоскости в виде симметричной и
завораживающей схемы.
Вывод