Содержание
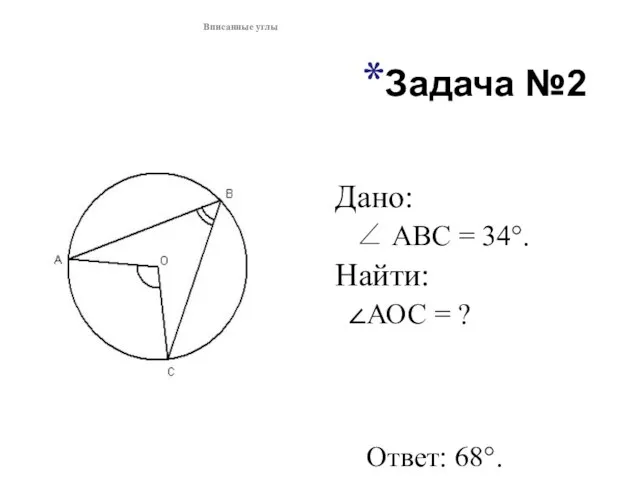
- 2. Задача №2 Дано: ∠ АВС = 34°. Найти: АОС = ? Ответ: 68°. Вписанные углы
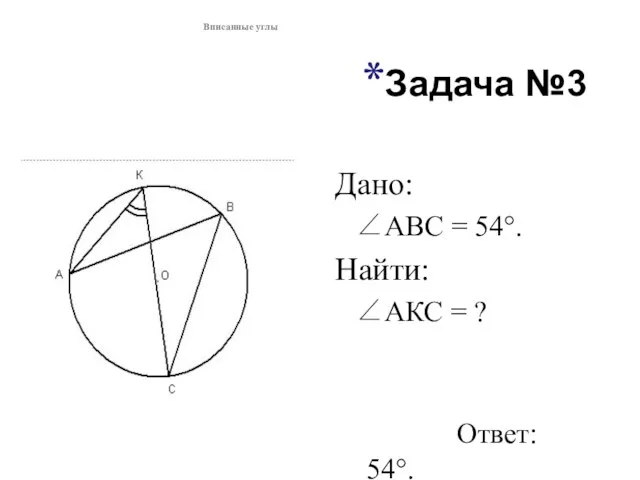
- 3. Задача №3 Дано: ∠АВС = 54°. Найти: ∠АКС = ? Ответ: 54°. Вписанные углы
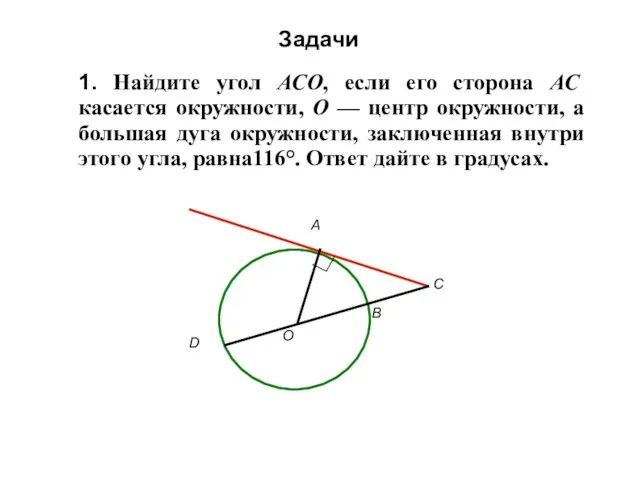
- 4. Задачи 1. Найдите угол АСО, если его сторона АС касается окружности, О — центр окружности, а
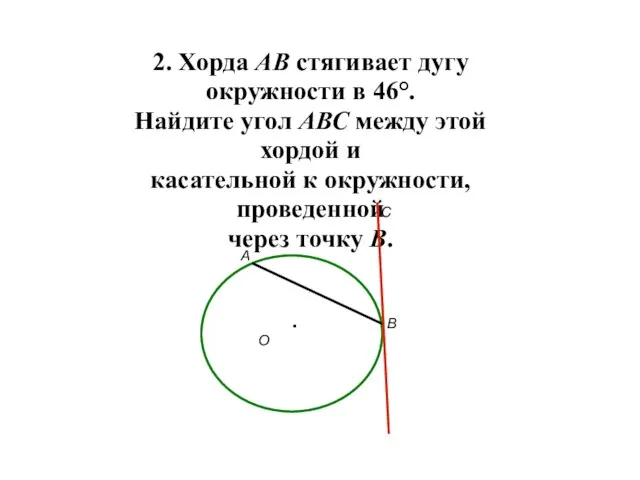
- 5. 2. Хорда АВ стягивает дугу окружности в 46°. Найдите угол АВС между этой хордой и касательной
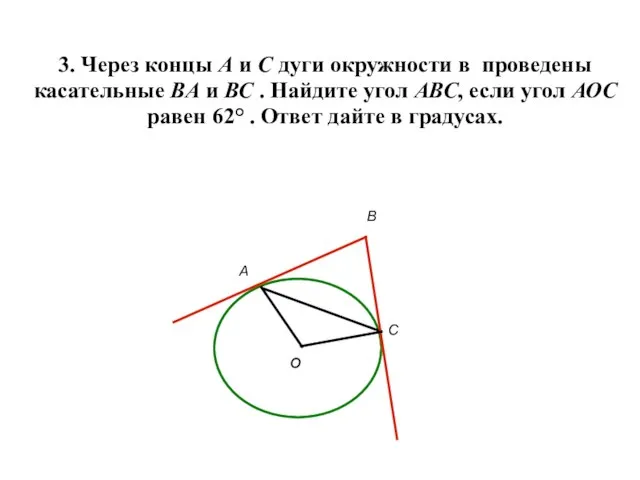
- 6. 3. Через концы А и С дуги окружности в проведены касательные ВА и ВС . Найдите
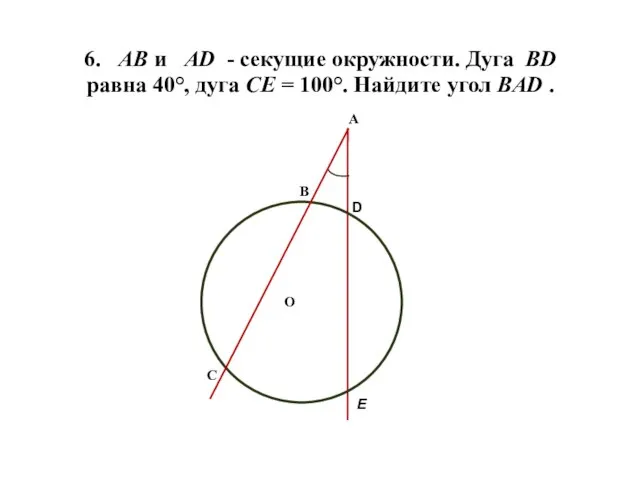
- 7. 6. АВ и AD - секущие окружности. Дуга ВD равна 40°, дуга СЕ = 100°. Найдите
- 8. Тема : «Пропорциональность отрезков хорд, касательных и секущих»
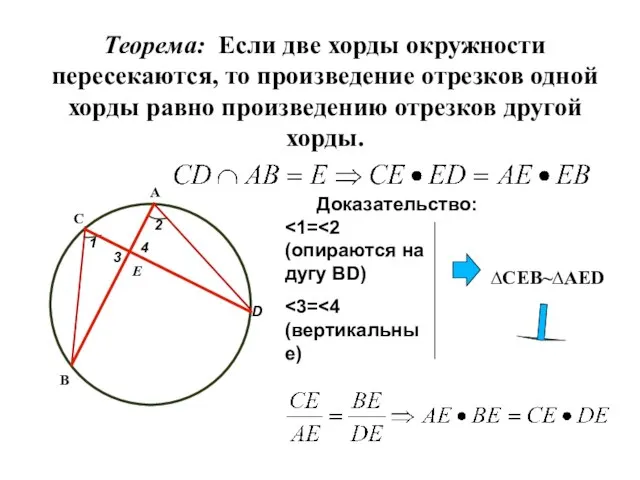
- 9. Теорема: Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
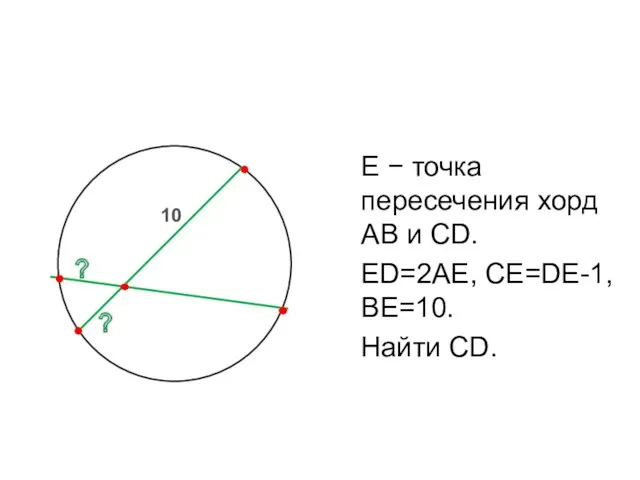
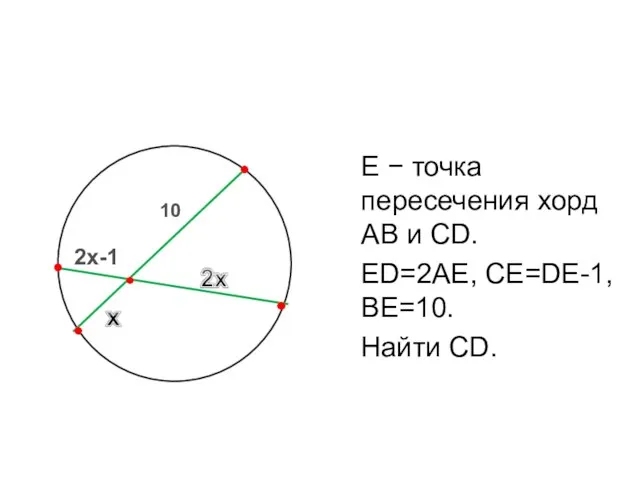
- 10. А В С D Е 10 ? E − точка пересечения хорд AB и CD. ED=2AE,
- 11. А В С D Е 10 E − точка пересечения хорд AB и CD. ED=2AE, CE=DE-1,
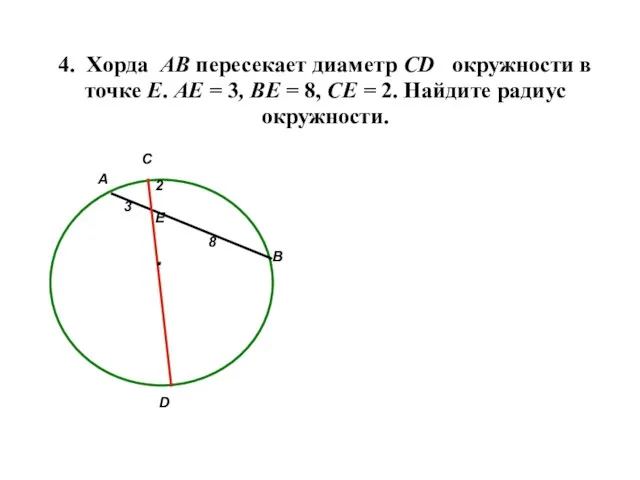
- 12. 4. Хорда АВ пересекает диаметр СD окружности в точке Е. АЕ = 3, ВЕ = 8,
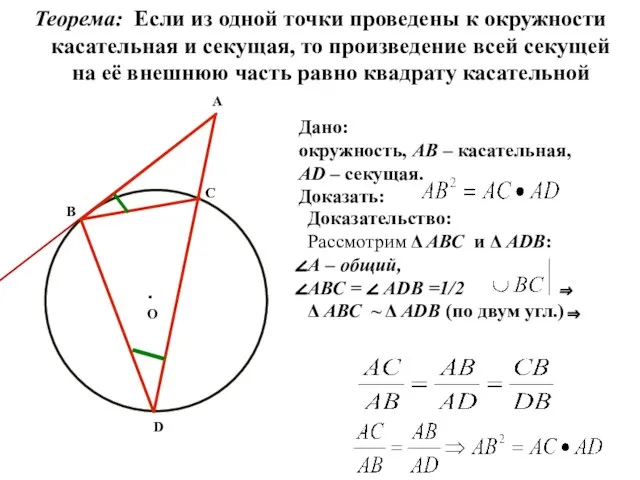
- 13. Теорема: Если из одной точки проведены к окружности касательная и секущая, то произведение всей секущей на
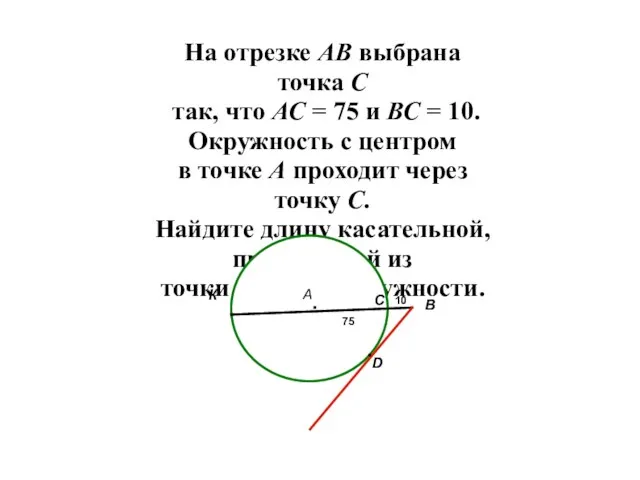
- 14. На отрезке АВ выбрана точка С так, что АС = 75 и ВС = 10. Окружность
- 15. Теорема: Если из точки, лежащей вне окружности, проведены две секущие, то произведение одной секущей на её
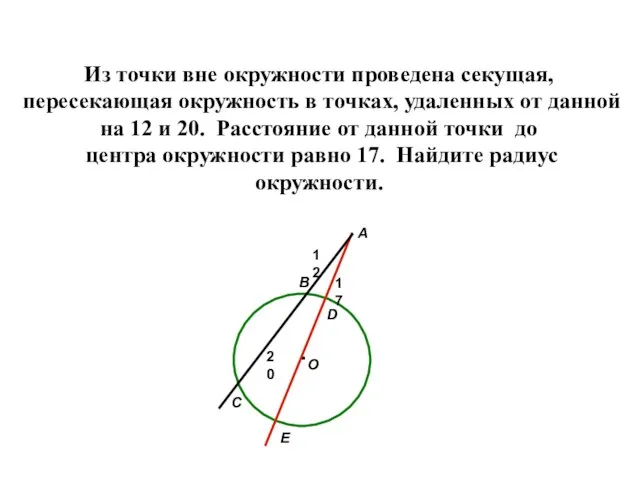
- 16. Из точки вне окружности проведена секущая, пересекающая окружность в точках, удаленных от данной на 12 и
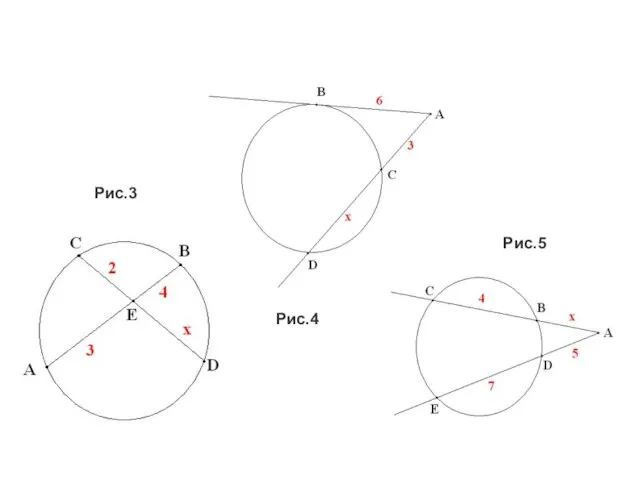
- 17. Рис.3 Рис.4 Рис.5
- 19. Скачать презентацию


 Учимся писать цифры с Дракошей
Учимся писать цифры с Дракошей Методы отбора единиц наблюдения для выборочной совокупности. Возможные типы систематических ошибок оценки в исследованиях
Методы отбора единиц наблюдения для выборочной совокупности. Возможные типы систематических ошибок оценки в исследованиях Применение векторного и смешанного произведений в решении задач С2
Применение векторного и смешанного произведений в решении задач С2 Математика. 2 класс. Задачи
Математика. 2 класс. Задачи О подобии произвольных фигур
О подобии произвольных фигур Презентация на тему Сложение и вычитание трехзначных чисел (2 класс)
Презентация на тему Сложение и вычитание трехзначных чисел (2 класс)  Определители второго и третьего порядка
Определители второго и третьего порядка Аттестационная работа. Элективный кружок, как элемент проектной деятельности
Аттестационная работа. Элективный кружок, как элемент проектной деятельности Урок математики. Замени произведение суммой
Урок математики. Замени произведение суммой Порядок выполнения действий в числовых выражениях
Порядок выполнения действий в числовых выражениях Основы теории измерений
Основы теории измерений Формулы сокращенного умножения
Формулы сокращенного умножения Задачи на готовых чертежах (геометрия, 7 класс)
Задачи на готовых чертежах (геометрия, 7 класс) Решение функции
Решение функции Сложение и вычитание. Разминка
Сложение и вычитание. Разминка Математический КВН
Математический КВН Итогово-обобщающий урок. Площадь. Теорема Пифагора
Итогово-обобщающий урок. Площадь. Теорема Пифагора Квадратные уравнения. 8 класс
Квадратные уравнения. 8 класс Презентация на тему Виды алгоритмов
Презентация на тему Виды алгоритмов  Тренажёр. Сложение в пределах 20
Тренажёр. Сложение в пределах 20 Математика (1 класс)
Математика (1 класс) Многогранники
Многогранники Викторина по геометрии
Викторина по геометрии Variācijas, permutācijas, kombinācijas
Variācijas, permutācijas, kombinācijas Презентация по математике "Правило умножения для комбинаторных задач" -
Презентация по математике "Правило умножения для комбинаторных задач" -  Почти все об углах
Почти все об углах Чему научились во 2 классе
Чему научились во 2 классе Блок случайных событий
Блок случайных событий