Теорема об отрезках пересекающихся хорд

ПРОВЕРЯЕМ ДОМАШНЕЕ ЗАДАНИЕ

ЗАДАЧИ НА ГОТОВЫХ ЧЕРТЕЖАХ
самостоятельная работа
выполнить в тетрадке (чертить не надо, записать только номер задания и ответ)

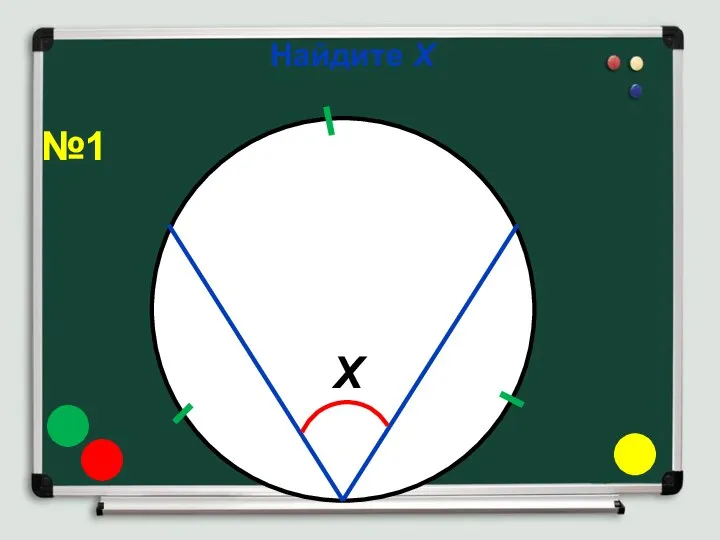
Найдите Х
Х
№1

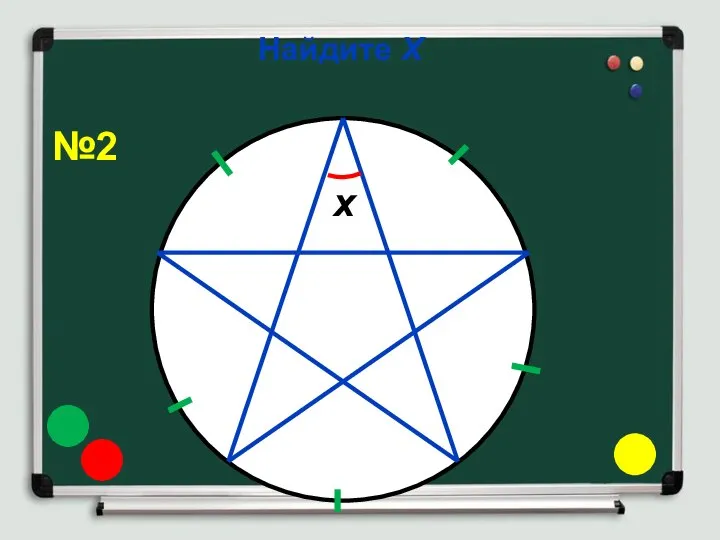
Найдите Х
x
№2

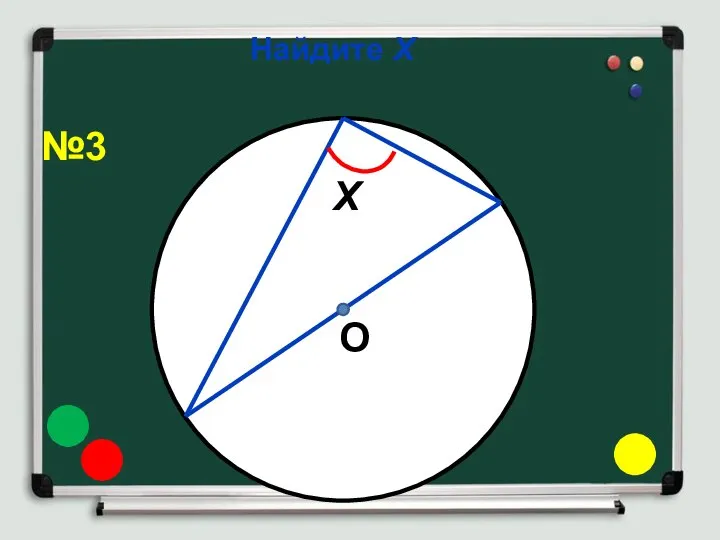
Найдите Х
О
Х
№3

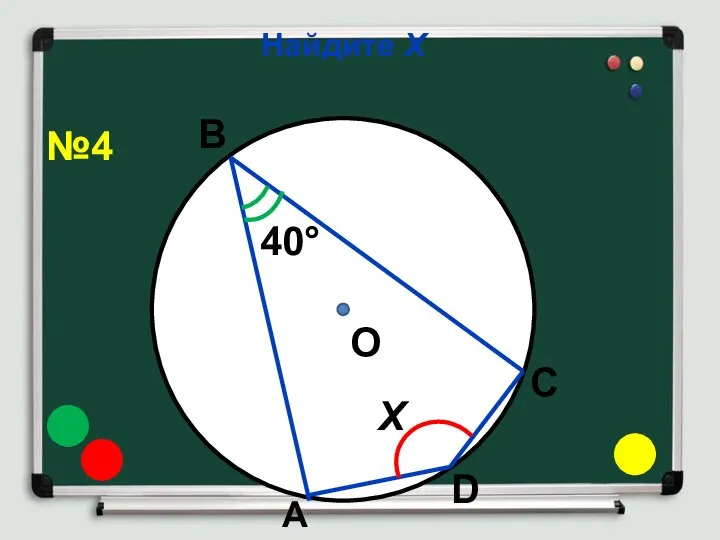
Найдите Х
О
40°
Х
В
А
С
D
№4

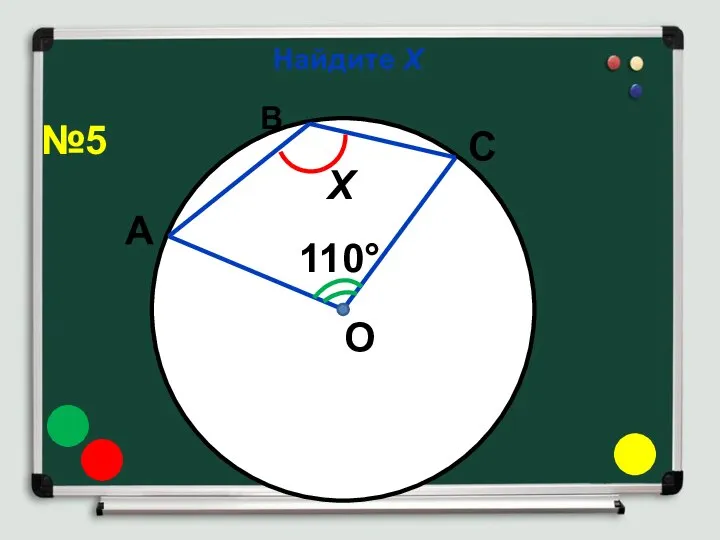
Найдите Х
О
110°
Х
А
С
В
№5

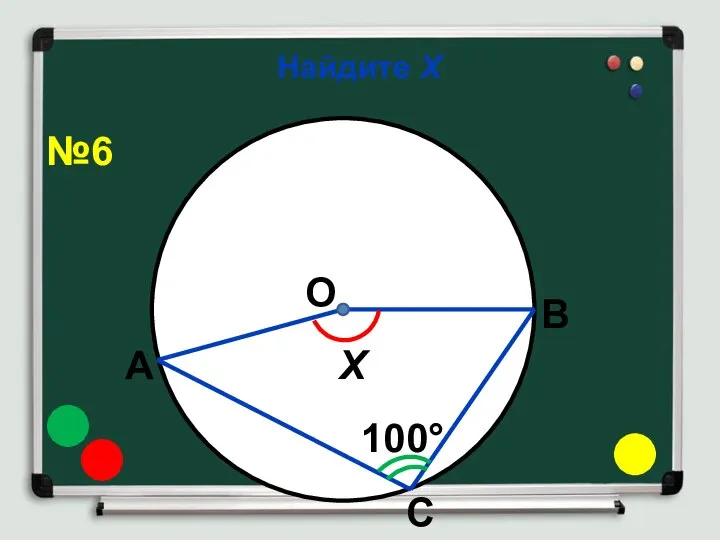
Найдите Х
О
100°
Х
А
В
С
№6

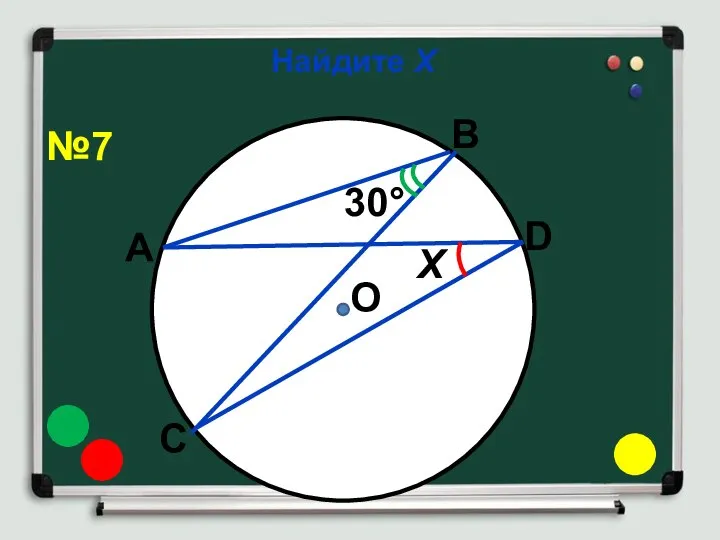
Найдите Х
О
30°
Х
№7
А
В
С
D

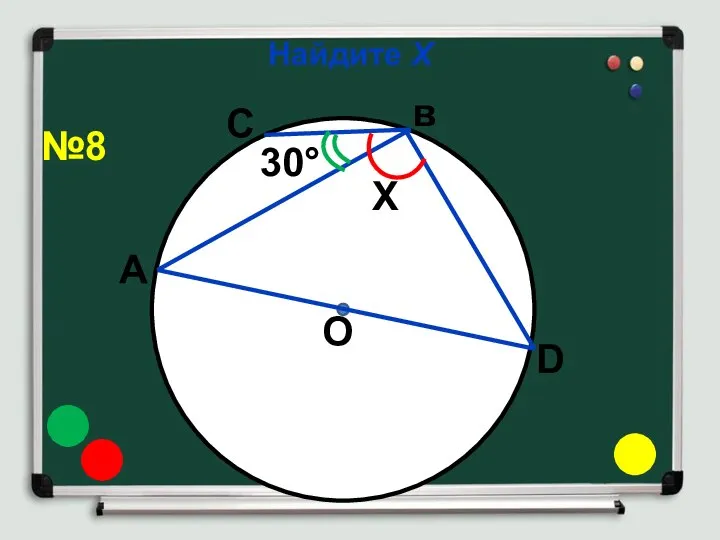
Найдите Х
О
30°
Х
А
С
в
D
№8

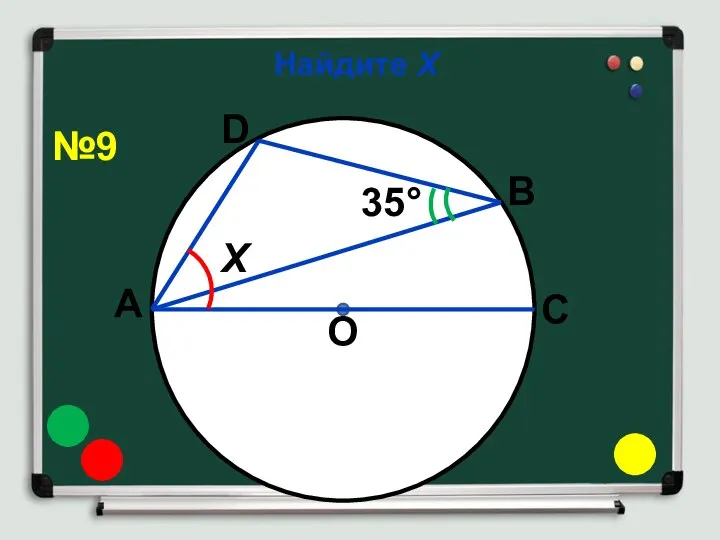
Найдите Х
О
35°
Х
А
С
В
D
№9

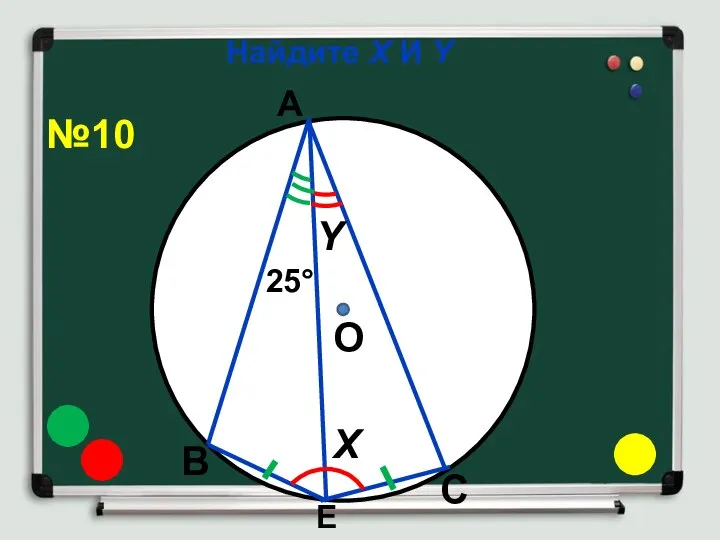
Найдите Х И Y
О
Х
Y
25°
А
В
С
Е
№10

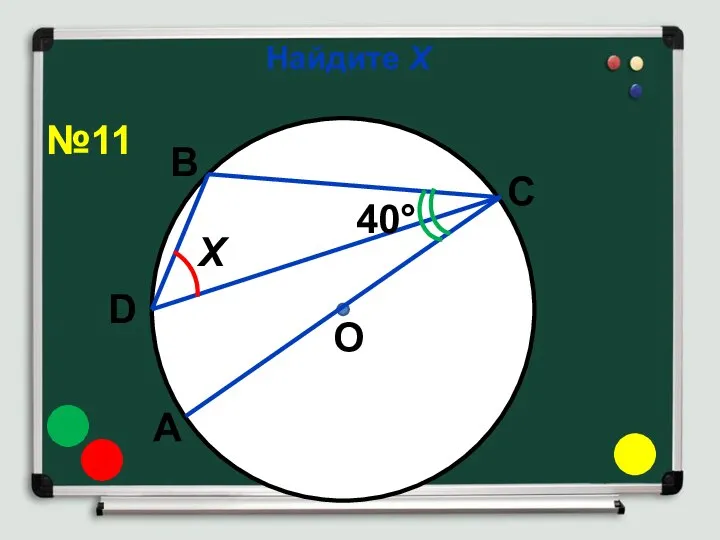
Найдите Х
Х
О
40°
А
D
В
С
№11

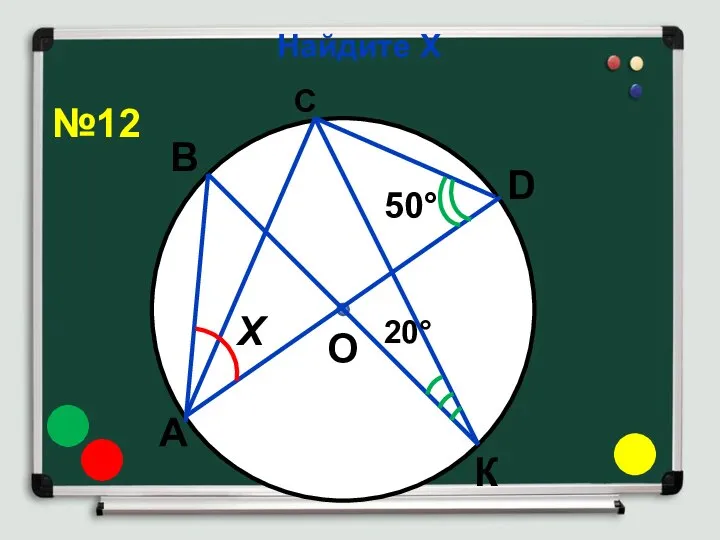
Найдите Х
В
К
А
D
О
С
Х
50°
20°
№12

Задача: Найти АЕ , если ВЕ=4 см, DE = 6 см ,СЕ=2см.
Доказать , треугольник АЕС подобен треуголь нику DBE.
А
Е
D
C
В
Решение.
АЕС подобен DEB т.к.
угол AED и угол ABD вписанные и
опираются на одну дугу. Угол AEC
И угол DEB равны как вертикальные
( первый признак подобия), отсюда
Стороны треугольников пропорциональны
AE : ED = BE: CE, AE : 6= 4: 2
отсюда АЕ = 6 * 4 :2 =12см.

Задача : Докажите , что если две хорды AB и CD окружности пересекаются в точке Е , то АЕ * ВЕ =СЕ *DE.
А
D
C
B
1
2
E
Доказательство :
Рассмотрим треугольники ADE и СВЕ. на Углы 1 и 2 равны, т. к они вписанные и опираются на одну и ту же дугу BD . Углы 3 и 4 равны как вертикальные. Следовательно треугольники подобны по первому признаку.
Отсюда AE : CE =DE: BE или
AE *BE=CE*DE.

План-конспект доказательства теоремы.
а
1) треугольники АСЕ и DBE подобны т. к угол А равен углу D как вписанные углы , опирающиеся на дугу ВС , углы AEC и DEB равны как вертикальные.
2) AE:DE= CE:BE
3) AE*BE= CE*DE.
. СТР 170 ТЕОРЕМА

Домашнее задание:
Стр.167 П.71 , стр.184 вопрос14, № 666(б), № 671(б)