Презентация на тему Многогранники. Призма

Многогранники
- Теория
- Правильные многогранники
- Призма

Многогранники
Многогранником называется поверхность, составленная из многоугольников, ограничивающих некоторое геометрическое тело.

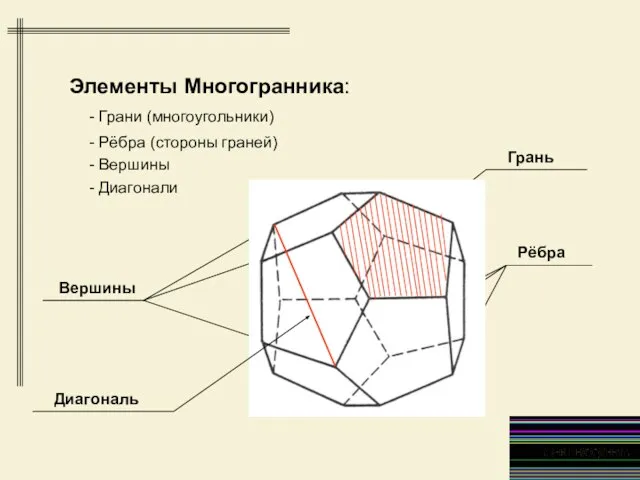
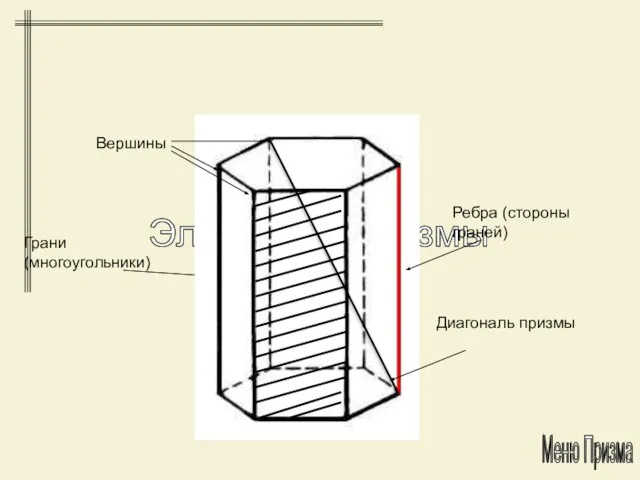
Элементы Многогранника:
- Грани (многоугольники)
- Рёбра (стороны граней)
- Вершины
- Диагонали

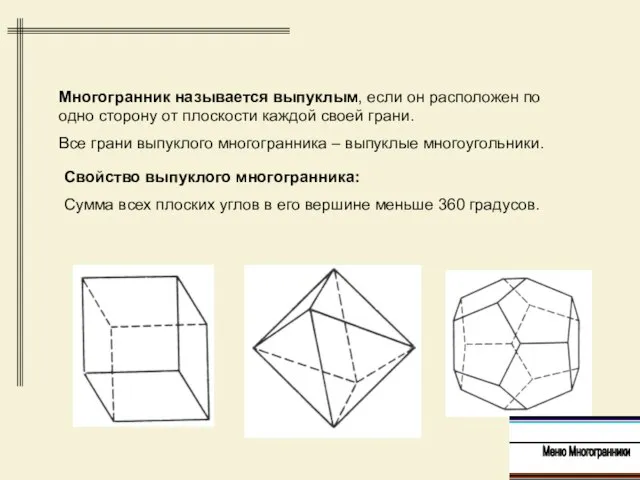
Свойство выпуклого многогранника:
Сумма всех плоских углов в его вершине меньше 360 градусов.
Многогранник называется выпуклым, если он расположен по одно сторону от плоскости каждой своей грани.
Все грани выпуклого многогранника – выпуклые многоугольники.

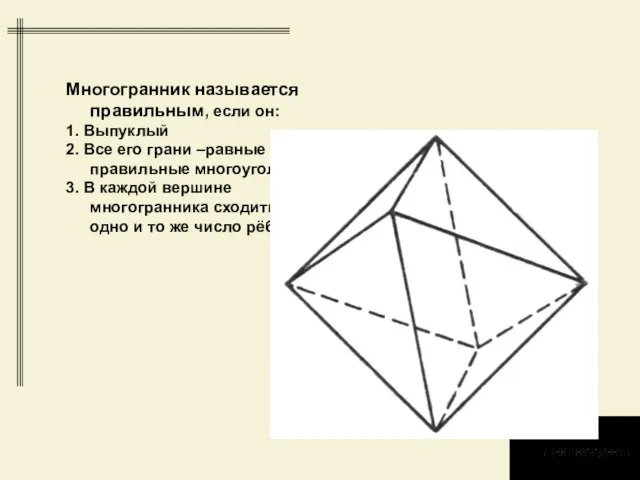
Многогранник называется правильным, если он:
1. Выпуклый
2. Все его грани –равные правильные многоугольники
3. В каждой вершине многогранника сходиться одно и то же число рёбер

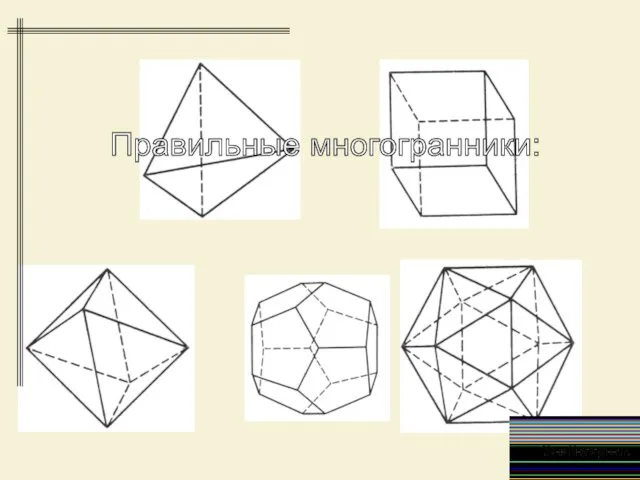
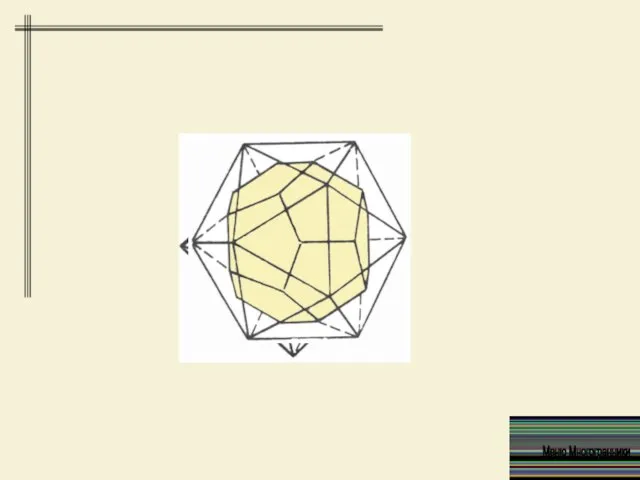
Правильные многогранники:

Призма
- Теория
- Элементы
- Нахождение площадей
- Задачи

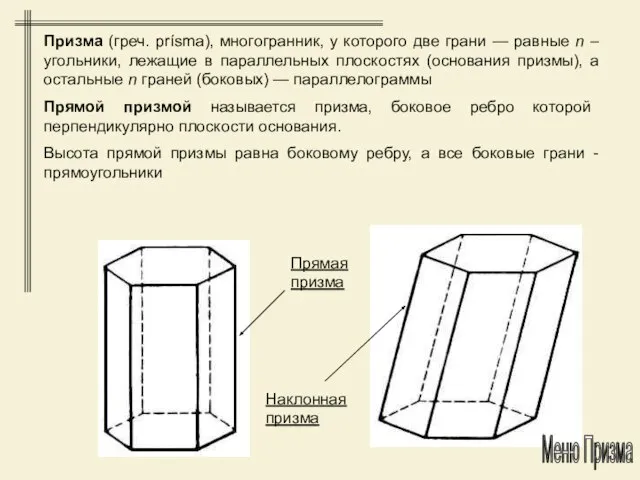
Призма (греч. prísma), многогранник, у которого две грани — равные n –угольники, лежащие в параллельных плоскостях (основания призмы), а остальные n граней (боковых) — параллелограммы
Прямой призмой называется призма, боковое ребро которой перпендикулярно плоскости основания.
Высота прямой призмы равна боковому ребру, а все боковые грани - прямоугольники
Прямая призма
Меню Призма
Наклонная призма

Элементы призмы
Меню Призма

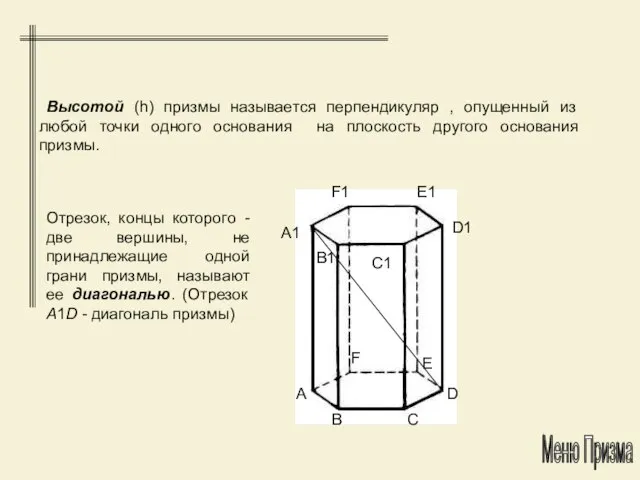
Высотой (h) призмы называется перпендикуляр , опущенный из любой точки одного основания на плоскость другого основания призмы.
Отрезок, концы которого - две вершины, не принадлежащие одной грани призмы, называют ее диагональю. (Отрезок A1D - диагональ призмы)
Меню Призма

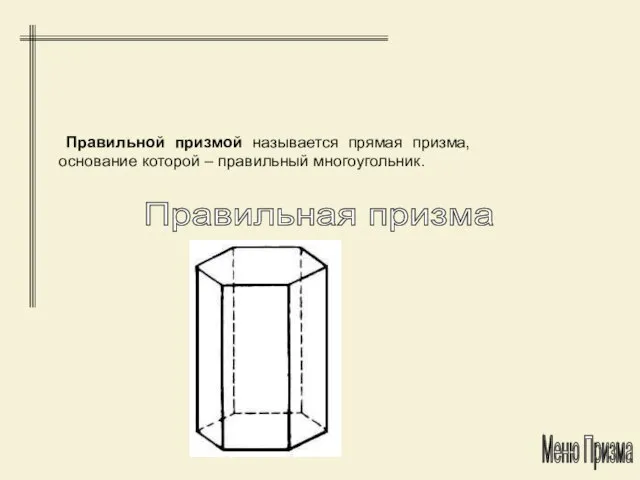
Правильная призма
Правильной призмой называется прямая призма, основание которой – правильный многоугольник.
Меню Призма

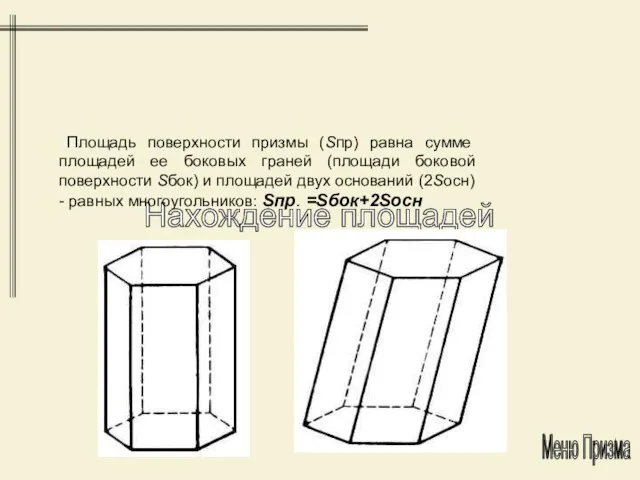
Нахождение площадей
Площадь поверхности призмы (Sпр) равна сумме площадей ее боковых граней (площади боковой поверхности Sбок) и площадей двух оснований (2Sосн) - равных многоугольников: Sпр. =Sбок+2Sосн
Меню Призма

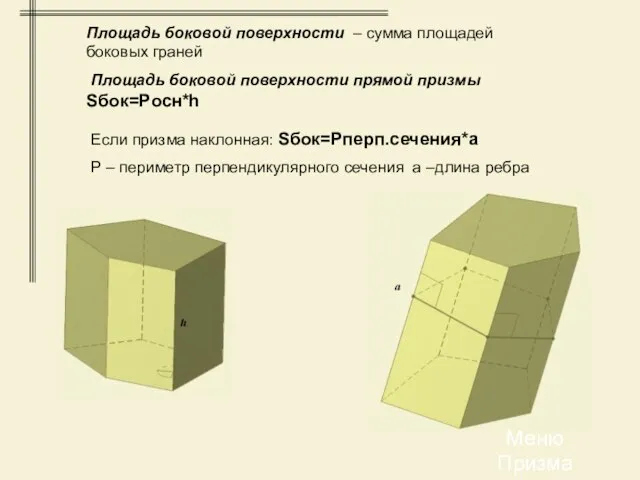
Площадь боковой поверхности – сумма площадей боковых граней
Площадь боковой поверхности прямой призмы Sбок=Pосн*h
Если призма наклонная: Sбок=Pперп.сечения*a
P – периметр перпендикулярного сечения a –длина ребра
Меню
Призма

Объём призмы
Меню
Призма

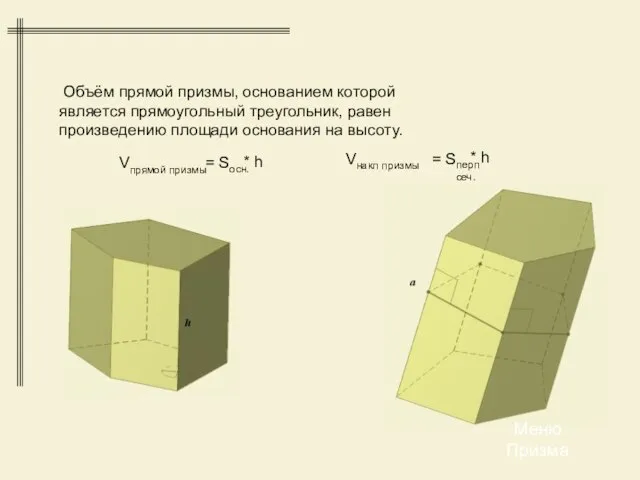
Объём прямой призмы, основанием которой является прямоугольный треугольник, равен произведению площади основания на высоту.
Меню
Призма

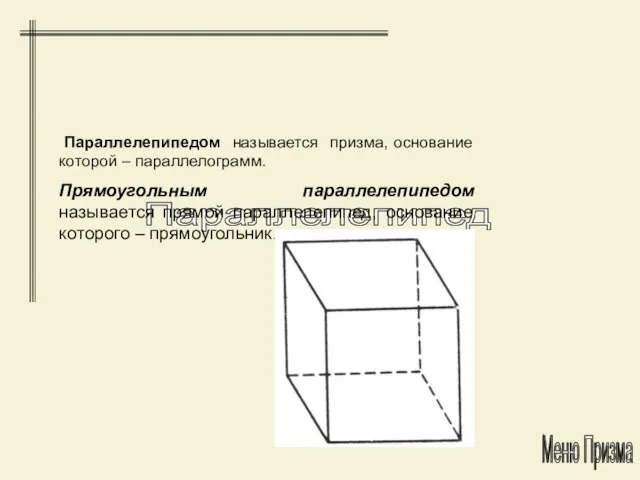
Параллелепипед
Параллелепипедом называется призма, основание которой – параллелограмм.
Прямоугольным параллелепипедом называется прямой параллелепипед, основание которого – прямоугольник.
Меню Призма

Свойства параллелепипеда
Меню Призма
Противоположные грани параллелепипеда равны параллельны
Все четыре диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
Сумма квадратов диагоналей параллелепипеда равна сумме квадратов всех его ребер.
Боковые грани прямого параллелепипеда – прямоугольники.
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.

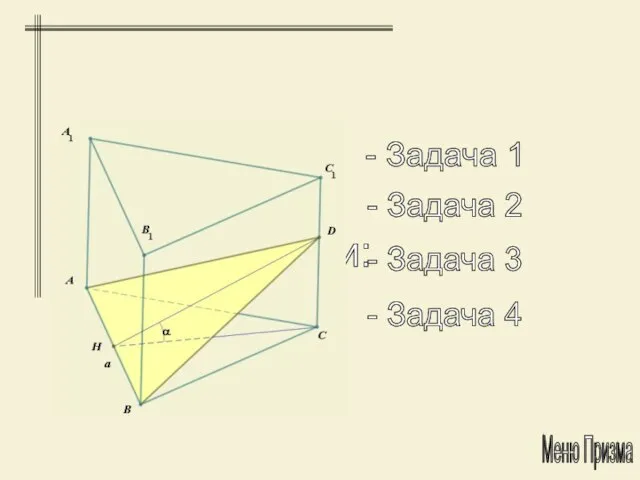
Задачи:
- Задача 1
- Задача 2
- Задача 3
- Задача 4
Меню Призма

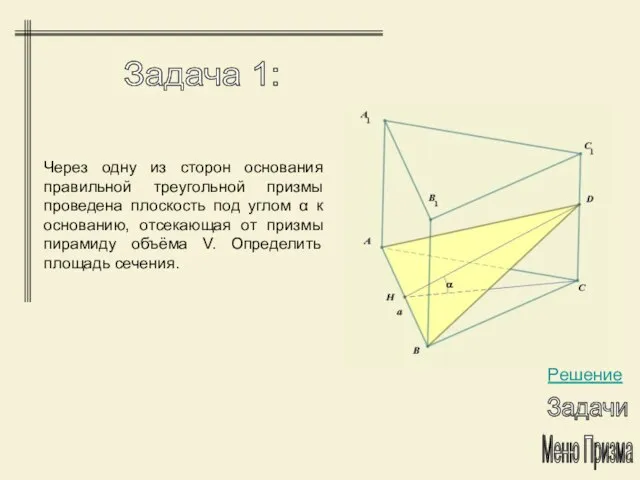
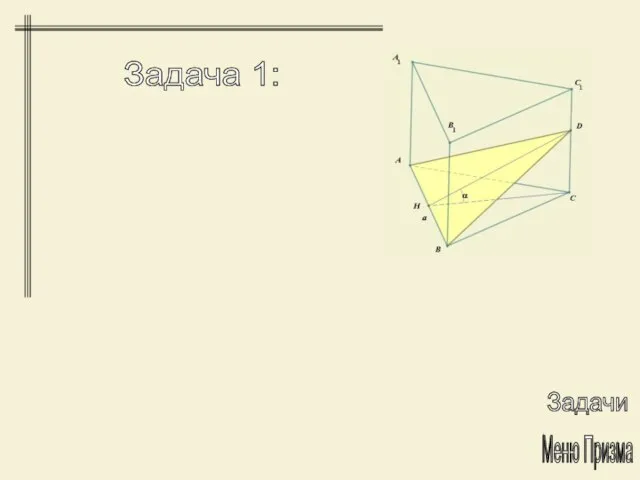
Через одну из сторон основания правильной треугольной призмы проведена плоскость под углом α к основанию, отсекающая от призмы пирамиду объёма V. Определить площадь сечения.
Задача 1:
Меню Призма
Задачи
Решение

Задача 1:
Меню Призма
Задачи

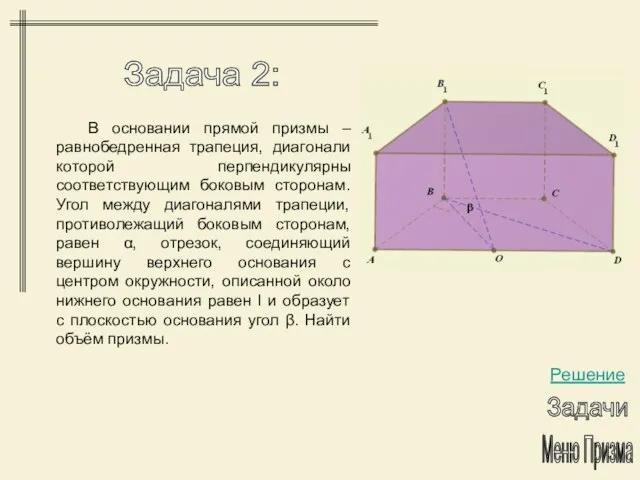
Задача 2:
Меню Призма
Решение
Задачи
В основании прямой призмы – равнобедренная трапеция, диагонали которой перпендикулярны соответствующим боковым сторонам. Угол между диагоналями трапеции, противолежащий боковым сторонам, равен α, отрезок, соединяющий вершину верхнего основания с центром окружности, описанной около нижнего основания равен l и образует с плоскостью основания угол β. Найти объём призмы.

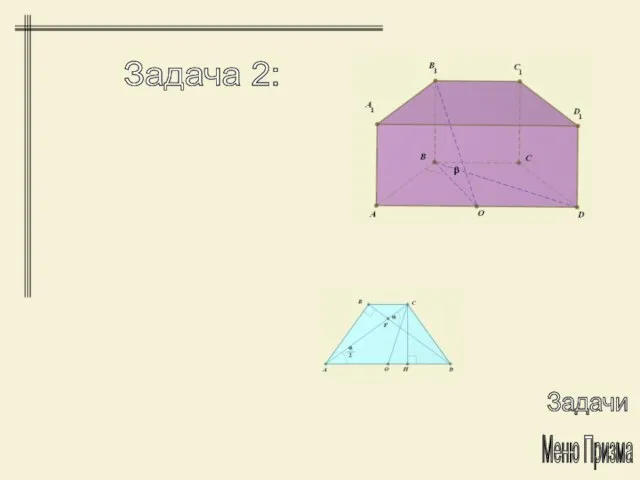
Задачи
Меню Призма
Задача 2:

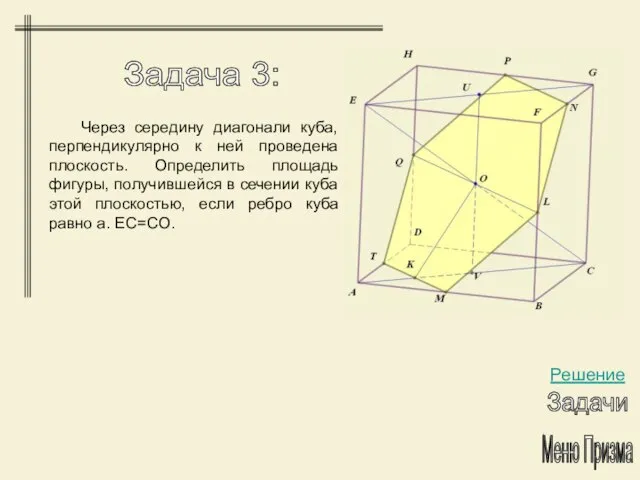
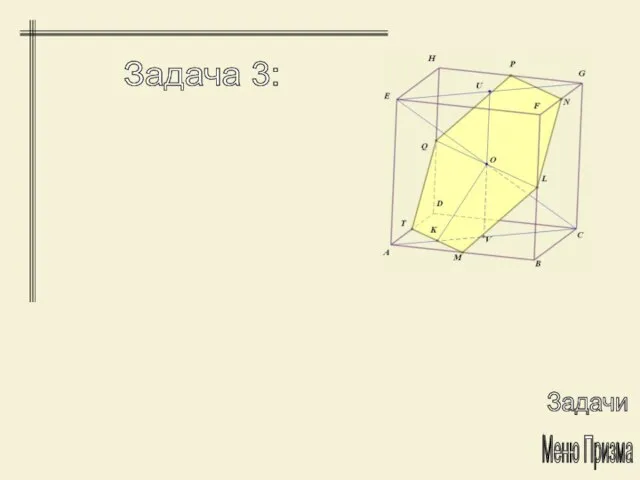
Меню Призма
Задача 3:
Решение
Задачи
Через середину диагонали куба, перпендикулярно к ней проведена плоскость. Определить площадь фигуры, получившейся в сечении куба этой плоскостью, если ребро куба равно a. EC=CO.

Задачи
Меню Призма
Задача 3:

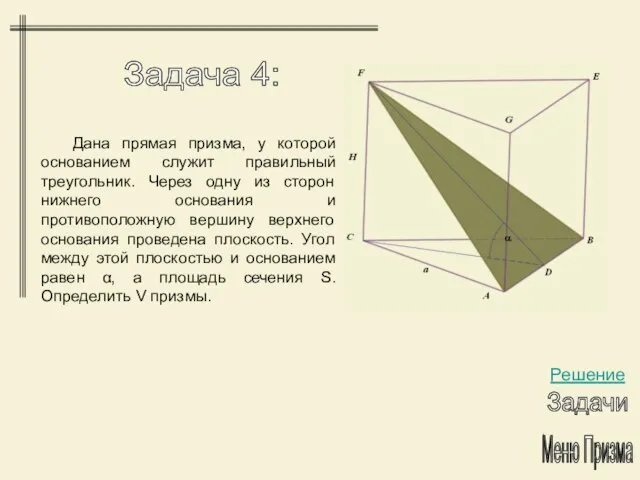
Меню Призма
Задача 4:
Решение
Задачи
Дана прямая призма, у которой основанием служит правильный треугольник. Через одну из сторон нижнего основания и противоположную вершину верхнего основания проведена плоскость. Угол между этой плоскостью и основанием равен α, а площадь сечения S. Определить V призмы.