Системы принятия решений. Определения

Пусть ϕ(y) является вещественной функцией, определенной в области Q мерного евклидова пространства RN и принимающая конечные значения в каждой точке множества Q.
Определения
Определение 1.1. Если существует точка y* ∈ Q такая, что
тогда φ(y) достигает своей точной нижней грани в области Q, а y* называется точкой глобального (абсолютного) минимума или глобальным минимайзером..
Значение φ* = φ(y*) называется наименьшим значением или значением глобального оптимума (минимума) функции φ в Q и обозначается как
Обозначим через

Определения
Обозначим множество всех точек y*∈ Q , удовлетворяющих (1.2) как
.
Определение 1.4. Будем называть задачей оптимизации задачу следующего вида: найти заданные экстремальные характеристики функции φ(y) в области Q.
Определение 1.3. Если функция φ(y) в области Q имеет единственный локальный минимум, она называется унимодальной, если несколько – многоэкстремальной.

Постановка задач оптимизации
Постановка А. Найти точную нижнюю грань функции φ(y)
Постановка B. Найти точную нижнюю грань (1.5) и, если множество точек глобального минимума (1.4) не пусто, найти хотя бы одну точку y* = Q*.
Постановка C. Найти точную нижнюю грань из (1.5) и все точки глобального минимума (1.4) (или удостовериться, что множество Q* пусто).
Постановка D. Найти координаты и значения всех локальных минимумов функции φ(y) в области Q.
Постановка E. Найти локальный минимум функции φ(y) в области Q.

Постановка задач оптимизации
Общую форму задачи оптимизации будем записывать в виде
Функция ϕ(y) в (1.6) называется целевой функцией, минимизируемой функцией, или оптимизируемой функцией, область Q называется допустимой областью, а элементы области Q - допустимыми точками.
Если заведомо известно, что целевая функция достигает своей точной нижней грани в допустимой области, задачу оптимизации будем записывать в виде
Что касается поиска максимума, то достаточно заметить, что
поэтому поиск максимума элементарно сводится к поиску минимума функции -ϕ(y).

Численные методы оптимизации

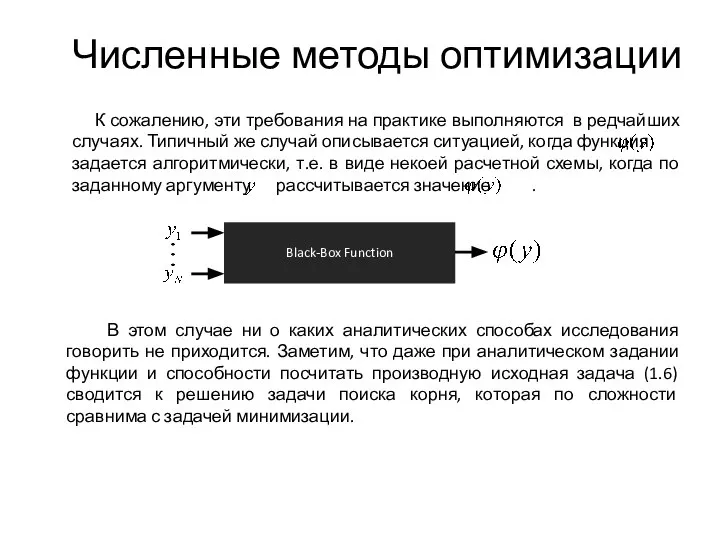
Численные методы оптимизации
В этом случае ни о каких аналитических способах исследования говорить не приходится. Заметим, что даже при аналитическом задании функции и способности посчитать производную исходная задача (1.6) сводится к решению задачи поиска корня, которая по сложности сравнима с задачей минимизации.

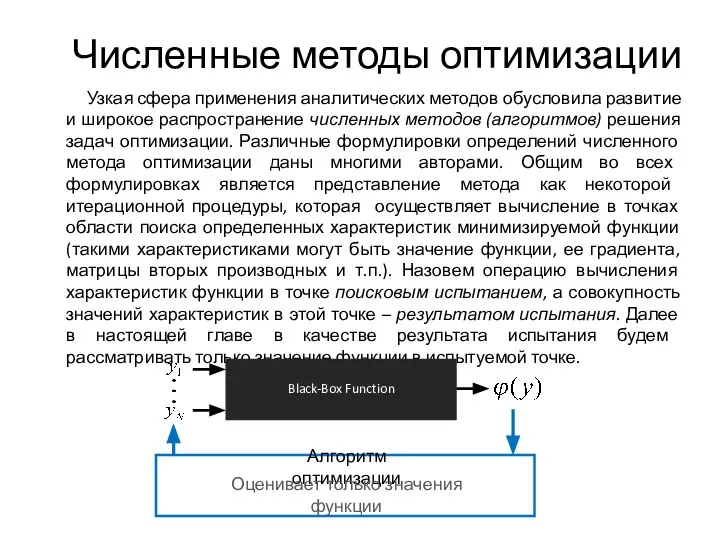
Численные методы оптимизации
Узкая сфера применения аналитических методов обусловила развитие и широкое распространение численных методов (алгоритмов) решения задач оптимизации. Различные формулировки определений численного метода оптимизации даны многими авторами. Общим во всех формулировках является представление метода как некоторой итерационной процедуры, которая осуществляет вычисление в точках области поиска определенных характеристик минимизируемой функции (такими характеристиками могут быть значение функции, ее градиента, матрицы вторых производных и т.п.). Назовем операцию вычисления характеристик функции в точке поисковым испытанием, а совокупность значений характеристик в этой точке – результатом испытания. Далее в настоящей главе в качестве результата испытания будем рассматривать только значение функции в испытуемой точке.

Модель алгоритма

Модель алгоритма
{Gk}, k=1,2,… - функционалы выбора точек испытаний;
{Ek}, k=1,2,… - функционалы построения оценок решения;
{Hk}, k=1,2,… - функционалы правила остановки.
Следующим важным этапом построения модели вычислений является выбор алгоритма (метода) решения задачи. В самом общем виде численный метод решения задачи из класса представляет собой набор (кортеж)
(1.8)

Вычислительная схема алгоритма
Выбирается точка первого испытания с номером k=1:
Пусть выбрана точка k-го испытания .
Вычисляем значение Поисковая (апостериорная) информация о функции
Апостериорный класс
(1.9)
(1.10)
(1.11)

Вычислительная схема алгоритма
Определяется текущая оценка экстремума (приближенное решение)
Вычисляется точка очередного испытания
Определяется величина
(1.12)

Пример: перебор по равномерной сетке
или

Свойства методов оптимизации
Идеально: за конечное число испытаний найти точное решение задачи.

Сходимость метода оптимизации
Определение 1.5. Последовательность испытаний сходится к решению задачи оптимизации, определенному соответствующей постановкой, если:
1. существует подпоследовательность такая, что
2. если искомое решение включает одну или несколько координат экстремумов, для каждой такой координаты найдется подпоследовательность последовательности испытаний ,
сходящаяся к этой точке.