Содержание
- 2. Статистический критерий - это решающее правило, обеспечивающее принятие истинной и отклонение ложной гипотезы с высокой вероятностью
- 3. Типы статистических критериев По используемым параметрам: Параметрические - основаны на конкретном типе распределения генеральной совокупности (как
- 4. По цели: Меры сравнения – позволяют проверить гипотезу о наличии или отсутствии различий между переменными. Пример:
- 5. По цели (продолжение) Многомерные критерии – выполняют такие интеллектуальные функции как структурирование эмпирической информации (факторный анализ),
- 6. По типу выборки: Критерии для несвязанных выборок Несвязанные (независимые) выборки - выборки, в которые объекты исследования
- 7. По типу выборки (продолжение): Критерии для связанных выборок Связанные (зависимые) выборки - каждое наблюдение одной выборки
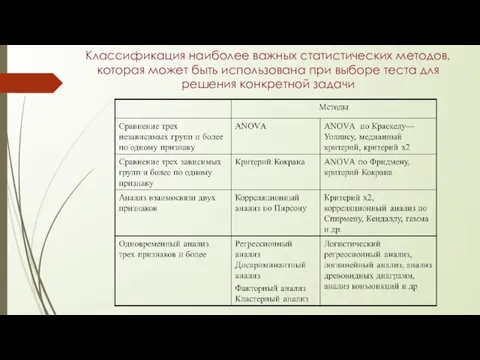
- 8. Классификация наиболее важных статистических методов, которая может быть использована при выборе теста для решения конкретной задачи
- 9. Классификация наиболее важных статистических методов, которая может быть использована при выборе теста для решения конкретной задачи
- 10. Меры сравнения Q - Критерий Розенбаума U критерий Манна-Уитни Н - критерий Крускала-Уоллиса S – критерий
- 11. Правила ранжирования: №1. Наименьшему значению начисляется ранг 1. №2. Наибольшему значению начисляется ранг, соответствующий количеству ранжируемых
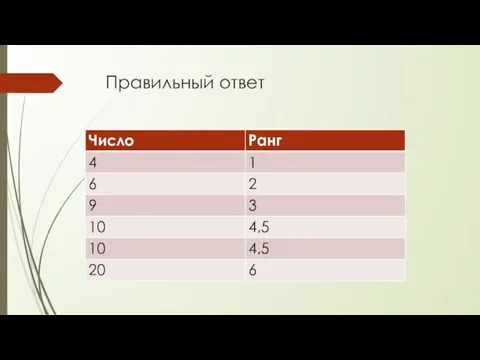
- 12. Проранжируйте следующие числа 4 20 6 10 9 10
- 13. Правильный ответ
- 14. Непараметрические меры различий
- 15. Q - Критерий Розенбаума Назначение критерия: Используется для оценки различии между двумя выборками по уровню какого-либо
- 16. Q - Критерий Розенбаума (ограничения) 1. В каждой из сопоставляемых выборок должно быть не менее 11
- 17. U критерий Манна-Уитни Назначение: предназначен для оценки различий между двумя выборками по уровню какого-либо признака, количественно
- 18. U критерий Манна-Уитни (ограничения) 1. В каждой выборке должно быть не менее 3 наблюдений; допускается, чтобы
- 19. Н - критерий Крускала-Уоллиса Назначение критерия: предназначен для оценки различии одновременно между тремя, четырьмя и т.д.
- 20. Н - критерий Крускала-Уоллиса (ограничения) 1. При сопоставлении 3-х выборок допускается, чтобы в одной из них
- 21. Н - критерий Крускала-Уоллиса (графическое отображение) Критерий Н оценивает общую сумму перекрещивающихся зон при сопоставлении всех
- 22. S – критерий тенденций Джонкира Назначение критерия: Критерий S предназначен для выявления тенденций изменения признака при
- 23. S – критерий тенденций Джонкира (графическое отображение)
- 24. S – критерий тенденций Джонкира (ограничения) Измерение может быть проведено в шкале порядка, интервалов или отношений.
- 25. Параметрические меры различий
- 26. F критерий Фишера Назначение критерия: Применяется для проверки равенства дисперсий двух выборок. Гипотезы: Н0: Величина дисперсии
- 27. F критерий Фишера (примеры использования) 1. При использовании критерия Стьюдента имеет смысл предварительно проверить гипотезу о
- 28. F критерий Фишера (ограничения) 1. Измерение может быть проведено в шкале интервалов и отношений. 2. Сравниваемые
- 29. T-критерий Стьюдента для двух независимых выборок Назначение: сравнения средних значений двух независимых между собой выборок. Гипотеза:
- 30. T-критерий Стьюдента для двух независимых выборок (ограничения) Сравниваемые значения не составляют пару коррелирующих значений Распределение признаков
- 31. T-критерий Стьюдента для двух зависимых выборок Назначение: сравнения средних значений двух зависимых между собой выборок. Гипотезы:
- 32. T-критерий Стьюдента для двух зависимых выборок (ограничения) Сравниваемые значения составляют пару коррелирующих значений Распределение признаков в
- 33. T-критерий Стьюдента для одной выборки Назначение: наблюдаемое среднее (выборка) сравнивается с ожидаемым (или эталонным) средним выборки
- 35. Скачать презентацию






























 Признаки равенства треугольников
Признаки равенства треугольников Дифференциальные уравнения высших порядков
Дифференциальные уравнения высших порядков Параллельность прямых и плоскостей (10 класс)
Параллельность прямых и плоскостей (10 класс) Умножение обыкновенных дробей
Умножение обыкновенных дробей TA&Ml_ukr_1
TA&Ml_ukr_1 Инженерно-вычислительные технологии
Инженерно-вычислительные технологии Применение производной к исследованию функции
Применение производной к исследованию функции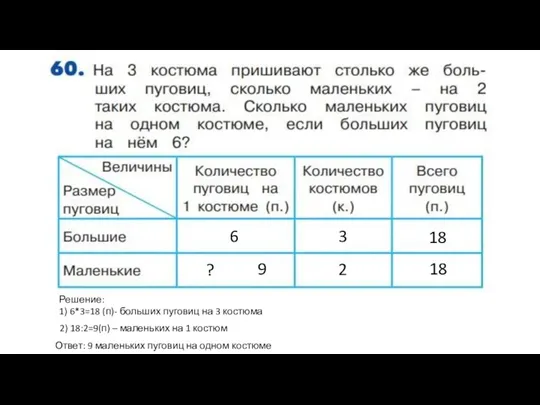 Задача о костюмах
Задача о костюмах Нахождение неизвестного вычитаемого
Нахождение неизвестного вычитаемого Дискретные случайные величины
Дискретные случайные величины Задание В11, открытого банка ЕГЭ по математике (часть 1)
Задание В11, открытого банка ЕГЭ по математике (часть 1) Критерий линейной корреляции Пирсона
Критерий линейной корреляции Пирсона Построение сечений
Построение сечений Логарифмические уравнения и методы их решения
Логарифмические уравнения и методы их решения Решение уравнений сводящихся к линейным
Решение уравнений сводящихся к линейным Золотое сечение в архитектуре, скульптуре, живописи
Золотое сечение в архитектуре, скульптуре, живописи Задачи на построение
Задачи на построение Сравнение предметов по некоторой величине без её измерения: выше - ниже, шире - уже
Сравнение предметов по некоторой величине без её измерения: выше - ниже, шире - уже Презентация на тему Сложение и вычитание чисел 5,6,7,8,9 (1 класс)
Презентация на тему Сложение и вычитание чисел 5,6,7,8,9 (1 класс)  Равносильные уравнения и неравенства
Равносильные уравнения и неравенства Компланарные векторы
Компланарные векторы Цветочное настроение (порядковый счет)
Цветочное настроение (порядковый счет) Венегрет. Урок
Венегрет. Урок Презентация по математике "Портреты учёных математиков" -
Презентация по математике "Портреты учёных математиков" -  График функций. Домашняя работа по алгебре
График функций. Домашняя работа по алгебре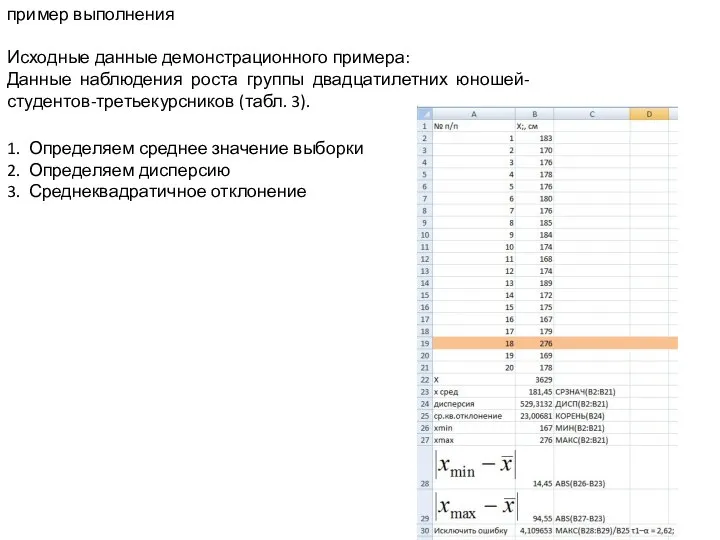 Данные наблюдения роста группы двадцатилетних юношей студентов
Данные наблюдения роста группы двадцатилетних юношей студентов Ломаная линия
Ломаная линия Решение тригонометрических уравнений. 10 класс
Решение тригонометрических уравнений. 10 класс