Содержание
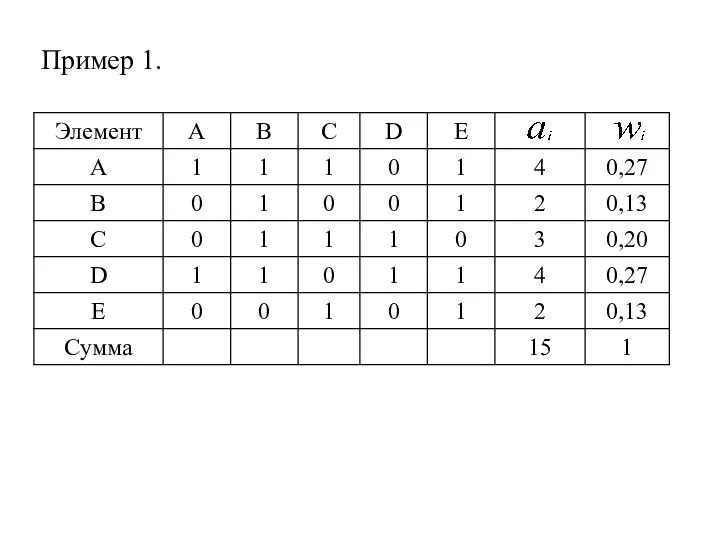
- 2. Определение нормированных приоритетов по матрице парных сравнений без учета интенсивности предпочтений Нормированный приоритет i-го объекта определяется
- 3. Пример 1.
- 4. Определение собственного вектора матрицы парных сравнений с учетом интенсивности предпочтений Для определения собственного вектора матрицы, соответствую-щего
- 5. Таким образом, элементы матрицы Х соответствуют системе уравнений: Перенося члены из правой части в левую, получим:
- 6. Пример 2: Дана следующая матрица парных сравнений с учетом интенсивности предпочтений. Требуется найти нормированные приоритеты объектов.
- 8. Принимаем Х1=1, получаем: Складывая 2 и 3 уравнения, находим Х2 = 0,356 Из 1 уравнения выражаем
- 9. Нормируем собственный вектор Х из единицы и получаем нормированные приоритеты: Проверка правильности расчетов:
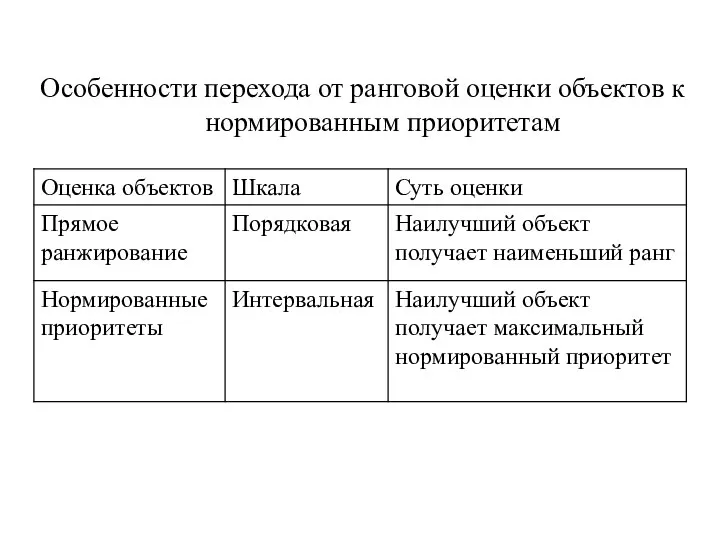
- 10. Особенности перехода от ранговой оценки объектов к нормированным приоритетам
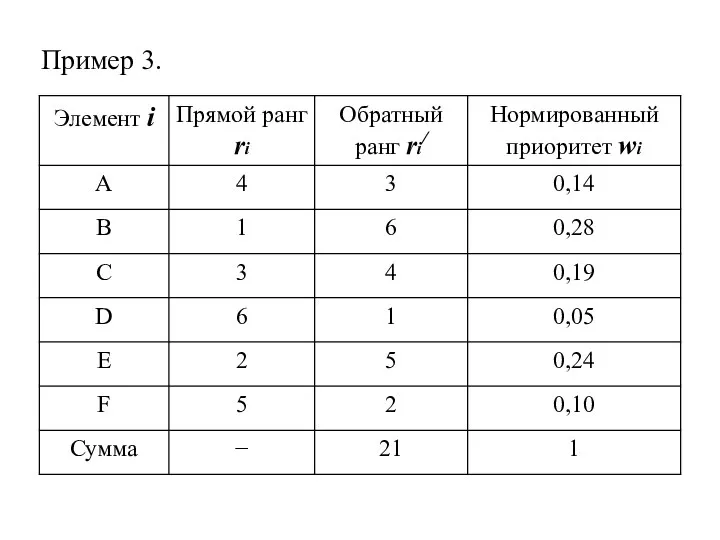
- 11. Для унификации направленности предпочтений объектам присваиваются обратные ранги, вычисляемые по формуле: где n – количество объектов;
- 12. Пример 3.
- 14. Скачать презентацию




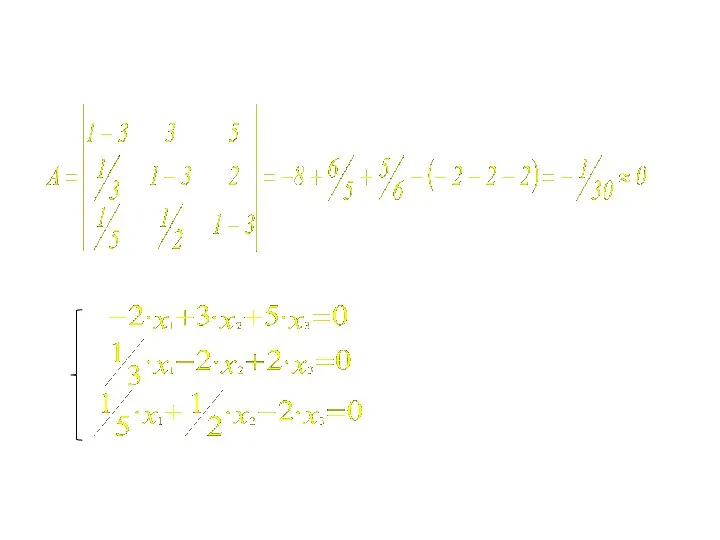



 Нулевой угловой коэффицент
Нулевой угловой коэффицент В стране математики
В стране математики Тригонометрия. Контрольная работа
Тригонометрия. Контрольная работа Площади. Формула Пика
Площади. Формула Пика Функции многих переменных: частные производные, дифференциалы. Лекция 2
Функции многих переменных: частные производные, дифференциалы. Лекция 2 Первые уроки в 5 кассе
Первые уроки в 5 кассе Решение задач с помощью рациональных уравнений. 8 класс
Решение задач с помощью рациональных уравнений. 8 класс Таблица сложения
Таблица сложения Подготовка к ЕГЭ (профильный уровень). Теория вероятности
Подготовка к ЕГЭ (профильный уровень). Теория вероятности Элементы теории вероятности
Элементы теории вероятности График функции. Урок применения знаний и умений. Класс: 8
График функции. Урок применения знаний и умений. Класс: 8 Иррациональные уравнения
Иррациональные уравнения Смежные углы
Смежные углы Определение арифметического корня п-ой степени
Определение арифметического корня п-ой степени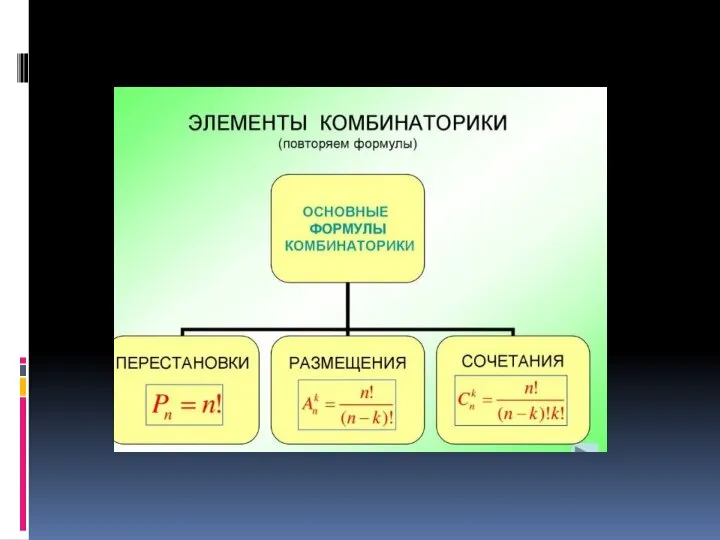 Основные понятия комбинаторики
Основные понятия комбинаторики Презентация на тему Буквенные выражения (2 класс)
Презентация на тему Буквенные выражения (2 класс) 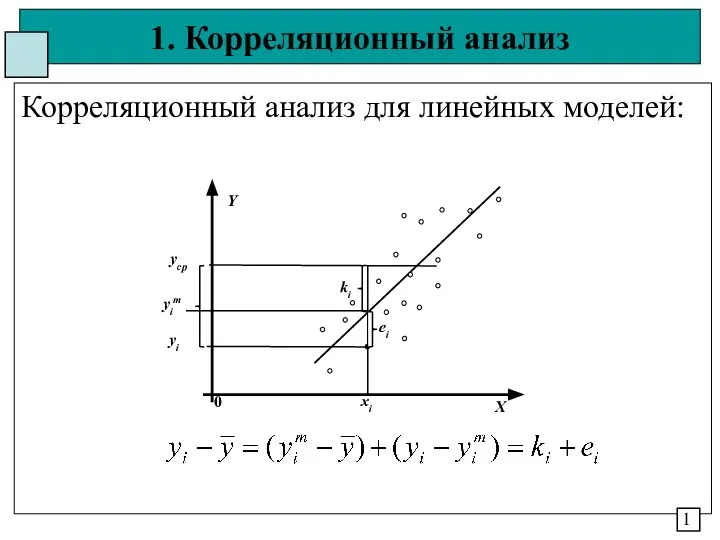 Корреляционный анализ для линейных моделей
Корреляционный анализ для линейных моделей Введение таблицы умножения (Школа XXI века. Рудницкая В.Н )
Введение таблицы умножения (Школа XXI века. Рудницкая В.Н ) Решение тригонометрических уравнений
Решение тригонометрических уравнений Площадь криволинейной трапеции и интеграл
Площадь криволинейной трапеции и интеграл Спиннеры и метематика
Спиннеры и метематика krivye-vtorogo-poryadka (1)
krivye-vtorogo-poryadka (1) Обратные матрицы
Обратные матрицы Сравнение моделей
Сравнение моделей Признак перпендикулярности прямой и плоскости
Признак перпендикулярности прямой и плоскости Презентация на тему Многоугольники (1 класс)
Презентация на тему Многоугольники (1 класс)  Сантиметр Цель. В ходе практической работы и наблюдений познакомить учащихся 1 класса с единицей измерения длины – сантиметром.
Сантиметр Цель. В ходе практической работы и наблюдений познакомить учащихся 1 класса с единицей измерения длины – сантиметром. Перпендикулярность прямых в пространстве
Перпендикулярность прямых в пространстве