Слайд 2Лекция №3
План
1. Понятие равносильности формул логики высказываний.
2. Основные равносильности формул логики высказываний.

Слайд 3Понятие равносильности формул
Рассмотрим две формулы логики высказываний: , .
Составим для них таблицы
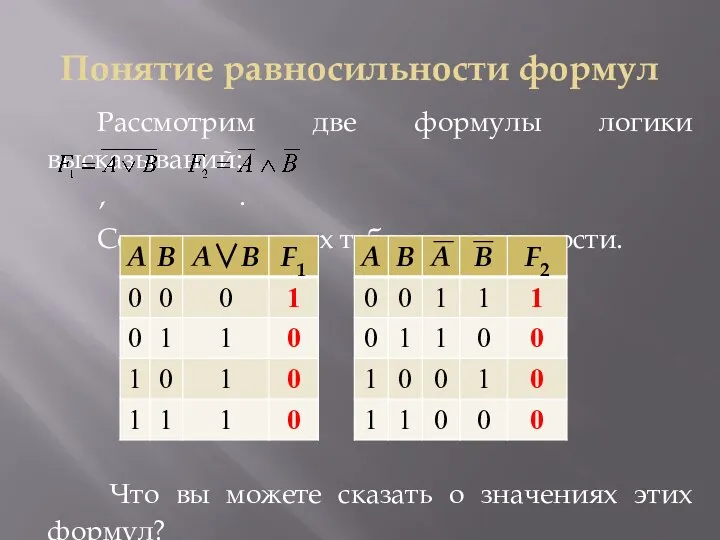
истинности.
Что вы можете сказать о значениях этих формул?
Слайд 4Понятие равносильности формул
Определение. Формулы F1 и F2 называются равносильными, если они принимают

одинаковые истинностные значения при любом наборе значений переменных, входящих в эти формулы. Обозначают: F1 ≡ F2.
Теорема. Формулы F1 и F2 являются равносильными, если формула F1 ↔ F2 является тождественно истинной (тавтологией).
Справедливость утверждения непосредственно следует из определения эквиваленции.
Слайд 5Основные равносильности формул (законы логики)
Одной из задач логики является установление равносильности логических

формул или их упрощение. Построение таблиц истинности в этом случае может оказаться очень громоздким или вообще не давать нужный результат. В таких случаях целесообразно осуществить равносильные преобразования формул.
Рассмотрим основные равносильности формул логики (законы логики) и правила преобразований формул логики.
Слайд 6Основные равносильности формул (законы логики)

Слайд 7Основные равносильности формул (законы логики)

Слайд 8Основные равносильности формул (законы логики)

Слайд 9Основные равносильности формул (законы логики)
При упрощении логических формул, как правило, исключают операции

импликации, эквиваленции, штрих Шеффера, стрелку Пирса и сложение по модулю 2, и осуществляют переход к стандартному базису логических функций, содержащему операции конъюнкции, дизъюнкции и отрицания. При этом добиваются, чтобы отрицания стояли только над отдельными переменными, а сами переменные или их отрицания связывались операциями дизъюнкции и конъюнкции.
Слайд 10Основные равносильности формул (законы логики)

Слайд 11Основные равносильности формул (законы логики)
При выполнении равносильных преобразований логических формул наряду с

перечисленными выше законами логики используют следующие правила преобразований:
Правило подстановки. Пусть F1 и F2 - равносильные формулы, содержащие некоторую формулу F. Если формулу F заменить в формулах F1 и F2 на формулу G, то формулы G1 и G2 также будут равносильными: G1≡G2.
.
Слайд 12Основные равносильности формул (законы логики)
Так, согласно правилу подстановки,
например, из равносильности формул
вытекает

равносильность формул
В данном случае в исходные формулы вместо формулы А мы подставили формулу А→С, при этом новые формулы также равносильны.
Слайд 13Основные равносильности формул (законы логики)
При выполнении равносильных преобразований логических формул наряду с

перечисленными выше законами логики используют следующие правила преобразований:
Правило замены. Пусть в формуле F1 выделена формула F и G - равносильная ей формула: F≡G. Если формулу F в формуле F1 заменить на формулу G, то полученная формула G1 будет равносильна формуле F1 : F1 ≡ G1.
.












 АВТОР: Краснова И.Я.
АВТОР: Краснова И.Я. Практическое применение теоремы косинусов и синусов. 9 класс
Практическое применение теоремы косинусов и синусов. 9 класс Сложение и вычитание в пределах 20. Повторение
Сложение и вычитание в пределах 20. Повторение Практический расчёт, оценка и прикидка. Подготовка к ЕГЭ
Практический расчёт, оценка и прикидка. Подготовка к ЕГЭ Функции и их свойства. Область определения и область значений функции
Функции и их свойства. Область определения и область значений функции Лекция№7
Лекция№7 Диаграммы
Диаграммы Преобразования графиков
Преобразования графиков Прятки с фигурами
Прятки с фигурами Решение систем неравенств (9 класс)
Решение систем неравенств (9 класс) Таблица сложения
Таблица сложения Подготовка к контрольной работе
Подготовка к контрольной работе ВПР. Решение задач
ВПР. Решение задач Закрепление. Повтори правила стр. 72, 74
Закрепление. Повтори правила стр. 72, 74 Площадь треугольника и биссектриса
Площадь треугольника и биссектриса Презентация на тему Призма. Построение сечений призмы плоскостями
Презентация на тему Призма. Построение сечений призмы плоскостями  Решение систем неравенств с одной переменной
Решение систем неравенств с одной переменной Математические ребусы
Математические ребусы Многоликая теорема Пифагора
Многоликая теорема Пифагора Задачи
Задачи Линейные дифференциальные уравнения первого порядка
Линейные дифференциальные уравнения первого порядка Postoroenie_gr_trigon_f
Postoroenie_gr_trigon_f ЕГЭ по профильной математике. Прототипы №1
ЕГЭ по профильной математике. Прототипы №1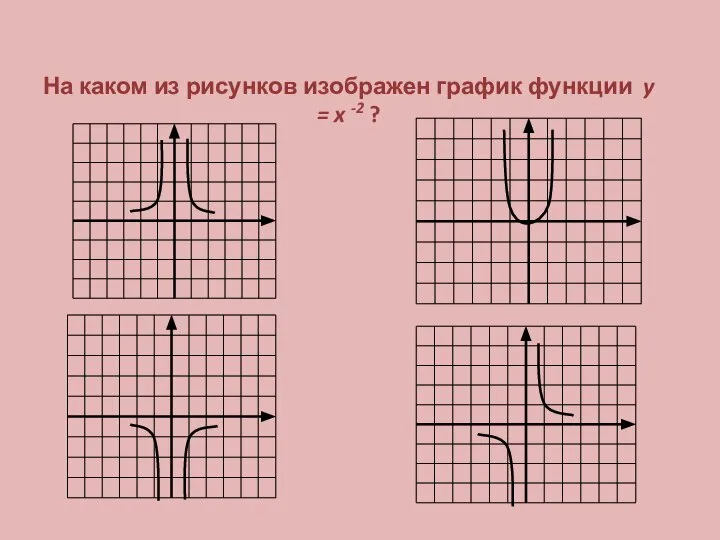 Степенная функция
Степенная функция Формула полной вероятности и Байеса
Формула полной вероятности и Байеса Равносильность уравнений. 11 класс
Равносильность уравнений. 11 класс Задачи, обратные данной
Задачи, обратные данной Единицы, десятки
Единицы, десятки