Содержание
- 2. Методы решения системы Прямые методы Метод Гаусса Метод Жордана-Гаусса Метод Крамера Матричный метод Метод прогонки Приближенные
- 3. Метод Гаусса
- 4. Гаусс Карл Фридрих (1777 - 1855) Выдающийся немецкий математик. Его труды глубоко повлияли на развитие математической
- 5. Теорема Кронекера - Капелли Система линейных уравнений тогда и только тогда совместна, когда ранг расширенной матрицы
- 6. Метод Гаусса Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к
- 7. Метод Гаусса: Пусть коэффициент а11 ≠ 0 (если он равен нулю, начать с какого-либо другого, отличного
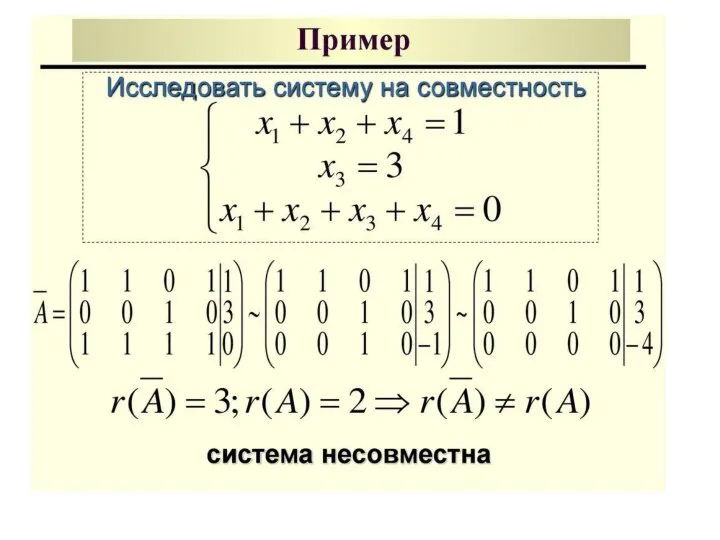
- 8. Исследование систем линейных уравнений: Если то система несовместна. Если (где n – число неизвестных), то система
- 9. П р а в и л о решения произвольной системы линейных уравнений. 1. Найти ранги основной
- 10. Неизвестные, коэффициенты при которых входят в базисный минор, называются главными; иx оставляют слева, а остальные n
- 14. Рассмотрим квадратную систему:
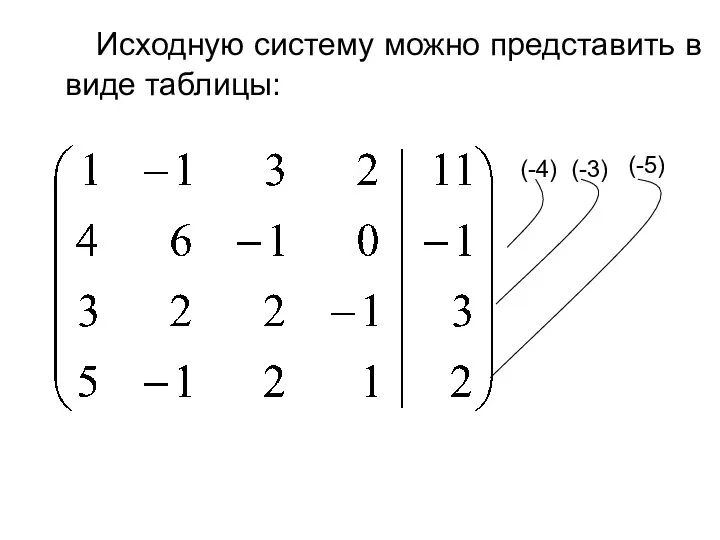
- 15. Исходную систему можно представить в виде таблицы: (-4) (-3) (-5)
- 16. (-1) 2 5 (-2)
- 19. Полученная матрица соответствует системе (из полученной системы найти неизвестные):
- 20. Решение систем линейных неоднородных уравнений Алгоритм построения общего решения неоднородной системы Вычислить и и установить совместность
- 21. 3. Рассмотрим уравнения системы (1), соответствующие базисному минору. Их будет r. 4. Неизвестные , коэффициенты которых
- 22. 5. Запишем уравнения системы (1), соответствующие базисному минору, в виде: слагаемые с базисными переменными оставим в
- 23. 6. Обозначим свободные переменные Выразим базисные переменные по формулам Крамера через параметры :
- 24. Решение систем линейных неоднородных уравнений В результате получим решение системы (1), которое называю общим решением системы.
- 25. Пример Найти общее и указать некоторое частное решение системы система совместна
- 26. Пример Базисный минор: Система из двух уравнений, соответствующих базисному минору: - базисные переменные - свободные переменные
- 27. Пример Базисные переменные модели выразим через свободные: Обозначим свободные переменные: Имеем:
- 28. Пример Выразим базисные переменные по формулам Крамера через параметры . Общее решение системы
- 30. Скачать презентацию












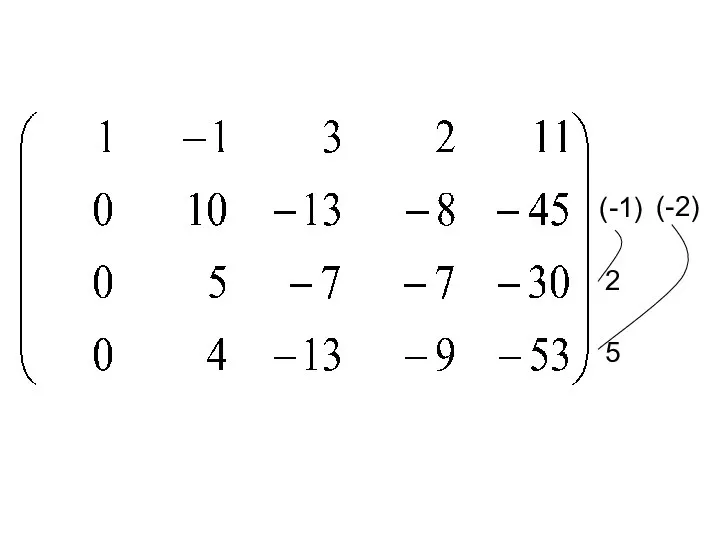












 Правильные многогранники
Правильные многогранники Действительный анализ2. Ступенчатые функции. Измеримые функции
Действительный анализ2. Ступенчатые функции. Измеримые функции Линейные уравнения. Решение задач с помощью линейных уравнений. 7 класс
Линейные уравнения. Решение задач с помощью линейных уравнений. 7 класс Вычисление производной
Вычисление производной Математика. Основные понятия математики
Математика. Основные понятия математики Презентация на тему Сложение чисел с разными знаками (6 класс)
Презентация на тему Сложение чисел с разными знаками (6 класс)  Разработка обучающей программы по нахождению элементов треугольника
Разработка обучающей программы по нахождению элементов треугольника Введение в алгебру
Введение в алгебру Конкурсное задание УРОК
Конкурсное задание УРОК Конкурс – олимпиада студентов ОЗТК по математике Математические старты 2018
Конкурс – олимпиада студентов ОЗТК по математике Математические старты 2018 Презентация на тему ГИА 2013. Модуль алгебра №6
Презентация на тему ГИА 2013. Модуль алгебра №6  Презентация на тему Сложение многозначных чисел
Презентация на тему Сложение многозначных чисел  Перпендикулярные прямые
Перпендикулярные прямые Площадь треугольника
Площадь треугольника Решение задач на применение аксиом стереометрии и их следствий
Решение задач на применение аксиом стереометрии и их следствий Презентация на тему Признаки делимости: практикум
Презентация на тему Признаки делимости: практикум  Решение тригонометрических уравнений
Решение тригонометрических уравнений Возведение в степень
Возведение в степень Космонавтика в примерах и задачах
Космонавтика в примерах и задачах Нумерология. Пифагор
Нумерология. Пифагор Длина. Выполни действия
Длина. Выполни действия Разложение правильной рациональной дроби на сумму простейших дробей. Лекция 2.2
Разложение правильной рациональной дроби на сумму простейших дробей. Лекция 2.2 Построение аксонометрических проекций геометрических фигур и тел
Построение аксонометрических проекций геометрических фигур и тел Теоретико-множественные преобразования
Теоретико-множественные преобразования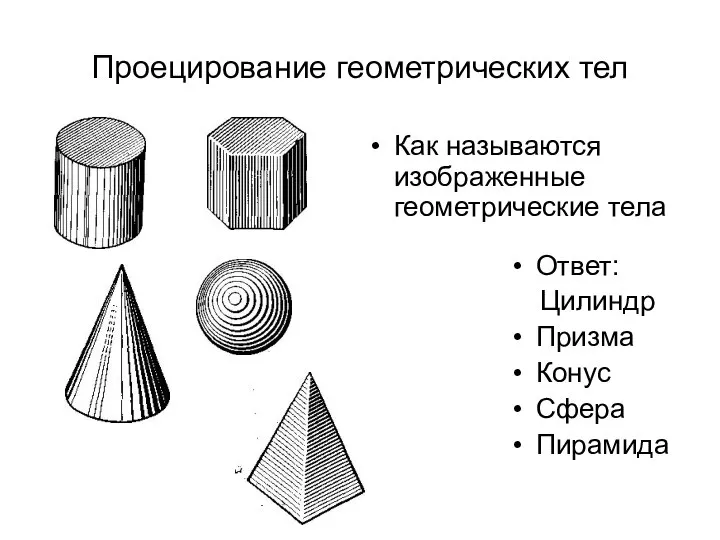 Построение геометрических тел
Построение геометрических тел Презентация на тему Призма
Презентация на тему Призма  Аксиомы стереометрии
Аксиомы стереометрии Упрощение логических операций
Упрощение логических операций