Содержание
- 2. Цель нашего урока целеполагание В комбинаторных задачах часто ставится вопрос о том, сколькими способами можно расположить
- 3. Что сделано дома: Вопросы и задания Подведение итогов, рефлексия, домашнее задание. а) В спартакиаде приняли участие
- 4. Математическая разминка Вхождение в тему урока и создание условий для осознанного восприятия нового материала. Сколько будет
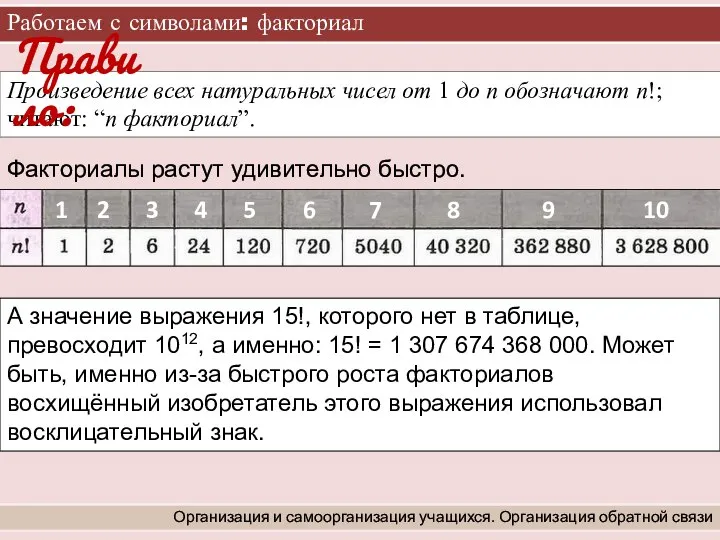
- 5. Произведение всех натуральных чисел от 1 до п обозначают п!; читают: “n факториал”. Работаем с символами:
- 6. Работаем с символами: факториал Организация и самоорганизация учащихся. Организация обратной связи да ? нет ? да
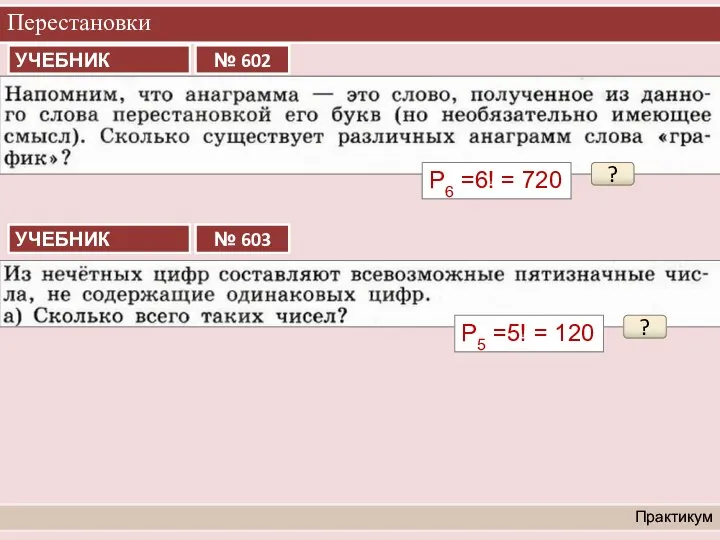
- 7. Перестановки Организация и самоорганизация учащихся. Организация обратной связи В турнире четверо участников. Сколькими способами могут распределиться
- 8. Перестановки Организация и самоорганизация учащихся. Организация обратной связи 8∙7∙6∙5∙4∙3∙2∙1 = 40320 ? 1 способ – умножение:
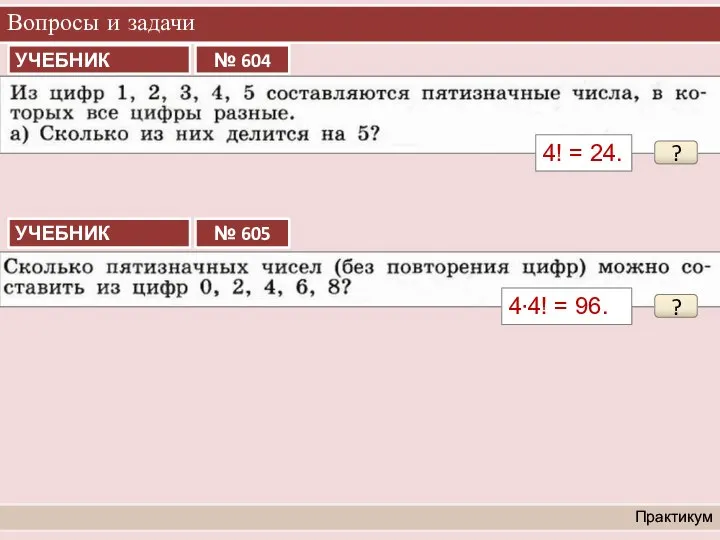
- 9. Перестановки Организация и самоорганизация учащихся. Организация обратной связи В расписании 7 класса на четверг должно быть
- 10. Перестановки Организация и самоорганизация учащихся. Организация обратной связи Сколькими способами можно составить расписание из тех же
- 11. Практическая ситуация Практикум ? Р3 =3! = 1∙2∙3 = 6 , нет.
- 12. Перестановки Практикум ? Р6 =6! = 720 ? Р5 =5! = 120
- 13. ? Перестановки Организация и самоорганизация учащихся. Организация обратной связи Сколькими способами из тех же шести предметов
- 14. Вопросы и задачи Практикум ? 4! = 24. ? 4∙4! = 96.
- 16. Скачать презентацию










 Сложение смешанных дробей
Сложение смешанных дробей Контрольная работа по математике. 8 класс
Контрольная работа по математике. 8 класс Уроки математики в Школе смешариков
Уроки математики в Школе смешариков Рекурсивные алгоритмы
Рекурсивные алгоритмы Треугольник. Первый признак равенства треугольников
Треугольник. Первый признак равенства треугольников Площадь и объём фигуры
Площадь и объём фигуры Всякая правильная математическая идея находит применение в том или ином деле
Всякая правильная математическая идея находит применение в том или ином деле Тождественные преобразования алгебраических выражений (часть 1)
Тождественные преобразования алгебраических выражений (часть 1) Интересные факты про математику
Интересные факты про математику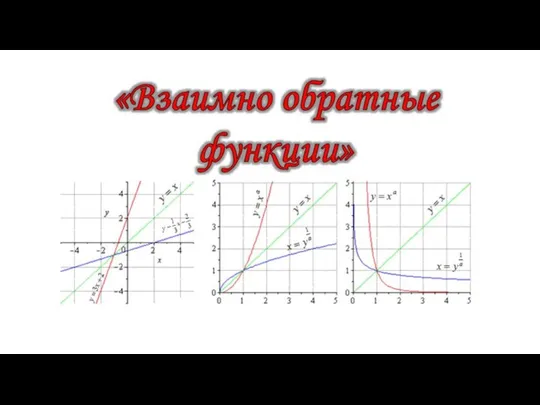 Взаимно обратные функции
Взаимно обратные функции Математика
Математика Геометрический и механический смысл производной
Геометрический и механический смысл производной Сложение и вычитание в пределах 20
Сложение и вычитание в пределах 20 Обратные тригонометрические функции и их свойства
Обратные тригонометрические функции и их свойства Приближенные значения чисел. Округление
Приближенные значения чисел. Округление Векторы. Действия с векторами
Векторы. Действия с векторами Математика и статистика для анализа данных
Математика и статистика для анализа данных Решение задач
Решение задач Десятичные и натуральные логарифмы
Десятичные и натуральные логарифмы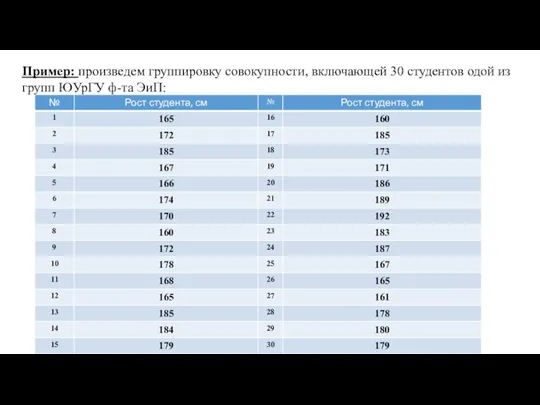 Группировка
Группировка Спасатели. Игра
Спасатели. Игра Задача № 5 з математики. Команда “Леонардо”
Задача № 5 з математики. Команда “Леонардо” Матрицы и действия над ними
Матрицы и действия над ними Интерполяционный многочлен Лагранжа
Интерполяционный многочлен Лагранжа Матрицы и определители
Матрицы и определители Соответствия между множествами. Отображения. Функции
Соответствия между множествами. Отображения. Функции Практикумы по задачам на готовых чертежах
Практикумы по задачам на готовых чертежах Нумерация. Сложение и вычитание. Геометрические фигуры и величины
Нумерация. Сложение и вычитание. Геометрические фигуры и величины