Содержание
- 2. Нелинейные уравнения f(x)=0 Алгебраические уравнения Трансцендентные уравнения
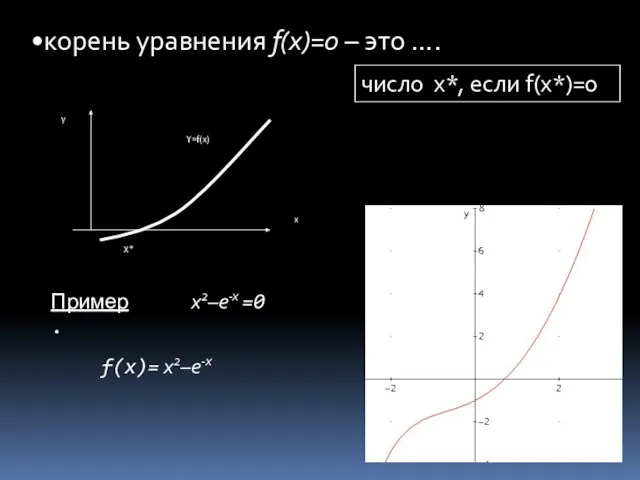
- 3. число x*, если f(x*)=0 корень уравнения f(x)=0 – это …. x2–e-x =0 Пример. f(x)= x2–e-x
- 4. корень k-й кратности уравнения f(x)=0 – это число x*, если при x=x* вместе с функцией f(x)
- 5. число x , если |x-x*| приближенное значение корня уравнения f(x)=0 с погрешностью e
- 6. Этапы решения нелинейного уравнения f(x)=0: 1 Постановка задачи 2 Отделение корня 3 Уточнение корня 4 Анализ
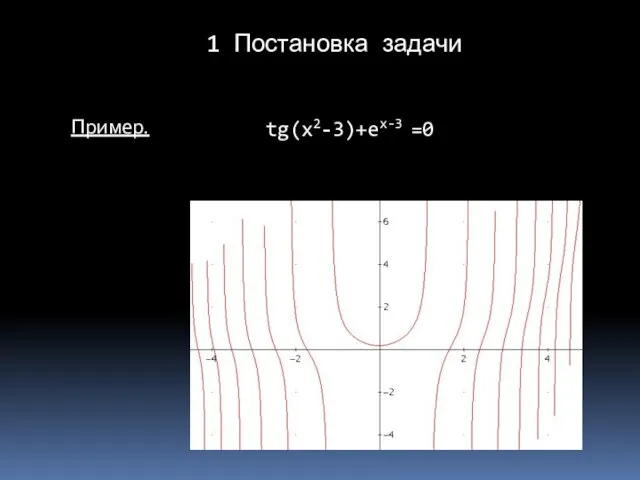
- 7. Пример. tg(x2-3)+ex-3 =0 1 Постановка задачи
- 8. Определение числа корней алгебраических уравнений Пример: Общее число корней : число положительных корней : число отрицательных
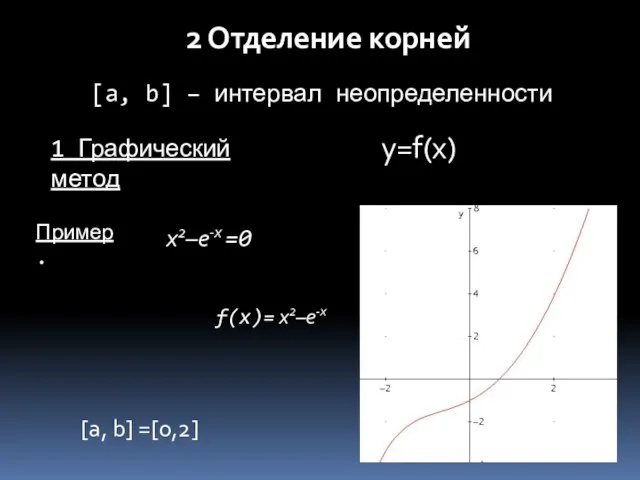
- 9. 2 Отделение корней 1 Графический метод y=f(x) x2–e-x =0 Пример. f(x)= x2–e-x [a, b] – интервал
- 10. f(x)=0 f1(x)=f2(x) y=f1(x) y=f2(x) x2–e-x =0 Пример. y=f1(x)= x2 y=f2(x)= e-x графический метод: [a, b] =[0,2]
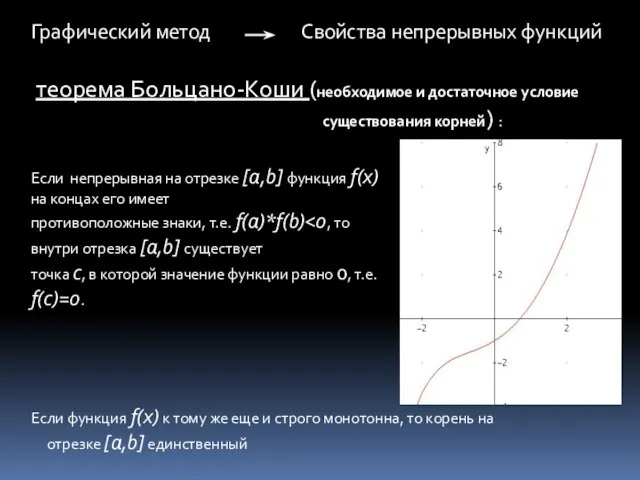
- 11. теорема Больцано-Коши (необходимое и достаточное условие существования корней) : Свойства непрерывных функций Если непрерывная на отрезке
- 12. 2 Отделение корней 2.2 Аналитический Метод Штурма Критические точки функции f(x) – это … точки, в
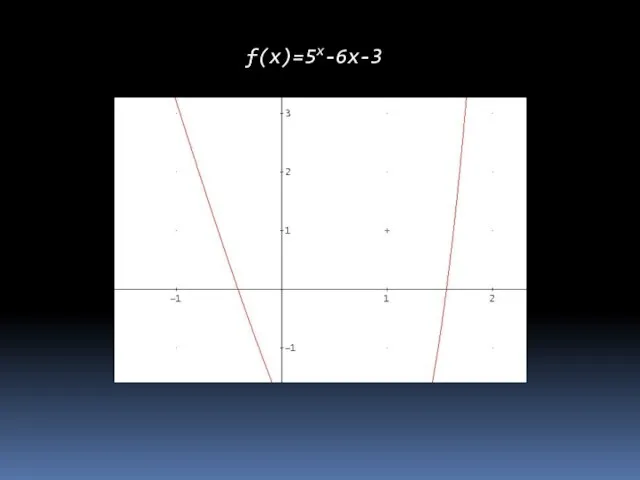
- 13. f(x)=5x-6x-3
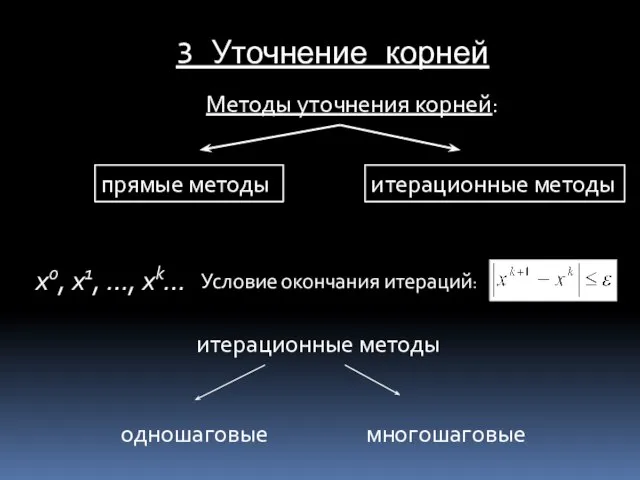
- 14. 3 Уточнение корней Методы уточнения корней: прямые методы итерационные методы одношаговые многошаговые x0, x1, …, xk…
- 15. 3 Методы уточнения корней 1 перебор всех возможных значений функции 2 замена нелинейной функции той или
- 16. Как найти общее число корней алгебраического уравнения? Контрольные вопросы: 2) Что дает отделение корней? 3) Какие
- 17. Тест: 2 Корень уравнения называется простым, если А) это простое число Б) он однократный В) он
- 18. 4 Критические точки функции f(x) – это точки, в которых А) функция f(x) равна нулю или
- 20. Скачать презентацию





![f(x)=0 f1(x)=f2(x) y=f1(x) y=f2(x) x2–e-x =0 Пример. y=f1(x)= x2 y=f2(x)= e-x графический метод: [a, b] =[0,2]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/890612/slide-9.jpg)





 Квадратный корень из степени
Квадратный корень из степени Определение свойств функции по графику
Определение свойств функции по графику Параллельные прямые, перпендикулярные к плоскости
Параллельные прямые, перпендикулярные к плоскости Основы математической статистики. Регрессионный и корреляционный анализы
Основы математической статистики. Регрессионный и корреляционный анализы Задача о кратчайшем пути
Задача о кратчайшем пути Развертка. Создание объёмных фигур из плоскости
Развертка. Создание объёмных фигур из плоскости Перетворення графіків
Перетворення графіків Идеально сбалансированное дерево. Задание
Идеально сбалансированное дерево. Задание Больше, меньше, столько же
Больше, меньше, столько же Геометрические тела. Обьём прямоугольного параллелепипеда. 5 класс
Геометрические тела. Обьём прямоугольного параллелепипеда. 5 класс Формирование действия моделирования через решение текстовых задач
Формирование действия моделирования через решение текстовых задач Уравнение окружности и прямой
Уравнение окружности и прямой Мир чисел
Мир чисел Симмертия. Зеркальное отражение – симметрия
Симмертия. Зеркальное отражение – симметрия Деление дробей
Деление дробей Соста числа 11
Соста числа 11 Деление десятичных дробей
Деление десятичных дробей Квадрат. Основные свойства квадрата
Квадрат. Основные свойства квадрата Сравнение и измерение отрезков
Сравнение и измерение отрезков Стандартный вид одночлена
Стандартный вид одночлена Презентация на тему Решение иррациональных неравенств (11 класс)
Презентация на тему Решение иррациональных неравенств (11 класс)  Презентация на тему КВАДРАТИЧНАЯ ФУНКЦИЯ И КВАДРАТИЧНЫЕ НЕРАВЕНСТВА
Презентация на тему КВАДРАТИЧНАЯ ФУНКЦИЯ И КВАДРАТИЧНЫЕ НЕРАВЕНСТВА  Домашнее задание по геометрии
Домашнее задание по геометрии Количество делителей числа
Количество делителей числа Комплексные числа
Комплексные числа Цифра 1. Посчитаем до 10
Цифра 1. Посчитаем до 10 Презентация по математике "Алгоритмы внутренних точек с приближенным решением вспомогательной задачи" -
Презентация по математике "Алгоритмы внутренних точек с приближенным решением вспомогательной задачи" -  Algorytmy i struktury danych
Algorytmy i struktury danych